r. akad. 1997/98	L A B O R A T O R I U M Z F I Z Y K I
nr ćwicz. 50	Pochłanianie światła
wydział: elektroniczny kierunek: elektronika i telekomunikacja grupa: I	imię i nazwisko: Krzysztof Górski Krzysztof Granda
data wykonania:	ocena		data zaliczenia	podpis
08.12.1997	teoria
		sprawozdanie

1. Zasada pomiaru

Absorpcją światła, czyli pochłanianiem, nazywamy straty energii strumienia światła, występujące przy przechodzeniu tego strumienia przez ośrodek materialny, w którym to światło nie ulega rozproszeniu. Straty strumienia świetlnego w substancji są wynikiem przemiany energii strumienia świetlnego w różne rodzaje energii wewnętrznej substancji (np. ciepło, jonizacja) oraz w energię promieniowania wtórnego, wysyłanego w innych kierunkach lub mającego inny skład widmowy.

Gdy przez warstwę dx jednorodnego, przezroczystego ośrodka przechodzi w kierunku x wiązka światła monochromatycznego, to osłabienie strumienia świetlnego dΦ na drodze dx jest proporcjonalne do wartości tego strumienia i grubości warstwy.

a więc,

(1)

gdzie k - współczynnik absorpcji, jest wielkością charakteryzującą absorpcyjne własności ośrodka.

Jeśli strumień światła przechodzi przez warstwę o skończonej grubości l i zmienia się od wartości początkowej Φ₀ do wartości końcowej Φ_l , to całkując równanie różniczkowe (1) w tych granicach otrzymamy:

lnΦ_l - lnΦ₀ = - k⋅l (2)

czyli

(3)

Zależność tę nazywamy prawem Lamberta - Beera. Sens fizyczny współczynnika absorpcji k wynika bezpośrednio ze wzoru (3).

Dla ,
zatem odwrotność współczynnika absorpcji k określa taką drogę w ośrodku, po przejściu której strumień światła zmaleje e razy.

W układzie współrzędnych logarytmicznych równanie (2) przedstawia linię prostą.

Stosunek
nazywany jest transmisją T.

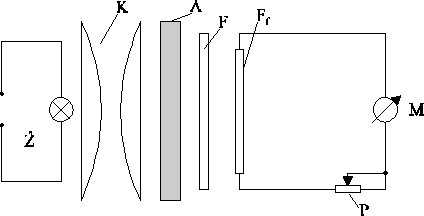
2. Schemat układu pomiarowego

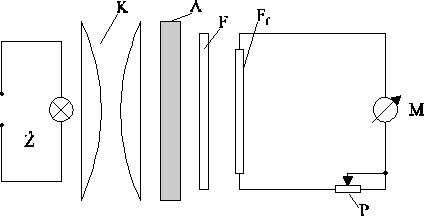
Kolorymetr użyty w pomiarach składa się ze źródła światła Ź, kondensatora K, filtru selektywnego F (komplet filtrów), fotodiody lub fotoogniwa F_f, połączonego z miernikiem M przez potencjometr P. Badane płytki szklane A umieszcza się na drodze wiązki światła w specjalnej komorze, prostopadle do wiązki. Miernik kolorymetru ma dwie skale - skalę transmisji i absorpcji. Skala transmisji podaje w procentach wartość stosunku

gdy bez absorbenta strumień Φ₀ spowoduje pełne wychylenie wskazówki miernika (100%). Do regulacji tego wskaźnika służy potencjometr P.

3. Ocena dokładności pojedynczych pomiarów

W doświadczeniu użyto:

1. Kolorymetru do pomiaru transmisji T ΔT = 0.5%

2. Śruba mikrometryczna do pomiaru d Δd = 0.01 [mm]

4. Tabele pomiarowe

TABELA 1

Rodzaj płytek	Filtr [nm]	d [mm]	lnT
			1d	2d	3d	4d	5d
Przezroczyste	474	2,85	-0,083	-0,174	-0,261	-0,342	-0,431
Przezroczyste	555	2,85	-0,084	-0,163	-0,236	-0,329	-0,400
Przezroczyste	608	2,85	-0,105	-0,186	-0,261	-0,357	-0,446
Przezroczyste	636	2,85	-0,094	-0,205	-0,315	-0,431	-0,545
Przezroczyste	670	2,85	-0,673	-0,844	-0,942	-1,079	-1,171
Zielone	474	2,19	-1,109	-2,207	-3,219	-4,605	-5,298
Zielone	555	2,19	-1,273	-2,408	-3,507	-4,605	-5,298
Zielone	608	2,19	-2,303	-4,605	-	-	-
Zielone	636	2,19	-3,219	-4,605	-	-	-
Zielone	670	2,19	-	-	-	-	-
Brązowe	474	2,60	-2,813	-4,605	-	-	-
Brązowe	555	2,60	-1,309	-2,813	-3,912	-4,605	-
Brązowe	608	2,60	-0,968	-1,897	-2,813	-3,507	-
Brązowe	636	2,60	-1,609	-2,526	-3,219	-3,912	-
Brązowe	670	2,60	-0,713	-1,470	-2,207	-2,996	-

5. Przykładowe obliczenia wyników pomiarów wielkości złożonej

- obliczenie współczynnika absorpcji ze wzoru:

Przykładowe obliczenie współczynnika k dla pomiaru nr 1 z tabeli 1:

Zestawienie współczynników k

	Przezroczysta	Zielona	Brązowa
kλ1	0,03	0,48	0,69
kλ2	0,03	0,46	0,42
kλ3	0,03	1,05	0,33
kλ4	0,04	0,63	0,30
kλ5	0,03	-	0,29

6. Rachunek błędów

Błąd współczynnika absorpcji obliczono metodą różniczki zupełnej

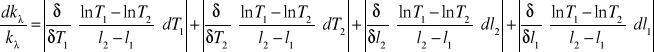
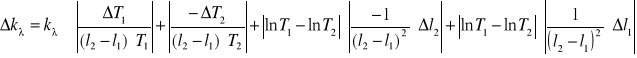
przy czym: l₁, l₂ - grubości płytek

Δl₁, Δl₂ - błędy pomiaru grubości płytek

- Przykładowe obliczenie dla danych zawartych w tabeli 1, pozycja nr 1:

ΔT₁ = ΔT₂ = 0,005 T₁ = 92% = 0,92 T₂ = 65% = 0,65

lnT₁ = - 0,083 lnT₂ = - 0,431 d₁ = 2,85 [mm] d₂ = 14,25 [mm]

Δd₁ = 0,01 [mm] Δd₂ = 0,05 [mm]

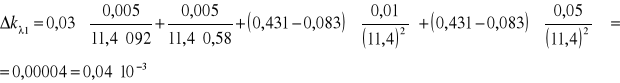
Tabela błędów współczynnika

	Przezroczysta	Zielona	Brązowa
Δkλ1	0,04 ⋅ 10^-3	57,20 ⋅ 10^-3	165,78 ⋅ 10^-3
Δkλ2	0,04 ⋅ 10^-3	54,90 ⋅ 10^-3	29,28 ⋅ 10^-3
Δkλ3	0,04 ⋅ 10^-3	293,94 ⋅ 10^-3	8,44 ⋅ 10^-3
Δkλ4	0,06 ⋅ 10^-3	190,72 ⋅ 10^-3	11,26 ⋅ 10^-3
Δkλ5	0,1 ⋅ 10^-3	-	4,75 ⋅ 10^-3

7. Zestawienie wyników pomiarów

	Przezroczysta	Zielona	Brązowa
kλ1	(30,00 ± 0,04) ⋅ 10^-3	(480,00 ± 57,20) ⋅ 10^-3	(690,00 ± 165,78) ⋅ 10^-3
kλ2	(30,00 ± 0,04) ⋅ 10^-3	(460,00 ± 54,90) ⋅ 10^-3	(420,00 ± 29,28) ⋅ 10^-3
kλ3	(30,00 ± 0,04) ⋅ 10^-3	(1050 ± 293,94) ⋅ 10^-3	(330,00 ± 8,44) ⋅ 10^-3
kλ4	(40,00 ± 0,04) ⋅ 10^-3	(630,00 ± 109,72) ⋅ 10^-3	(300,00 ± 11,26) ⋅ 10^-3
kλ5	(40,00 ± 0,04) ⋅ 10^-3	-	(290,00 ± 4,75) ⋅ 10^-3

8. Uwagi i wnioski

Podczas wykonywania ćwiczenia największy wpływ na niedokładność pomiarów i różnice wyników mogły mieć zabrudzone i porysowane płytki oraz niedokładność pomiaru grubości płytek, ponieważ mikrometr po skręceniu wskazywał 0,1 mm. Największy jednak wpływ na odczyt wyników pomiaru miał sam obserwator, którego zadaniem było odczytać wynik transmisji i zmierzyć grubość płytek.

---