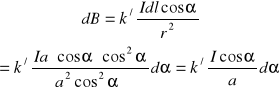Wykład 20
Pole magnetyczne
Pole magnetyczne. Wektor indukcji magnetycznej. Siła Lorentza
Do XIX - go wieku pod nazwą magnetyzm rozumieli zbiór zjawisk, związanych głownie ze zdolnością pewnych minerałów (magnetyków) przyciągać kawałki żelaza. W starożytności było zauważone, że Ziemia też posiada właściwości magnetyczne i właśnie to odkrycie dało możliwość zbudować kompas.
W roku 1820 Oersted jako pierwszy odkrył, że prąd płynący w przewodzie może wywoływać efekty magnetyczne podobne do efektów które wywołują minerały magnetyczne. Na przykład prąd płynący w przewodniku może zmieniać orientację igły kompasu. Jeżeli wyłączymy prąd, przewodnik traci swoje właściwości magnetyczne. Prąd elektryczny jest związany z uporządkowanym ruchem ładunków, a zatem łatwo dojść do wniosku, że zjawiska magnetyczne są związane z ruchem (makroskopowym, uporządkowanym) ładunków elektrycznych. Ampère na podstawie podobnych rozumowań doszedł do wniosku, że właściwości magnetyczne minerałów magnetycznych muszą również być związane z wewnętrznymi prądami molekularnymi, które istnieją w tych minerałach.
Ponieważ przewodnik z prądem wykazuje swoje właściwości magnetyczne w dowolnym punkcie z otoczenia przewodnika, mówimy, że prąd elektryczny wytwarza w otaczającej przewodnik przestrzeni pole magnetyczne . Podstawową charakterystyką pola magnetycznego stanowi wektor indukcji magnetycznej ![]()
. Ten wektor, podobnie jak wektor natężenia pola elektrycznego, możemy określić mierząc siłę z którą pole magnetyczne działa na przykład na igłę kompasu. Okazało się, że pole magnetyczne nie działa na nieruchome ładunki elektryczne.
|
Z doświadczeń natomiast wynika, że na ładunek elektryczny
|
Siła ![]()
jest zawsze skierowana prostopadle do prędkości ![]()
ładunku, a więc 1) ta siła nie może zmienić wielkości bezwzględnej prędkości ładunku, a jedynie zmienia jej kierunek; 2) siła ![]()
nie wykonuje pracy ponieważ ![]()
.
Jeżeli w miejscu gdzie znajduje się ładunek, oprócz pola magnetycznego istnieje pole elektryczne o natężeniu ![]()
, siła z którą działają na ładunek pole elektryczne i pole magnetyczne jest równa
![]()
. (XX.2)
Siłę ![]()
nazywamy siłą Lorentza. Pierwszy człon we wzorze (XX.2) (![]()
) nazywa się elektryczną składową siły Lorentza, drugi wyraz zaś (![]()
) nazywa się magnetyczną składową siły Lorentza.
Pole magnetyczne poruszającego się ładunki elektrycznego. Prawo Biota - Savarta
Z doświadczeń wynika, że poruszający się z prędkością ![]()
(![]()
, gdzie ![]()
- prędkość światła w próżni) ładunek elektryczny ![]()
wytwarza w dowolnym punkcie ![]()
pole magnetyczne o indukcji
![]()
. (XX.3)
Tu ![]()
jest wektorem określającym położenie punktu ![]()
. Początek wektora ![]()
pokrywa się z punktem, gdzie znajduje się ładunek ![]()
. Współczynnik ![]()
zależy od stosowego układu jednostek.
Pole magnetyczne poruszającego się ładunku zależy w każdym punkcie przestrzeni od czasu, ponieważ podczas ruchu ładunku zmienia się wartość i kierunek wektora ![]()
.
Korzystając ze wzoru (XX.3) łatwo obliczyć indukcję pola magnetycznego, wytwarzanego przez mały odcinek ![]()
przewodnika, w którym płynie prąd ![]()
.
|
Zgodnie ze wzorem (XIX.4) gęstość prądu jest równa
gdzie
Wielkość |
![]()
. (XX.5)
Pomnóżmy obie strony równania (XX.5) przez objętość ![]()
elementu ![]()
przewodnika
![]()
. (XX.6)
Tutaj uwzględniliśmy, że ![]()
jest ładunkiem ![]()
elementu objętości ![]()
.
Podstawiając do wzoru (XX.7) człon ![]()
zamiast ![]()
otrzymujemy
![]()
. (XX.7)
Wprowadźmy wektor ![]()
, którego moduł równa się długości elementu ![]()
przewodnika, a kierunek pokrywa się z kierunkiem prądu elektrycznego. Ponieważ
![]()
, (XX.8)
ze wzoru (XX.7) znajdujemy
![]()
. (XX.9)
Wzory (XX.7) i (XX.9) są znane jako prawo Biota - Savarta. Prawo Biota - Sawarta daje możliwość znaleźć indukcję ![]()
pola magnetycznego prądu, płynącego w przewodniku o skończonych wymiarach i dowolnym kształcie.
Zasada superpozycji pól magnetycznych
Zasada superpozycji pól magnetycznych odgrywa bardzo ważną role przy obliczeniu pola magnetycznego. Zgodnie z zasadą superpozycji pól magnetycznych indukcja ![]()
w dowolnym punkcie pola magnetycznego przewodnika, przez który przepływa prąd ![]()
, równa się sumie wektorowej indukcji ![]()
, elementarnych pól magnetycznych wytwarzanych przez poszczególne odcinki ![]()
tego przewodnika
![]()
. (XX.10)
Jeżeli będziemy powiększać w sposób nieograniczony liczbę ![]()
odcinków, to w granice ![]()
ze wzoru (XX.10) otrzymujemy
![]()
. (XX.11)
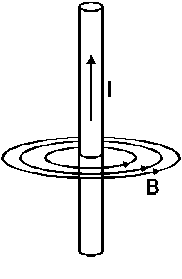
Jako przykład zastosowania prawa Biota-Savarta oraz zasady superpozycji pól magnetycznych, znajdziemy pole magnetyczne nieskończenie długiego przewodnika wzdłuż którego płynie prąd o natężeniu ![]()
. Zgodnie ze wzorem (XX.9) pole magnetyczne dowolnego odcinka ![]()
przewodnika jest prostopadłe do płaszczyzny rysunku, a zatem sumowanie wektorowe ![]()
możemy zamienić sumowaniem ich moduły. Z rysunku wynika, że
|
gdzie
|
Całkując wzór (XX.13) od ![]()
do ![]()
otrzymujemy
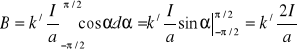
. (XX.14)
Linii pola magnetycznego i prawo Gaussa dla pola magnetycznego
Pole magnetyczne możemy, podobnie do pola elektrycznego, prezentować graficznie rysując tzw. linie pola magnetycznego czyli linie wektora indukcji magnetycznej. Na rysunku pokazane są linie pola magnetycznego wokół prostoliniowego przewodnika z prądem. Linie pola ![]()
wytwarzanego przez przewodnik są zamkniętymi współśrodkowymi okręgami w płaszczyźnie prostopadłej do przewodnika. Wektor ![]()
jest styczny do tych linii pola w każdym punkcie. To, że linie pola ![]()
są zamknięte stanowi fundamentalną różnicę między polem magnetycznym i elektrycznym, którego linie zaczynają się i kończą na ładunkach. Zamkniętość linii pola magnetycznego jest wynikiem faktu, że w przyrodzie nie występują "ładunki" magnetyczne.
Z faktu, że linie indukcji dowolnego pola magnetycznego tworzą krzywe zamknięte wynika, że strumień ![]()
pola magnetycznego przez dowolną powierzchnię zamkniętą równa się zeru
|
Istotnie ponieważ linie pola magnetycznego są zamknięte ilość linii pola wchodzących do obszaru ograniczonego powierzchnia |
Skorzystajmy teraz z twierdzeniem Gaussa - Ostrogradskiego
![]()
. (XX.16)
Tu ![]()
- dowolne pole wektorowe.
Biorąc pod uwagę wzór (XX.16) ze wzoru (XX.15) otrzymujemy
![]()
. (XX.17)
Skąd
![]()
. (XX.18)
Wzory (XX.15) i (XX.18) wyrażają prawo Gaussa dla pola magnetycznego.
Cyrkulacja pola wektora ![]()
. Wirowy charakter pola magnetycznego. Prawo Ampère'a
|
Rozważmy nieskończenie długi przewodnik wzdłuż którego płynie prąd |
Wektor ![]()
jest styczny do tej linii pola w każdym punkcie i wynosi, zgodnie z (XX.14)
![]()
. (XX.19)
Obliczymy teraz całkę okrężną z wektora ![]()
wzdłuż okręgu o promieniu ![]()
(cyrkulację wektora ![]()
)
![]()
. (XX.20)
Widzimy, że cyrkulacja (krążenie) wektora ![]()
nie zależy od promienia ![]()
, a zależy jedynie od natężenia prądu, który przepływa przez powierzchnie rozpiętej na obwodzie ![]()
.
W elektrostatyce udowodniliśmy, że dla pola elektrostatycznego, które jest polem potencjalnym, cyrkulacja natężenia pola elektrycznego jest równa zeru (patrz wzór (XVI.31)
![]()
. (XX.21)
Ze wzoru (XX.20) wynika, że pole magnetyczne nie jest polem potencjalnym, a zatem nie możemy dla niego wprowadzić skalarną funkcję potencjalną.
Pole, dla którego cyrkulacja wektora natężenia pola nie równa się zeru, nosi nazwę pola wirowego. Więc pole magnetyczne, w odróżnieniu od pola elektrostatycznego, jest polem wirowym, a nie potencjalnym.
|
Można wykazać, że wzór (XX.20) jest słuszny dla dowolnego obwodu
Tu przez |
W równaniu (XX.22) prąd ![]()
![]()
-ego przewodnika przyjmuje się jako dodatni, jeżeli z końca wektora gęstości prądu, którego kierunek pokrywa się z osią przewodnika, a zwrot odpowiada zwrotowi prądu, obieg obwodu ![]()
widoczny jest jako zachodzący w kierunku przeciwnym do kierunku ruchu wskazówki zegara (reguła korkociągu). W przypadku przeciwnego kierunku obiegu ![]()
lub przeciwnego kierunku prądu w przewodniku prąd ![]()
przyjmuje się jako prąd ujemny. Wzór (XX.22) wyraża tak zwane prawo Ampère albo prawo przepływu prądu.
Rotacja wektora ![]()
. Twierdzenie Stokesa
Rozważmy cyrkulację z dowolnego pola wektorowego ![]()
![]()
.
|
Prowadźmy teraz dowolną krzywą
|
Istotnie przy całkowaniu po ![]()
i ![]()
poruszamy się w przeciwnych kierunkach wzdłuż krzywej ![]()
a zatem ![]()
.
Tworząc dalej w ten sam sposób szereg zamkniętych konturów ![]()
otrzymujemy
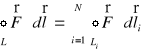
. (XX.23)
|
Wybierzmy przy dość dużym
|
Okazuje się, że graniczna wartość stosunku ![]()
do pola ![]()
zachowuje się tak samo jak rzut wektora na kierunek określony jednostkowym wektorem ![]()
. Wektor ten nazywa się rotacją wektora ![]()
i oznacza się symbolem ![]()
. A zatem
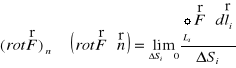
. (XX.24)
|
Dla tego żeby znaleźć składowe wektora |
Oznaczmy przez ![]()
i ![]()
średnie wartości składowej ![]()
na odcinkach 1 i 3, a przez ![]()
i ![]()
- średnie wartości składowej ![]()
na odcinkach 2 i 4. Wtedy dla cyrkulacji wektora ![]()
wzdłuż obwodu ![]()
możemy zapisać
![]()
. (XX.25)
Jeżeli prostokąt jest mały, to dla składowych ![]()
możemy w dobrym przybliżeniu zapisać
![]()
, ![]()
(XX.26)
W podobny sposób dla składowych ![]()
możemy zapisać
![]()
, ![]()
. (XX.27)
Po podstawieniu (XX.26) i (XX.27) do wzoru (XX.25) znajdujemy
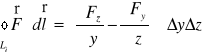
. (XX.28)
Dzieląc cyrkulację (XX.28) przez ![]()
znajdujemy zgodnie z (XX.24) ![]()
- składową wektora ![]()
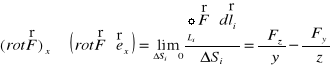
. (XX.29)
Postępując w podobny sposób znajdujemy dla ![]()
i ![]()
- składowych wektora ![]()
następujące wzory
![]()
, (XX.30)
![]()
, (XX.31)
Biorąc pod uwagę wzory (XX.29) - (XX.31), wektor ![]()
możemy zapisać w postaci
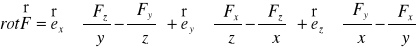
, (XX.32)
gdzie ![]()
są jednostkowymi wektorami wzdłuż osi ![]()
.
Wprowadzając operator nabla (patrz Wykład 16, wzór (XVI.7))
![]()
,
wzór (XX.32) możemy zapisać w postaci
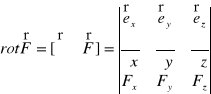
. (XX.33)
Powróćmy teraz do równania (XX.23) i zapiszmy to równanie w postaci
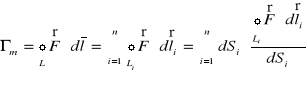
. (XX.34)
W granice ![]()
i ![]()
nieskończenie mała pole ![]()
przechodzi w ![]()
, wyraz w nawiasach staje się (![]()
), suma zaś przechodzi a całkę powierzchniową po powierzchni ![]()
rozpiętej na krzywej ![]()
![]()
. (XX.35)
Twierdzenie (XX.35) nosi nazwę twierdzenia Stokesa.
Różniczkowa postać prawa Ampère'a
Zastosujemy teraz twierdzenie Stokesa do pola magnetycznego ![]()
. Całkowity prąd ![]()
płynący przez powierzchnie rozpiętą na krzywej ![]()
możemy wyrazić jako całkę powierzchniową z gęstości prądu ![]()
![]()
. (XX.36)
Podstawiając (XX.36) do prawa Ampère'a (XX.22)
![]()
. (XX.37)
Porównując (XX.37) z twierdzeniem Stokesa (XX.35) otrzymujemy różniczkową (lokalną) postać prawa Ampème'a.
Na zakończenie porównujemy różniczkowe równania dla pola magnetycznego i pola elektrostatycznego w próżni:
![]()
, ![]()
;
![]()
, ![]()
.
W ostatnim równaniu stała ![]()
4![]()
·10 - 7 N/A2 nazywa się stałą magnetyczną albo przenikalnością magnetyczną próżni.
68
Wyszukiwarka
Podobne podstrony:
ćw.20, Fizyka, Skrypt do Laborek
20 Fizyka
2010 01 20 fizyka
cw-20, Fizyka laboratorium, Sprawozdania
fiza 20, Fizyka
20 Fizyka jądrowaid 21351 ppt
Fizyka wykład dajzeta 20 02 2011
Fizyka wykład dajzeta 20 03 2011
Fizyka wykład dajzeta 20 02 2011
Fizyka 0 wyklad organizacyjny Informatyka Wrzesien 30 2012
Zal-lab-BP-zaoczne, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
kolokwium 14 01 10, polibuda, 3 semestr, fizyka i inżynieria materiałowa (kolokwia, sprawozdania, w
test-B, politechnika lubelska, budownictwo, 3 rok, semestr 5, fizyka budowli, wykład
więcej podobnych podstron