LABORATORIUM FIZYCZNE
Ćwiczenie C2 Wyznaczanie stosunku Cp /Cv dla powietrza metodą Clementa i Desormesa.
Gortak Małgorzata Krysiuk Krzysztof			DSZ-PC1 Gr.2
16.03.2006		Ocena:

1. Wstęp teoretyczny.

W naszym doświadczeniu celu wyznaczenia κ gaz poddajemy trzem przemianom przedstawionym na wykresie. W balonie szklanym znajduje się powietrze pod ciśnieniem atmosferycznym p₀. Za pomocą pompki zwiększamy ciśnienie do p₀+ p₁ (stan I na wykresie). Otwierając na kilka sekund zawór K₂ łączący balon z powietrzem atmosferycznym powodujemy adiabatyczne rozprężanie gazu. Na wykresie jest to przejście od stanu I do stanu II. Korzystając z równania adiabaty, otrzymujemy:

po przekształceniu:

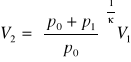
Wskutek rozprężania adiabatycznego temperatura gazu w balonie obniża się gdyż praca rozprężania odbywa się kosztem obniżenia energii wewnętrznej gazu. Po kilku sekundach, gdy ciśnienie w balonie zrówna się z ciśnieniem atmosferycznym p_0, zamykamy zawór K₂. gaz powoli ogrzewa się do temperatury otoczenia. Wskutek tego ciśnienie wzrasta do p₀+ p₂ (przemiana izochoryczna), co przedstawia prosta II - III na wykresie. Temperatury w punktach I i III są jednakowe (temperatura otoczenia). Zatem przejścia ze stanu I do III można dokonać na drodze przemiany izotermicznej.

Przemiany gazowe zachodzące w układzie do wyznaczania współczynnika adiabaty κ powietrza metodą Clementa i Desormesa.

Korzystając z prawa Boyle'a - Mariotte'a, otrzymamy:

co po kolejnych przekształceniach daje nam:

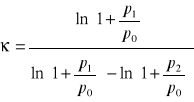
W warunkach eksperymentu p₁/p₀<<1 oraz p₂/p₀<<1. Rozwijając logarytm w szereg możemy, więc ograniczyć się tylko do pierwszego wyrazu rozwinięcia:

W manometrze cieczowym p= ρ x g x h, gdzie ρ - gęstość cieczy, g - przyspieszenie ziemskie, h - różnica wysokości słupków cieczy w ramionach U-rurki. Możemy, więc zapisać:

Aby wyznaczyć κ należy zmierzyć tylko wskazania manometru tylko wskazania manometru h₁ i h₂.

Schemat układu do pomiaru współczynnika adiabaty κ

2. Wykonanie obliczeń do ćwiczenia:

• Obliczenie różnicy poziomu h ₁- h ₂ oraz współczynnika adiabaty κ ze wzoru

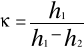
zawarto w tabeli

• Obliczenie wartości średniej arytmetycznej κ_śr:

• Obliczenie odchyleń poszczególnych wartości κ od κ_śr:

Δκ - bezwzględna wartość odchyleń

Δκ ₁=κ _śr -κ ₁ =0,004

Δκ ₂=κ _śr -κ ₂ =0,006

Δκ ₃=κ _śr -κ ₃ =0,006

Δκ ₄=κ _śr -κ ₄ =0,014

Δκ ₅=κ _śr -κ ₅ =0,006

Δκ ₆=κ _śr -κ ₆ =0,004

Δκ ₇=κ _śr -κ ₇ =0,004

Δκ ₈=κ _śr -κ ₈ =0,004

Δκ ₉=κ _śr -κ ₉ =0,004

Δκ ₁₀=κ _śr -κ ₁₀ =0,026

• Obliczenie błędu średniej arytmetycznej Δκ_śr:

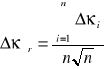
• Obliczenie wartości Δκ metodą różniczki zupełnej dla pomiarów 1, 5, 10:

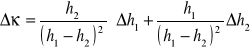
Δh -dokładność pomiaru Δh₁= Δh₂=2mm

• Obliczenie błędu względnego δ:

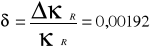
3. Tabela wyników

Nr pomiaru	h1	h2	h1 - h2	κ	κśr	Δκ [10^-3]	Δκśr	Δκśr/κśr
1	19,6	4,5	15,1	1,3	1,304	2,11	0,0025	0,00192
2	19,8	4,7	15,1	1,31
3	19,6	4,7	14,9	1,31
4	19,8	4,5	15,3	1,29
5	19,7	4,7	15	1,31					2,17
6	19,6	4,5	15,1	1,3
7	19,8	4,6	15,2	1,3
8	19,7	4,5	15,2	1,29
9	19,8	4,5	15,3	1,29
10	19,5	4,8	14,7	1,32					2,25

4. Wnioski z przeprowadzonego ćwiczenia:

Przeprowadzane ćwiczenie miało na celu wyznaczenie współczynnika κ. W trakcie przeprowadzania ćwiczenia dało się zauważyć, iż stanowisko badawcze może dostarczyć wielu błędów podczas odczytu pomiarów. Głównie niedokładność opierała się na niedokładności odczytu wysokości słupka cieczy na manometrze.

Wartość stałej adiabaty k odczytywana z tablic fizycznych dla powietrza wynosi k=1,31. Powodem różnicy wyników k_śr i k odczytanego z tablic są właśnie powyższe błędy. Analizując wyniki możemy stwierdzić, że podczas wykonywania ćwiczenia często za późno zamykaliśmy zawór co powodowało niedokładności odczytów i wymagało korekt. Błąd odczytu h₁ i h₂ po ustabilizowaniu się poziomów jest niewielki ( 2mm) i nieznacznie wpływa na wynik.

---