Imię i nazwisko	Ćwiczenie nr 1 Zjawisko Faradaya i pomiar stałej Verdeta
Kierunek i rok Fizyka Mag. Uzup. I	Ocena z kolokwium	Ocena ze sprawozdania	Ocena końcowa
Prowadzący ćwiczenia

Część teoretyczna

Polaryzacja światła (liniowa, kołowa, eliptyczna) i skręcenie płaszczyzn polaryzacji

Światło jest poprzeczną falą elektromagnetyczną. Oko ludzkie i wiele urządzeń optycznych reaguje wyłącznie na pole elektryczne tej fali. Tak więc drgania świetlne możemy uważać za drgania elektryczne i opisywać je równaniem falowym drgań elektrycznych. Zazwyczaj światło jest fala bardzo złożoną, ponieważ występują równocześnie fale o różnych długościach, a drgania zachodzą we wszystkich płaszczyznach przechodzących przez kierunek rozchodzenie się. Celem uproszczenia sytuacji w wielu doświadczeniach stosuje się światło o długościach fal zawartych w bardzo małym przedziale od λ do λ+∆λ. Zakładamy wtedy, że światło o jednej tylko długości fali, czyli monochromatyczne. W niektórych doświadczeniach ograniczamy drgania fali świetlnej do jednej tylko płaszczyzny. Mówimy wtedy, że światło jest spolaryzowane liniowo. Płaszczyzną polaryzacji nazywamy płaszczyznę prostopadłą do płaszczyzny, w której zachodzą drgania. Równanie fali światła monochromatycznego o długości fali λ, spolaryzowanego liniowo w płaszczyźnie wyznaczonej kierunkami z, y przyjmując szczególnie prostą postać

Światło spolaryzowane liniowo otrzymujemy na skutek zjawiska podwójnego załamania, przez odbicie lub wielokrotne załamanie.

Innym sposobem uporządkowania drgań świetlnych jest polaryzacja kołowa lub eliptyczna. W tych przypadkach koniec wektora natężenia pola elektrycznego zakreśla linię śrubową wokół kierunku rozchodzenia się. Polaryzacja kołowa (gdy
) lub polaryzacja eliptyczna (
). Światło spolaryzowane kołowo lub eliptycznie otrzymać możemy przepuszczając światło spolaryzowane liniowo przez cienką płytkę wykonaną z kryształu optycznie czynnego. Światło w płytce rozpada się na wiązkę zwyczajną i nadzwyczajną. Drgania obydwu wiązek zachodzą w wzajemnie prostopadłych płaszczyznach.

Światło spolaryzowane liniowo przechodzące przez niektóre kryształy zwane optycznie czynnymi doznaje skręcenia płaszczyzny polaryzacji. Dzieje się to w kryształach jednoosiowych w przypadku, gdy światło biegnie równolegle do osi optycznej. Kierunek skręcenia płaszczyzny polaryzacji jest różny dla różnych kryształów, a w przypadku kwarcu znamy dwa rodzaje kryształów, z których jedne skręcają płaszczyznę polaryzacji w prawo, a inne w lewo. Zgodnie z teorią Fresnela, skręcenie płaszczyzny polaryzacji tłumaczymy następująco. Światło spolaryzowane liniowo uważać możemy za nałożenie dwóch spójnych kołowo spolaryzowanych drgań, o równych okresach i amplitudach, lecz przeciwnych zwrotach.

Polarymetry

Polarymetr służy do pomiaru skręcenia płaszczyzny polaryzacji światła w substancjach optycznie czynnych. Polarymetr przeznaczony do pomiaru stężenia cukru nazywamy sacharymetrami. Polarymetr składa się ze zwierciadła kierującego światło do przyrządu, filtr przepuszczający wyłącznie światło żółte, polaryzatora, przyrządu półcieniowego zmieniającego płaszczyznę polaryzacji części pola widzenia o niewielki kąt, rurki zawierającej badaną ciecz lub roztwór, analizatora połączonego z kątomierzem oraz lunetki. Przyrząd dodatkowo jest zaopatrzony w lupę zwiększającą dokładność odczytu kąta. Lunetka i lupa mają możliwość dopasowania do ostrości widzenia. Analizator i zwierciadło mogą obrócić się wokół osi optycznej przyrządu. Omówieniu wymaga przyrząd półcieniowy dzieli pole widzenia na części zmieniające nieco płaszczyznę polaryzacji światła w jednej z nich lub w obydwu. Za przyrządem półcieniowym płaszczyzny polaryzacji poszczególnych części wiązki światła tworzą ze sobą niewielki kąt α. Dla uzyskania równego oświetlenia całego pola widzenia przy nieobecności roztworu, analizator ustawiamy w ten sposób, by jego płaszczyzna polaryzacji dzieliła kąt α na dwie równe części. Przyrząd półcieniowy pozwala odczytać położenie płaszczyzny polaryzacji z dokładnością do 0,1
.

Efekt Faradaya i jego fizyczna interpretacja

Ciało przezroczyste umieszczone w polu magnetycznym skręcając płaszczyznę polaryzacji światła, biegnącego równolegle do linii sił pola magnetycznego. Zjawisko to nazywamy zjawiskiem Faradaya. Większość ciał skręca płaszczyznę polaryzacji w kierunku, w którym płynie prąd w uzwojeniach solenoidu. Są jednak i takie ciała, które skręcają płaszczyznę polaryzacji w kierunku przeciwnym. Przy zmianie zwrotu natężenia pola magnetycznego, a więc i kierunku prądu w uzwojeniach solenoidu, zmienia się również kierunek skręcenia płaszczyzny polaryzacji jest proporcjonalny do długości drogi d przebytej w środowisku oraz od indukcji magnetycznej B:

α = ρBd

Współczynnik proporcjonalności ρ nazywamy stałą Verdeta. Indukcję magnetyczną B wytwarzamy za pomocą cewki. Przyjmujemy że wyraża się ona takim wzorem

Pole magnetyczne prądu elektrycznego

Jeśli weźmiemy przewód prostoliniowy z prądem i ustawimy go prostopadle do kartki papieru z nasypanymi piłkami żelaza, to ustawią się one wzdłuż okręgów, podobnie w przypadku cewki linie indukcji wyznaczone przez kierunki opiłków żelaza są liniami zamkniętymi lub też oboma końcami uchodzą do nieskończoności. Tę samą właściwość stwierdza się również wtedy, gdy pole magnetyczne wytwarzają magnesy trwałe: linie indukcji biegną na zewnątrz magnesu od bieguna północnego do bieguna południowego, natomiast wewnątrz magnesu trwałego przebiegają od bieguna południowego do północnego i tworzą w ten sposób linie zamknięte.

Za pomocą prawa Bita - Savarta możemy wyznaczyć natężenie pola magnetycznego pochodzącego od przewodu z prądem. Gdy weźmiemy pod uwagę nie cały przewodnik, lecz jego mały odcinek o długości ∆l. Odcinek ten wygodnie będzie scharakteryzować za pomocą wektora ∆l stycznego do przewodu, a ściślej do linii prądu o zwrocie zgodnym z kierunkiem prądu. Interesuje nas natężenie pola pochodzące od tego elementu przewodu z prądem I w dowolnym punkcie A położenie tego punktu względem naszego elementu ∆l i koniec w punkcie A. Natężenie pola magnetycznego w punkcie A pochodzące od odcinka ∆l (a nie od całego przewodu) wynosi:

Część praktyczna

Przeliczam stopnie sacharymetryczne na stopnie kątowe: 1
S = 0,34613

I [A]	T = 20 C		T = 30 C		T = 40 C		T = 50 C
		α [ S]	stopnie kątowe γ	α [ S]	stopnie kątowe γ	α [ S]	stopnie kątowe γ	α [ S]	stopnie kątowe γ
0,5 1 1,5 2 2,5 3 3,5 4	0,2 0,7 1,2 1,4 1,7 2,3 2,6 3,1	0,069226 0,242291 0,415356 0,484582 0,588421 0,796099 0,899938 1,073003	0,4 0,9 1,1 1,4 1,8 2,3 2,7 2,9	0,138452 0,311517 0,380743 0,484582 0,623034 0,796099 0,934551 1,003777	0,4 0,8 1 1,6 1,9 2,4 2,7 3	0,138452 0,276904 0,34613 0,553808 0,657647 0,830712 0,934551 1,03839	0,5 0,8 1,2 1,4 1,9 2,3 2,6 2,9	0,173065 0,276904 0,415356 0,484582 0,657647 0,796099 0,899938 1,003777

Obliczam indukcję magnetyczną B dla poszczególnych pomiarów obliczam korzystając ze wzoru :

gdzie : μ_o = 4π*10^-7 N/A²

μ_r = 1

N = 900

l_p = 0,4 m

l_s = 0,325 m

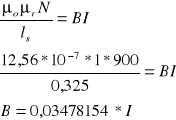
I [A]	B [T]	l * B [m*T]
0,5	0,001739	0,000696
0,8	0,002783	0,001113
1,2	0,004174	0,00167
1,4	0,004869	0,001948
1,9	0,006608	0,002643
2,3	0,008	0,0032
2,6	0,009043	0,003617
2,9	0,010087	0,004035

Metodą regresji liniowej obliczam stałą Verdeta dla poszczególnych temperatur oraz odchylenie standardowe.

gdzie:

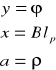
Temp. 20
C

n	x	y	x	y	x y
1	0,000696	0,069226	0,0000004844	0,004792	0,0000481813
2	0,001113	0,242291	0,0000012388	0,058705	0,00026967
3	0,00167	0,415356	0,0000027889	0,172521	0,000693645
4	0,001948	0,484582	0,0000037947	0,23482	0,000943966
5	0,002643	0,588421	0,0000069854	0,346239	0,001555197
6	0,0032	0,796099	0,0000102400	0,633774	0,002547517
7	0,003617	0,899938	0,0000130827	0,809888	0,003255076
8	0,004035	1,073003	0,0000162812	1,151335	0,004329567
	0,018922	4,568916	0,0000548962	3,412074	0,0136428178

= 0,000358042

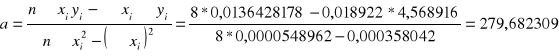
y = 279x + 0,09

y
= 281x + 0,095

y
= 277x + 0,085

Temp. 30
C

n	x	y	x	y	x y
1	0,000696	0,138452	0,0000004844	0,0191689563	0,0000963626
2	0,001113	0,311517	0,0000012388	0,0970428413	0,0003467184
3	0,00167	0,380743	0,0000027889	0,1449652320	0,0006358408
4	0,001948	0,484582	0,0000037947	0,2348197147	0,0009439657
5	0,002643	0,623034	0,0000069854	0,3881713652	0,0016466789
6	0,0032	0,796099	0,0000102400	0,6337736178	0,0025475168
7	0,003617	0,934551	0,0000130827	0,8733855716	0,0033802710
8	0,004035	1,00377	0,0000162812	1,0075542129	0,0040502120
	0,018922	4,672748	0,0000548962	3,3988815118	0,0136475661

= 0,000358042

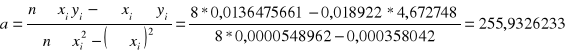
y = 256x + 0,02

y
= 257x + 0,023

y
= 255x + 0,017

Temp. 40
C

n	x	y	x	y	x y
1	0,000696	0,138452	0,0000004844	0,019169	0,0000963626
2	0,001113	0,276904	0,0000012388	0,076676	0,0003081942
3	0,00167	0,34613	0,0000027889	0,119806	0,0005780371
4	0,001948	0,553808	0,0000037947	0,306703	0,0010788180
5	0,002643	0,65764	0,0000069854	0,43249	0,0017381425
6	0,0032	0,830712	0,0000102400	0,690082	0,0026582784
7	0,003617	0,934551	0,0000130827	0,873386	0,0033802710
8	0,004035	1,03839	0,0000162812	1,078254	0,0041899037
	0,018922	4,776587	0,0000548962	3,596566	0,0140280074

= 0,000358042

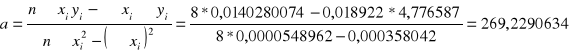
y = 269x + 0,04

y
= 273x + 0,05

y
= 265x + 0,03

Temp. 50
C

n	x	y	x	y	x y
1	0,000696	0,173065	0,0000004844	0,029951494	0,000120453
2	0,001113	0,276904	0,0000012388	0,076675825	0,000308194
3	0,00167	0,415356	0,0000027889	0,172520607	0,000693645
4	0,001948	0,484582	0,0000037947	0,234819715	0,000943966
5	0,002643	0,657647	0,0000069854	0,432499577	0,001738161
6	0,0032	0,796099	0,0000102400	0,633773618	0,002547517
7	0,003617	0,899938	0,0000130827	0,809888404	0,003255076
8	0,004035	1,003777	0,0000162812	1,007568266	0,00405024
	0,018922	4,707368	0,0000548962	3,397697505	0,013657251

= 0,000358042

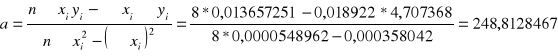
y = 249x + 0,00008

y
= 249,06x + 0,00018

y
= 248,94x - 0,00002

Wnioski

Celem ćwiczenia było badanie zjawiska Faradaya oraz wyznaczenie stałej Verdeta. Stała ta jest zależna od temperatury. Wzrost temperatury powoduje zmniejszenie się stałej, co potwierdzają wyniki doświadczenia i tak

stała wyniosła
;

-
;

-
;

-
.

Wyniki te są obarczone niepewnościami spowodowanymi zarówno niedokładnością przyrządów pomiarowych a także błędami eksperymentatora. Błąd eksperymentatora może polegać na błędzie paralaksy przy odczycie natężenia prądu oraz trudnościami związanymi z odczytam kąta skręcenia.

Wykres dla Temp. 20
C

Wykres dla Temp. 30
C

Wykres dla Temp. 40
C

Wykres dla Temp. 50
C

---