Szeregi liczbowe

1. Wykazać zbieżność szeregów na podstawie definicji :

a)
.

Aby zbadać zbieżność szeregu z definicji , należy sprawdzić , czy istnieje granica ciągu sum częściowych
. Budujemy ciąg sum częściowych :

,
,
, . . . ,
.

Aby zsumować wyrazy w
rozłożymy wyraz ogólny
szeregu na sumę ułamków prostych :

. Stąd mamy
.

Wracając do wyrazu ogólnego ciągu sum częściowych otrzymujemy :

.

Zatem , wracając do definicji zbieżności szeregu , znajdujemy
.

W oparciu o podaną definicję wnioskujemy, że badany szereg jest zbieżny do sumy
.

2. Warunek konieczny zbieżności szeregu : Jeżeli szereg
jest zbieżny , to
.

a)
. Sprawdzamy , czy granica

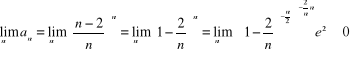
, co oznacza , że szereg nie spełnia warunku koniecznego .

b)
. Obliczamy ( jeśli istnieje ) granicę
:

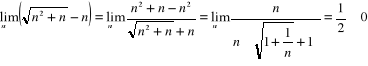
. Badany szereg nie spełnia warunku koniecznego zbieżności szeregu .

3 . Zbadać zbieżność szeregów :

1)
. Korzystamy z kryterium porównawczego . Z nierówności
otrzymujemy nierówność :

. Ponieważ szereg harmoniczny
jest rozbieżny więc z nierówności

i kryterium porównawczego wynika rozbieżność badanego szeregu .

2)
. Prawdziwa jest nierówność :

. Zbadamy zbieżność szeregu
.

Z kryterium Cauchy'ego mamy :
, co oznacza , że szereg
jest zbieżny .

Z nierówności
i na podstawie kryterium porównawczego badany szereg jest także zbieżny .

3)
. Funkcja sinus jest ograniczona , zatem prawdziwa jest nierówność :

.

Ponieważ
to na podstawie kryterium Cauchy'ego szereg
jest zbieżny .

Z nierówności
i kryterium porównawczego szereg
jest zbieżny .

4)
. Podobnie jak wyżej , prawdziwa jest nierówność :

.

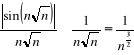
Szereg
jest zbieżny jako harmoniczny rzędu >1 , to z nierówności
na podstawie kryterium porównawczego badany szereg jest zbieżny ( nawet bezwzględnie zbieżny ) .

5)
. Ponieważ
, to prawdziwa jest nierówność

<
.

Szereg
jest zbieżny ( jako harmoniczny rzędu wyższego niż 1 ) więc z nierówności
na podstawie kryterium porównawczego wynika zbieżność badanego szeregu .

6)
. Zauważmy , że

. Szereg
jest zbieżny (jako harmoniczny rzędu drugiego ) . Na podstawie kryterium porównawczego z nierówności
badany szereg jest zbieżny .

7)
. Zauważmy , że szeregi

i
są zbieżne jako geometryczne o ilorazie mniejszym od jeden . Są to szeregi wyrazach dodatnich . Z własności szeregów zbieżnych wynika , że szereg
jest zbieżny i
.

8)
. Przekształcamy wyraz ogólny szeregu :

dla
. Zauważmy , że

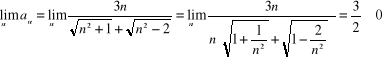
Szereg nie spełnia warunku koniecznego więc jest rozbieżny .

9)
. Z kryterium Cauchy'ego mamy
, co oznacza , że badany szereg jest zbieżny .

10)
. Badamy ten szereg korzystając z kryterium d'Alemberta :

. Oznacza to , że badany szereg jest zbieżny .

11)
. Z kryterium d'Alemberta mamy :

Co oznacza , że szereg jest rozbieżny .

12)
. Korzystamy z kryterium d'Alemberta :

badany szereg jest rozbieżny .

13)
. Prawdziwa jest nierówność :


.

Ponieważ
, to
jest rozbieżny . Z nierówności
na podstawie kryterium porównawczego wynika rozbieżność badanego szeregu .

14)
. Badany szereg jest rozbieżny na podstawie kryterium Cauchy'ego , bo
.

15)
.
Ponieważ
, to na podstawie kryterium Cauchy'ego badany szereg jest zbieżny .

16)
. Analogicznie jak wyżej ,
więc na podstawie kryterium Cauchy'ego wnioskujemy , że badany szereg jest zbieżny .

3