Badanie układów komutacyjnych

2. Badanie kodera.

2.1. Zaprojektować i wykonać układ kodera realizujący operację zgodnie z tabelą 2.1. Tabela 2.1.

Gdzie x = ....1...., y = x

Wyprowadzam równanie wyjścia A wybierając te wiersze, dla których A przyjmuje wartość 0,
a następnie wykreślam te x, dla których pojawiło się 1 w jakimkolwiek z wyznaczonych wierszy. Resztę x dodajemy do siebie otrzymując równanie wyjścia. Działamy analogicznie do B, C oraz D.

Równania wyjścia kodera:

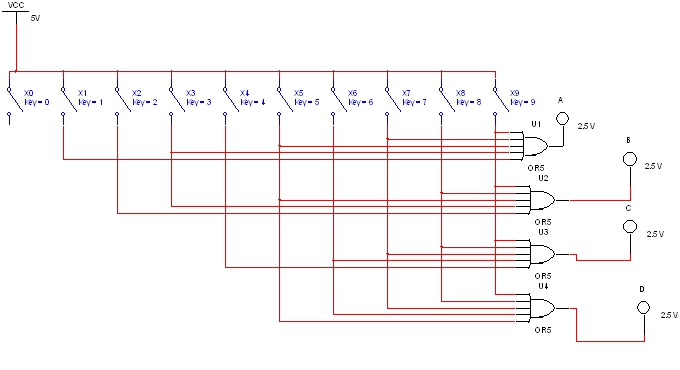
A= x₉+x₇+x₅+x₃+x₁

B= x₉+x₈ x₅+x₃+x₂

C= x₉+x₈+x₇+x₆+x₄

D= x₉+x₈+x₇+x₆+x₅

Układ kodera:

2.3. Zaprojektować i wykonać układ dekodera realizujący operację odwrotną do wykonanego
w pkt. 2.1. kodera.

Tabela 2.3.

D

C

B

A

x9

x8

x7

x6

x5

x4

x3

x2

x1

x0

0

0

0

0

y

y

y

y

y

y

y

y

y

x

0

0

0

1

y

y

y

y

y

y

y

y

x

y

0

0

1

0

y

y

y

y

y

y

y

x

y

y

0

0

1

1

y

y

y

y

y

y

x

y

y

y

0

1

0

0

y

y

y

y

y

x

y

y

y

y

1

0

1

1

y

y

y

y

x

y

y

y

y

y

1

1

0

0

y

y

y

x

y

y

y

y

y

y

1

1

0

1

y

y

x

y

y

y

y

y

y

y

1

1

1

0

y

x

y

y

y

y

y

y

y

y

1

1

1

1

x

y

y

y

y

y

y

y

y

y

Gdzie x = 1, y = 0;

Teraz wejściami są A,B,C i D zaś wyjściami x₀,x₁,...,x₉. Wyprowadzam równanie x0 wybierając wiersz, dla którego x0 przyjmuje wartość 1, a następnie zapisujemy równanie wejść z tego wiersza mnożąc ze sobą każde z wejść. Analogicznie działamy dla pozostałych wyjść.

Układ dekodera: Równania wyjść dekodera:

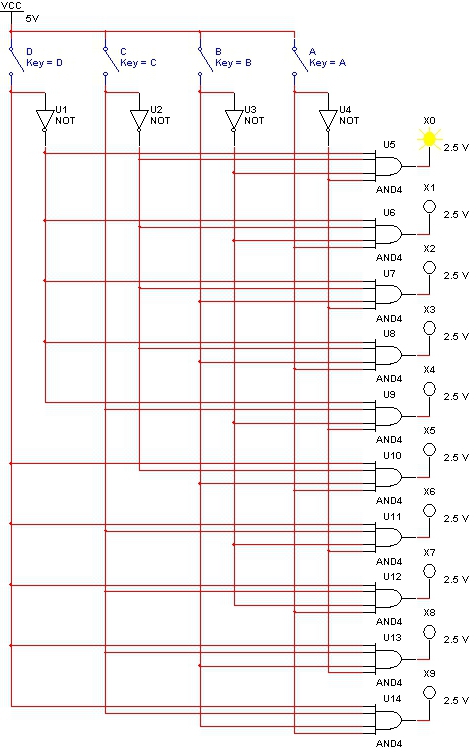
x₀ = A*B*C*D

x₁ = A*B*C*D

x₂ = A*B*C*D

x₃ = A*B*C*D

x₄ = A*B*C*D

x₅ = A*B*C*D

x₆ = A*B*C*D

x₇ = A*B*C*D

x₈ = A*B*C*D

x₉ = A*B*C*D

3. Badanie translatora kodu.

3.1. Zaprojektować i wykonać układ kodera realizujący operację zgodnie z tabelą poniżej.

Tabela 3.1.

x2	x1	x0	D	C	B	A
0	0	0	0	0	0	0
0	0	1	1	0	1	0
0	1	0	0	1	1	0
0	1	1	0	1	0	0
1	0	0	1	1	0	0
1	0	1	0	0	1	1
1	1	0	0	0	0	1
1	1	1	1	0	0	1

Do wyznaczenia A,B,C i D dla sygnałów wejściowych x₂, x₁, x₀ posłużymy się tablicą Karnaugh. Obliczając równanie wyjścia D wpisujemy do tabeli to co D przyjmuje dla odpowiednich kombinacji x₂, x₁, x₀. Analogicznie działamy do pozostałych wyjść, upraszczając równania algebrą Bool'a.

Równania wyjścia translatora:

D

x1x0 x2	00	01	11	10
0	0	1	0	0
1	1	0	1	0

D = x₂*x₁*x₀ + x₂*x₁*x₀ + x₂*x₁*x₀

C

x1x0 x2	00	01	11	10
0	0	0	1	1
1	1	0	0	0

C = x₂*x₁*x₀ + x₂*x₁

B

x1x0 x2	00	01	11	10
0	0	1	0	1
1	0	1	0	0

B = x₁*x₀ + x₂*x₁*x₀

A

x1x0 x2	00	01	11	10
0	0	0	0	0
1	0	1	1	1

A = x₂*x₀ + x₂*x₁ = x₂(x₀ + x₁)

Układ kodera realizujący operacje zgodną z tabelą 3.1:

4.	Badanie multipleksera.

4.2. Wykorzystać multiplekser 74151 do realizacji funkcji logicznej zadanej przez prowadzącego:

Y = [AD(B + C) + B

Rozkładamy funkcję za pomocą drzewka, a następnie na jego podstawie wypełniamy tablicę Karnaugha (tabela 4.1).

Tablica 4.1.

BA DC	00	01	11	10
00	0	0	1	1
01	0	0	1	1
11	0	0	0	1
10	0	1	0	1

Układ z wykorzystaniem multipleksera 74151:

Opisujemy komórki tablicy wartościami sygnałów CBA. Dzięki temu zobaczymy, które komórki odpowiadają odpowiednim wejściom D multipleksera. Każdemu wejściu multipleksera odpowiadają dwie komórki w tabeli. Jeśli obie mają równą wartość od razu podłączamy wejście dla zera - na masę, dla jedynki - na Vcc. Pary, które pozostały uzależniamy od wejścia głównego D. Jeśli komórki w tabeli mają taką samą wartość jak odpowiadający im sygnał D to na to wejście multipleksera podajemy sygnał D, jeśli przeciwny - zaprzeczony D.

BA DC	00	01	11	10
00	0 0	1 0	3 1	2 1
01	4 0	5 0	7 1	6 1
11	4 0	5 0	7 0	6 1
10	0 0	1 1	3 0	2 1

4.4. Zbudować, wykorzystując dwuwejściowe funktory, układ realizujący zadaną przez prowadzącego funkcję.

Minimalizujemy funkcję za pomocą tabeli Karnough (tabela 4.1)

A*B*D*C + B*D + B*A = A*B(C*D) + B(D + A)

x9

x8

x7

x6

x5

x4

x3

x2

x1

x0

D

C

B

A

y

y

y

y

y

y

y

y

y

x

0

0

0

0

y

y

y

y

y

y

y

y

x

y

0

0

0

1

y

y

y

y

y

y

y

x

y

y

0

0

1

0

y

y

y

y

y

y

x

y

y

y

0

0

1

1

y

y

y

y

y

x

y

y

y

y

0

1

0

0

y

y

y

y

x

y

y

y

y

y

1

0

1

1

y

y

y

x

y

y

y

y

y

y

1

1

0

0

y

y

x

y

y

y

y

y

y

y

1

1

0

1

y

x

y

y

y

y

y

y

y

y

1

1

1

0

x

y

y

y

y

y

y

y

y

y

1

1

1

1

---