Pomiary dotyczące obwodów magnetycznych
Pomiar dokonaliśmy przy stałej częstotliwości f = 50 Hz
Obliczam wartość maksymalną (amplitudę) natężenia pola magnetycznego.
![]()
gdzie:
l - średnia droga przepływu strumienia magnetycznego w rdzeniu [m]
I1 - wartość prądu magnesującego [A]
z1 - liczba zwojów uzwojenia magnesującego
l = 2 [m]
z1 = 500
Dla pierwszej wartości I1 = 1,5 [A]
![]()
Dla pozostałych wartości prądu magnesującego obliczam identycznie amplitudę natężenia pola magnetycznego.
Obliczam wartość maksymalną (amplitudę) indukcji magnetycznej wg zależności:
![]()
s - pole przekroju próbki rdzenia [m2]
s = 0,0009 [m2]
z2 - liczba zwojów uzwojenia pomiarowego
z2 = 600
Dla pierwszej wartości U2:
![]()
![]()
Kolejne wartości indukcji dla następnych napięć obliczam analogicznie.
Obliczam przenikalność magnetyczną danego środowiska.
Między amplitudą indukcji magnetycznej a amplitudą natężenia pola magnetycznego istnieje zależność:
![]()
z tego warunku otrzymam:
![]()
dla pierwszego przypadku:
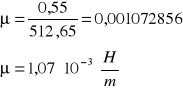
Pozostałe przypadki obliczam analogicznie.
Obliczam przenikalność magnetyczną względną. Korzystam z zależności:
![]()
gdzie:
μo - przenikalność magnetyczna w próżni
μo = 4ּπּ10-7 [H/m]
μ - przenikalność magnetyczna danego środowiska [H/m]
Dla pierwszego przypadku:
![]()
Dla pozostałych przypadków obliczam analogicznie.
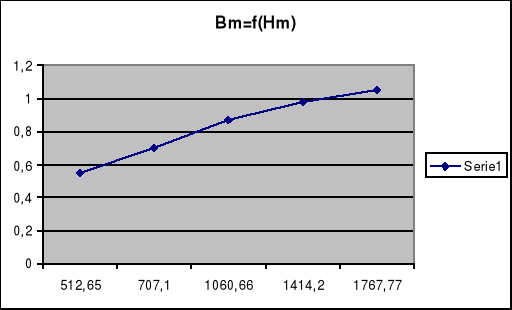
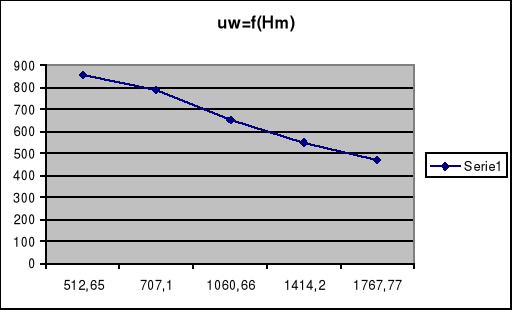
Charakterystyki magnesowania próbki:
Obliczam straty w cewce napięciowej watomierza wynoszą:
![]()
Rn - rezystancja cewki watomierza dołączonej do uzwojenia pomiarowego
Rn = 5 kΩ
Dla pierwszego przypadku U2 = 95,5 V
![]()
Dla pozostałych przypadków obliczenia analogiczne.
Obliczenia strat mocy w cewce woltomierza wg zależności:
![]()
Rv - rezystancja cewki napięciowej woltomierza
Rv = 5 kΩ
Ponieważ zależność jest taka sama jak w punkcie pierwszym, zatem wyniki obliczeń będą takie same.
Obliczenia straty mocy w obwodzie magnetycznym.
![]()
ponieważ Pn = Ph zatem
![]()
gdzie:
z1 - liczba zwojów uzwojenia magnesującego
z2 - liczba zwojów uzwojenia pomiarowego
P - moc wskazana przez watomierz
Dla pierwszej wartości Pn = 1,824 W, z1 = 500, z2 = 600, P = 85 W.
![]()
Dla pozostałych wartości tok obliczeń analogicznych.
Dzielę straty mocy Pm w obwodzie magnetycznym przez masę rdzenia
m = 10 kg i otrzymuję stratność
![]()
Dla pierwszego przypadku Pm = 67,19 W
![]()
Dla pozostałych przypadków obliczenia analogiczne.
5. Obliczenia strat na histerezę.
![]()
czyli
![]()
Pm - straty mocy w obwodzie magnetycznym.
Dla pierwszego przypadku:
![]()
Dla pozostałych przypadków analogicznie.
6. Obliczenia strat na histerezę przypadające na 1kg masy rdzenia.
![]()
gdzie: m = 10kg
![]()
Dla pozostałych przypadków analogicznie.
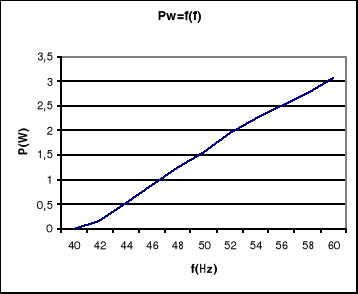
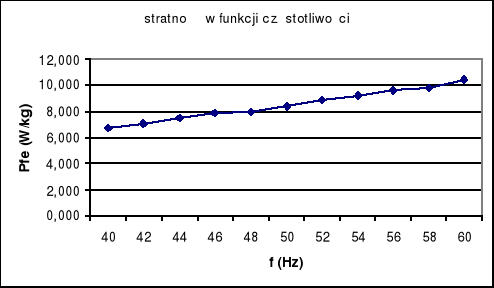
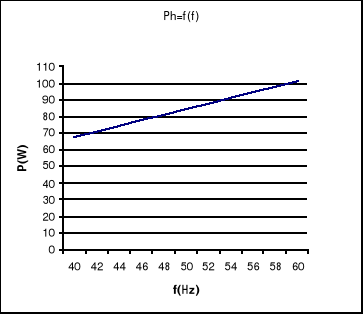
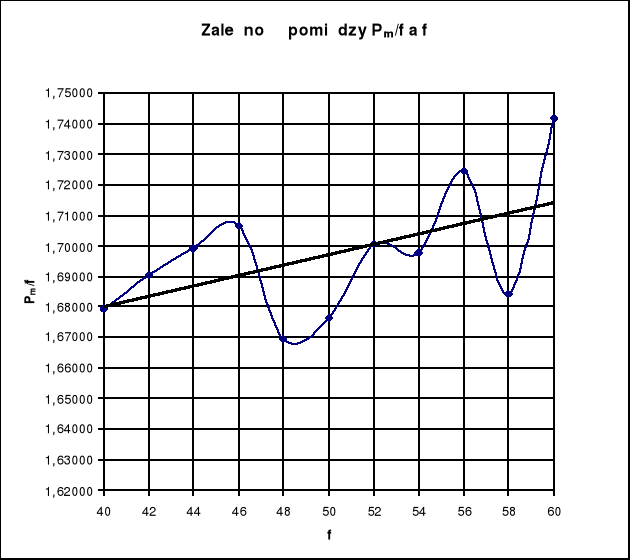
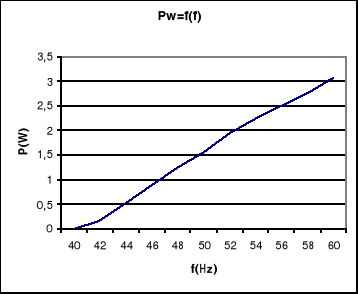
Charakterystyki stratności magnetycznej:
Pomiary dotyczące selsynów:
Pomiary wykonaliśmy mierząc SEM między fazowe przy zmieniającym się kącie od 0 d0 360 stopni co 30 stopni.
Dzieki zmierzonej SEM : E12,E23,E31 i kątowi Obliczyliśmy SEM fazowe E1,E2,E3 i narysowaliśmy charakterystyki:
![]()
;![]()
;![]()
a także:
![]()
![]()
![]()
Stąd wyliczyłem E1 , E2 i E3
![]()
![]()
![]()
Obliczenia wykonaliśmy na podstawie tych wzorów.
Dzieki tym obliczeniom wykonaliśmy charakterystyki:
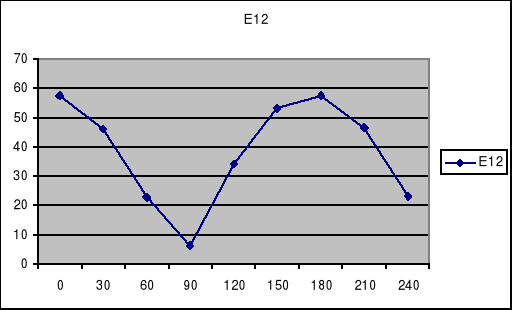
Charakterystyka E12=f()

Charakterystyka E23= f()

Charakterystyka E31= f()
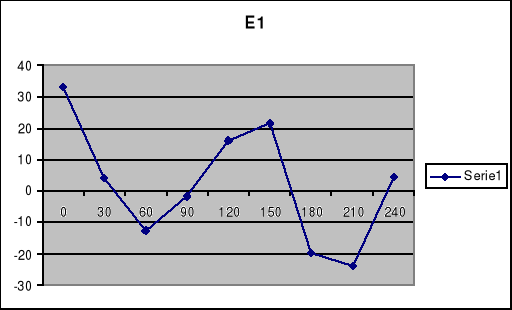
Charakterystyka E1=f(
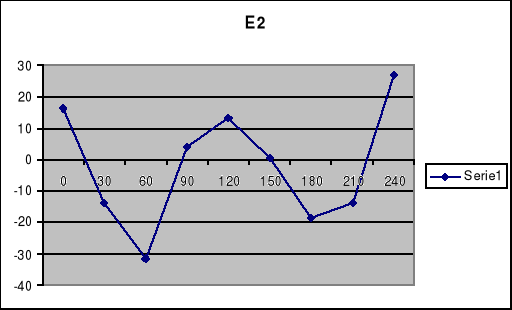
Charakterystyka E2=f()
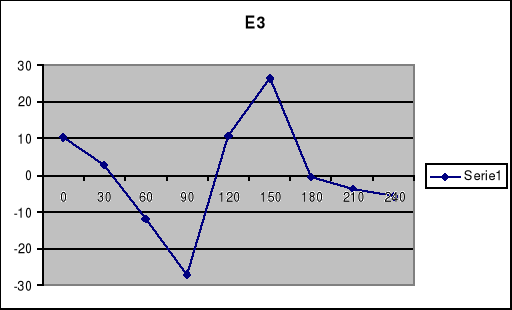
Charakterystyka E3=f()
Kąt niezgodności i jego charakterystyka:
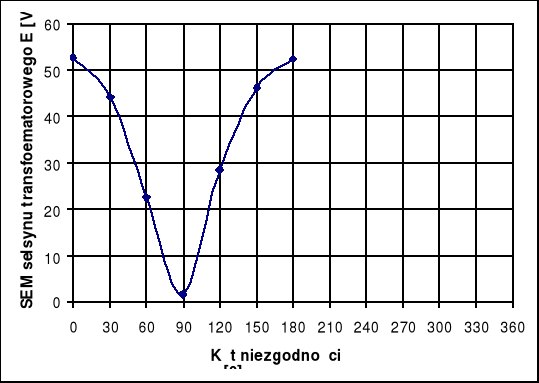
Charakterystyka Ms=f(
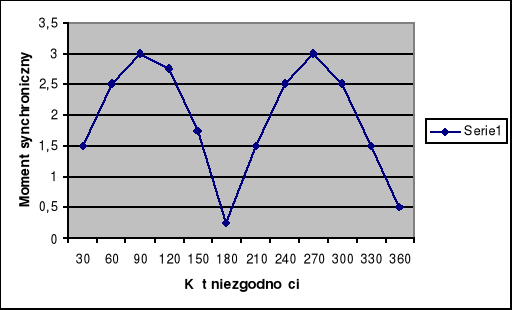
Wnioski:
Zmniejszenie strat od prądów wirowych w rdzeniu obwodu magnetycznego przy zadanej indukcji magnetycznej i częstotliwości można otrzymać, wykonując rdzeń z cienkich blach magnetycznych i izolowanych względem siebie papierem, lakierem lub warstwą ceramiczną lub stosując blachy z materiału ferromagnetycznego o dużej rezystywności. Rezystywność materiału ferromagnetycznego można zwiększyć stosując odpowiednie domieszki stopowe, np. do stali elektrotechnicznej jako domieszkę stosuje się krzem. W środowisku nieruchomym prądy wirowe powstają w skutek zmian strumienia magnetycznego.
Przenikalność magnetyczna ferromagnetyków zmienia się w szerokich granicach. Od niewielkiej wartości początkowej wzrasta wraz ze wzrostem natężenia pola magnetycznego po czym maleje. Na sporządzonym wykresie μw = f(Hm) widoczna jest jedynie malejąca część charakterystyki. Gdyby wykonać obliczenie przy wartościach prądu poniżej 1,5 A zapewne otrzymalibyśmy pełny wykres charakterystyki. Adektywnie odnosi się to do zależności Bm = f (Hm). Obserwujemy natężenie pola magnetycznego przy stosunkowo mniejszym przedziale zmienności indukcji magnetycznej.
Jak wynika z wykresów pętli histerezy dla pierwszych sześciu przypadków pole pętli powiększa się wraz ze wzrostem częstotliwości, która ma znaczący wpływ na straty. Do takiego samego wniosku dojdziemy analizując wykresy od 3 do 6. Jak widać we wszystkich przypadkach poszczególne rosą wraz ze wzrostem częstotliwości.
Wyszukiwarka
Podobne podstrony:
PIII - teoria, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektro
elektra M6a, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektroni
Elektra p3 2, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektron
Nasze sprawko, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektro
Elektra M-1tab, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektr
sprawko trans R, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elekt
elektra P-4, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektroni
sprawko elektra e2, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, El
Elektra p3, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronik
Elektra p3, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronik
M-5, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronika i Ele
PIII - teoria, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektro
elektra P4, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronik
elektra M4, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronik
jasiek pytania, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektr
M2, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronika i Elek
Wnioski do stanu jałowego trafo, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II
Elektra M-2spr, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektr
elektra M5, Studia, SiMR, II ROK, III semestr, Elektrotechnika i Elektronika II, Elektra, Elektronik
więcej podobnych podstron