Laboratorium Wytrzymałości Materiałów |
||
|
Temat: Tensometria statyczna. Naprężenia w zginanej belce. |
|
Data wykonania ćwiczenia:
|
Data oddania sprawozdania:
|
Ocena: |
Szkic belki.
P a
A x
C 100 b
D E
B
l
l = 705 mm
a = 345 mm
b = 5 mm
P = 5,10,15 kN
x - odległość tensometrów od podpory.
Opis stanowiska pomiarowego.
Do przeprowadzonego ćwiczenia zastosowany został układ tensometryczny
mostka Wheatstone`a z aparaturą wzmacniającą. Wykorzystany został również
układ o zwiększonej czułości: rozetę tensometryczną dwuczujnikową.
tablica z wynikami pomiarów i obliczenia.
Lp |
x [mm] |
P [kN] |
XAB |
CAB [mV/V] |
XC |
Cc [mV/V] |
εA·106 |
εB·106 |
γc·106 |
σA [MPa] |
σB [MPa] |
τc |
εc·106 |
1 2 3 |
280 |
5 10 15 |
100 98 61 |
0,1 0,2 0,5 |
40 75 59 |
0,1 0,1 0,2 |
92,5 181,3 282,2 |
-92,5 -181,3 -282,2 |
37 85,2 127,8 |
18,5 36,26 56,44 |
-18,5 -36,26 -56,44 |
11,84 22,19 34,93 |
74 138,7 218,3 |
1` 2` 3` |
100 |
5 10 15 |
44 70 54 |
0,1 0,1 0,2 |
22 50 90 |
0,1 0,1 0,1 |
40,7 64,8 99,9 |
-40,7 -64,8 -99,9 |
0 -55,4 -133,2 |
8,14 12,96 19,98 |
-8,14 -12,96 -19,98 |
6,51 19,8 26,64 |
40,7 92,5 166,5 |
1” 2” 3” |
190 |
5 10 15 |
64 68 42 |
0,1 0,2 0,2 |
22 54 94 |
0,1 0,1 0,1 |
59,2 125,8 77,7 |
-59,2 -125,8 -77,7 |
37 51,8 -192,4 |
11,84 25,16 15,54 |
-11,84 -25,16 -15,54 |
6,51 15,98 27,82 |
40,7 99,9 173,9 |
przykładowe obliczenie εA
gdzie:
XAB - mierzona liczba działek,
A = 100 - kalibracja zakresu,
c - zakres pomiarowy mV/V,
k = 2,15 - stała czujników,
n = 2 - ilość czynnych tensometrów,
p = 1,0056 - wartość stała.
c1=0,1 mV/V
XAB1=100
n=2
k=2,15
A=100
p=1,0056
przykładowe obliczenie γc .
Cc1=0,1 mV/V
Xc1=40
n=1
k=2,15
A=100
p=1,0056
Przykładowe obliczenie σA
σA= E·εA
E=0,2·106 MPa
εA=0,0925·10-3
σA1 = 0,2·0,0925·103=18,5 MPa
Przykładowe obliczenie τc
τc= G ·2εc
G = 80000 MPa - moduł sztywności,
εc= 0,074·10-3
τc = 80000·2·0,074·10-3 = 11,84 MPa
Obliczenie teoretycznych σ i τ
Przykładowe obliczenia:
Mg = RE · x
ΣME = P · a - RD · l = 0
RD = P · a /l
ΣF = RD - RE - P = 0
RE = P - RD
RE = P - P · a / l = P·(1 - a / l)
P = 5kN
x = 280 mm
a = 345 mm
l = 705 mm
Mg = P · (1 - a / l) · x = 714,9 Nm
Wz = 34,2 cm3
T1 = RE = 2557,2 N
Smax = 19,9 cm3
b = 5 mm
I = 171 cm4
Lp. |
Mg [Nm] |
σ [MPa] |
τ [Mpa] |
1 2 3 |
714,9 1429,8 2144,7 |
20,9 41,8 62,71 |
5,95 11,9 17,8 |
1` 2` 3` |
255,3 510,6 765,9 |
7,46 14,9 22,4 |
5,95 11,9 17,8 |
1” 2” 3” |
485,1 970,2 1445,3 |
14,2 28,4 42,6 |
5,95 11,9 17,8 |
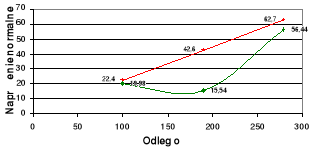
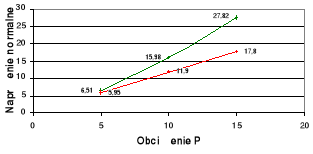
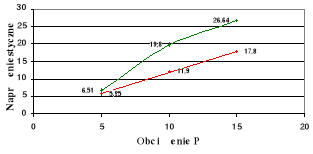
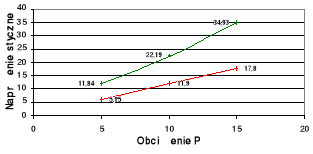
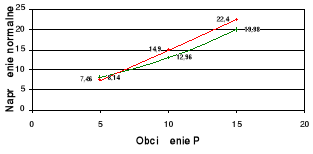
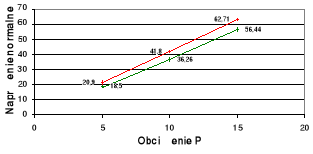
Wykresy zależności σ = σ(P) i τ = τ(P) dla poszczególnych x na tle zbieżności
teoretycznej.
wykresy teoretyczne,
wykresy doświadczalne.
x = 280
x = 100
X = 190
x = 280
x = 100
x = 190
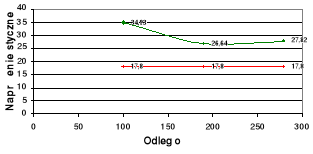
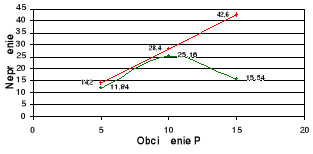
Wykresy rozkładów σ i τ na długości od 0 do a dla P = Pmax na tle rozkładów teoretycznych.
P = 15 kN
Wnioski.
Z porównania wykresów zależności σ = σ(P) i τ = τ(P) dla poszczególnych x na tle zależności teoretycznych i wykresów rozkładów σ i τ na długości od 0 do a dla P = Pmax na tle rozkładów teoretycznych wynika, że wartości wyznaczone doświadczalnie są zbliżone do wartości teoretycznych. Różnice w wartościach naprężeń mogą być spowodowane niedokładnością przyłożonej siły. Siły tej nie dało się dokładnie określić ze względu na bezwładność stosowanej aparatury. Różnice te mogą również wynikać z niedokładności pomiaru odległości usytuowania tensometrów na belce, jak również struktura materiału mogła być niejednorodna, co miało wpływ na wyniki pomiarów. Błąd mógł również wystąpić w samych obliczeniach, gdyż wzory wytrzymałościowe wykorzystywane do obliczeń opierają się na pewnych uproszczeniach.
![]()
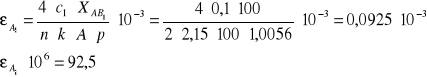
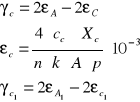
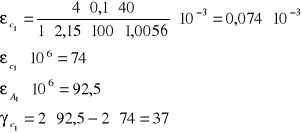
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
wydyma statyczna próba skręcania, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Labv.wytrzymalosc
tensometry1, ZiIP, II Rok ZIP, wytrzymalosc, WYDYMA ROK II semestr III-IV
zadanie zginanie - czesto je daja na kolach!!!, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Wytrzymał
Laboratorium Wytrzymalosci Materialow-cw7, ZiIP, II Rok ZIP, wytrzymalosc, WYDYMA ROK II semestr III
statyka-sc, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Wytrzymałość materiałów
Laboratorium Tensometria-raport moj, ZiIP, II Rok ZIP, wytrzymalosc, WYDYMA ROK II semestr III-IV
LABORA~2, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Wytrzymałość materiałów, Wytrzymałość materiałó
Lab.-Statyczna proba skręcania, ZiIP, II Rok ZIP, wytrzymalosc, WYDYMA ROK II semestr III-IV, WYDYMA
wydyma pomiar twardości metodą Brinella Wickersa i Poldi, ZiIP, II Rok ZIP, Wytrzymałość materiałów,
Statyczna próba rozciągania, ZiIP, II Rok ZIP, wytrzymalosc, WYDYMA ROK II semestr III-IV
Udarność i wyboczenie, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Wytrzymałość materiałów
wydymaaa, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Wytrzymałość materiałów
LABORA~7, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Labv.wytrzymalosc
wytrzymałość ćw.III, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Labv.wytrzymalosc
Brinnel Vickers Poldi, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Wytrzymałość materiałów
LABOR~10, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Labv.wytrzymalosc
wydyma wyznaczanie charakterystyk sprężyn, ZiIP, II Rok ZIP, Wytrzymałość materiałów, Labv.wytrzymal
więcej podobnych podstron