Szymon Kuliński 2009-10-20

LPF Czwartek 7:30 Dr A. Kolarz

Ćw.10 SPRAWDZANIE PRAWA HOOKE'A; WYZNACZANIE MODUŁU YOUNGA

1.Cel ćwiczenia

Dla danej stalowej liny sprawdzenie prawa Hooke'a, oraz wyznaczenie modułu Younga.

2.Wstęp teoretyczny

Ciało pod wpływem siły odkształca się. Siła zewnętrzna odkształcająca ciało wykonuje pracę przeciwko siłom wewnętrznym. Skutkiem działania sił jest przyrost długości (Δl). Prawo Hooke'a mówi, że „Jeżeli występujące w ciele naprężenia są dostatecznie małe, to wywołane przez nie odkształcenia względne są do nich wprost proporcjonalne”. Konsekwencją tego jest fakt, iż gdy zaczniemy zwiększać obciążenie a co za tym idzie siłę rozciągającą od pewnego obciążenia Δl zacznie zmieniać się nie proporcjonalnie do siły.

Doświadczenie:

Sprawdzanie prawa Hooke' a w doświadczeniu polega na wykonaniu kilku pomiarów wydłużenia stalowego drutu pod wpływem znanego obciążenia Q = mg i sporządzeniu wykresu. Wzór na obliczenie modułu Younga przedstawia się następująco:

1. Konstrukcja mocująca

2. Badany drut

3. Wskaźnik A

4. Uchwyt mocujący drut

5. Mikroskop pomiarowy M

6. Obciążenie stałe (szalka)

7. Walce metalowe

3. Wyniki pomiarów

Tab1.Wartość pomiaru dla różnych obciążeń[dz]

Próba\ Masa	0 Ciężarków	1 Ciężarek	2 Ciężarki	3 Ciężarki	4 Ciężarki	5 Ciężarki
1	3,5	3,29	2,98	2,67	2,33	2,11
2	3,6	3,29	2,99	2,61	2,35	2,11
3	3,51	3,3	2,96	2,64	2,35	2,06
4	3,48	3,29	2,99	2,69	2,32	2,10
5	3,58	3,28	2,93	2,64	2,33	2,09
Średnia	3,53	3,29	2,97	2,65	2,34	2,09
Odchylenie standardowe	0,11	0,01	0,05	0,06	0,02	0,04

Tab2.Pomiar szerokości wskaźnika pod mikroskopem

Próba	Szerokość[dz]
1	0,44
2	0,43
3	0,47
4	0,51
5	0,5

Tab3.Pomiar wskaźnika śruba mikrometryczną

Próba	Szerokość[mm]
1	2,10
2	2,00
3	1,91
4	1,97
5	1,97

Skoro 0,47 mm = 1,99dz

To 1mm = 4,23dz

Więc 1dz = 0,23mm

Tab4.Odległość w mm od punktu rozpoczęcia pomiarów (l).

Próba\ Masa	0 Ciężarków	1 Ciężarek	2 Ciężarki	3 Ciężarki	4 Ciężarki	5 Ciężarki
1	0,17	0,22	0,30	0,37	0,45	0,50
2	0,15	0,22	0,29	0,38	0,44	0,50
3	0,17	0,22	0,30	0,38	0,44	0,51
4	0,18	0,22	0,29	0,36	0,45	0,50
5	0,15	0,23	0,31	0,38	0,45	0,51
Średnia	0,17	0,22	0,30	0,37	0,45	0,51

Tab6.Grubość drutu [mm]

0,83
0,82
0,83
0,84
0,82
0,80
0,81
0,83
0,82
0,80

Tab7.Wagi odważników[g]

998,7

998,4

998,5

998,9

998,3

998,5

Średnia waga wynosi 998,5[g] ± 0,1

Średnia grubość drutu wynosi

0,82 mm= 0,082 cm = 0,00082m ± 0,00001

Długości l wynosi 60,1cm = 601mm=0,601m ± 0,001

4.Obliczenia

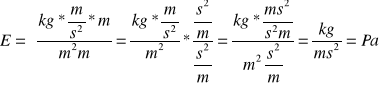
Dla uśrednionych danych otrzymujemy:

Należy teraz obliczyć błąd względny, stosując do wykorzystywanego wyżej wzoru metodę różniczki logarytmicznej.

Obliczymy teraz błąd bezwzględny otrzymanej wartości E:

5.Wyniki i Wnioski

E=159,2 +/- 0,2[GPa]

W przeprowadzonym doświadczeniu zaistniały okoliczności, które umożliwiły powstanie wielu błędów. Z pewnością największe znaczenie możemy przypisać błędom powstałym z powodu niedoskonałości przyrządu pomiarowego, jakim jest mikroskop, a spowodowane tym, iż nie można uzyskać ostrości wystarczającej do odczytu poprawnego wyniku pomiaru. Aby zminimalizować wpływ błędów na dokładność wyznaczenia modułu Young'a w tym ćwiczeniu należy zadbać o zapewnienie większej stabilności układu pomiarowego oraz o takie umocowanie drutu, aby uniemożliwić jego skręcanie podczas zwiększania obciążenia. Jednakże pomimo tych błędów otrzymana wartość modułu Young'a jest zadawalająca i w dużej mierze jest porównywalna z jego wartością odczytaną z tablicy stałych fizycznych. Jednak przy pomiarach ma miejsce stosunkowo duży błąd względny wynikający z prostoty przyjętej w doświadczeniu metody. Przykładem przyjętych uproszczeń może być nie branie pod uwagę błędu wynikającego ze zmieniającej się w trakcie doświadczenia średnicy drutu.

---