Szymon Kuliński 2009-10-20

LPF Czwartek 7:30 Dr A. Kolarz

Ćw.20 Wyznaczanie współczynnika załamania światła

za pomocą reflektometru oraz mikroskopu

1.Cel ćwiczenia

Wyznaczenie współczynnika załamania światła dla podanych cieczy i ciał stałych za pomocą reflektometru Abbego oraz mikroskopu.

2. Wstęp teoretyczny

Współczynnik załamania ośrodka jest miarą zmiany prędkości rozchodzenia się fali w danym ośrodku w stosunku do prędkości w innym ośrodku.Dokładniej jest on równy stosunkowi prędkości fazowej fali w ośrodku odniesienia do prędkości fazowej fali w danym ośrodku. Fala elektromagnetyczna, przechodząc przez granicę dwóch ośrodków ulega częściowemu załamaniu i odbiciu, czego wartość określa właśnie współczynnik załamania n = f(λ). Wartość bezwzględna tego współczynnika wynosi:

Kierunki rozchodzenia się fali odbitej i załamanej opisują prawa Snelliusa:

Jeżeli współczynnik załamania światła jest większy w jednym ośrodku niż w drugim, to w miarę wzrostu kąta padania rośnie także kąt załamania i przy tzw. kącie granicznym (
) osiąga on wartość
°; wszystkie promienie padające na powierzchnię pod kątem większym niż
zostają od tej powierzchni całkowicie odbite

Na tej zasadzie działa reflektometr Abbego.

Pomiar reflektometrem Abbego polega na obserwacji promieni przechodzących przez układ dwóch pryzmatów. Uzyskany w ten sposób kąt graniczny pozwala na wyliczenie współczynnika załamania światła z prawa Snelliusa.

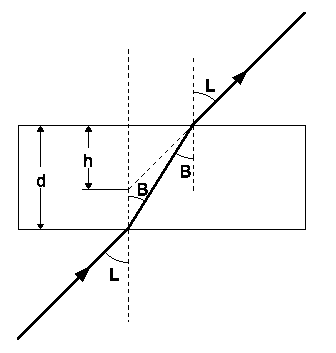
Drugim sposobem na pomiar współczynnika załamania światła jest pomiar grubości rzeczywistej i pozornej za pomocą mikroskopu.

Współczynnik załamania światła jest równy:

Co dla mały kątów może być równe ilorazowi sinusów. I tym samym wyrażać się wzorem:

3.Badanie współczynnika załamania dla szkła i roztworu sacharozy za pomocą mikroskopu.

Błędy pomiaru dla odległości będzie obliczany metodą różniczki zupełnej. Dla pomiarów za błąd jednostkowego pomiaru przyjmujemy dokładność mikroskopu (0,01 mm).Błąd pomiaru n będzie wyznaczany wzorem:

Δn =

Tab1. Wyniki pomiaru za pomocą mikroskopu

Substancja	I [mm]	II [mm]	III [mm]	d=III - I	∆d	h=III - II	∆h	n	∆n
Szkoło	6,20	6,82	8,03	1,82	0,02	1,2	0,02	1,517	0,042
Sacharoza(15%)	6,55	7,05	8,78	2,23	0,02	1,73	0,02	1,289	0,015

4. Badanie współczynnika załamania światła dla zestawu cieczy oraz wody i roztworu sacharozy za pomocą reflektometru Abbego

Tab2.Wyniki pomiarów za pomocą reflektometru Abbego

Ciecz	n	∆n
Woda destylowana	1,336	0,001
Sacharoza(15%)	1,365
X	1,472
20%	1,383
40%	1,422
80%	1,511
100%	1,551

5. Wyniki i wnioski

Wyniki pomiaru mikroskopowego dla szkła wynoszący 1,517±0,04 mieszczącego się w mierze odczytanej z tablic, dla szkła wynoszącej 1,56-1,60. Wynik mimo małego błędu względnego jest bardzo niedokładny. Niedokładność ta wynika z nieuwzględnienia głębokości rysy jak i subiektywnej oceny ostrości mikroskop, a w przypadku cieczy z faktu, iż pył nie tworzył jednorodnej powierzchni i częściowo tonął. Jak pokazało doświadczenie z roztworem sacharozy wyniki pomiaru mikroskopowego i pomiaru wykonanego przy pomocy reflektometru Abbego różnią się od siebie dosyć znacznie( 0,07). W pomiarach za pomocą reflektometru nie uwzględniliśmy również błędu wynikającego z faktu, iż na pryzmatach mimo starannego oczyszczenia mogła zostać część poprzedniego roztworu. Z załączonego wykresu wynika, że ciecz X ma stężenie około 65%.

---