1.2 BELKA STROPOWA.

1.2.1 ZESTAWIENIE OBCIAŻEŃ NA 1m² PŁYTY STROPOWEJ.

Obciążenia stałe:

Lp.	Obciążenia stałe	wartości charakterystyczne	współczynnik obciążenia	wartość obliczeniowa
1.	płyta żelbet. monolityczna gr.3.0 cm wylewana na podkładzie z blachy fałdowej	0.03m. x 25kN/m^3 +0.11kN/m^2=0.86kN/m^2	1.1	0.946kN/m^2
2.	płyta pilśniowa porowata o gr.12.5mm chroniona papą smołową powlekaną,na podkładzie gr.30mm	0.62kN/m^2	1.3	0.806kN/m^2
3.	Gładż cem. o gr.35mm	0.735kN/m^2	1.3	0.956kN/m^2
4.	Płytki PCV gr. 3 mm	0,070kN/m^2	1.3	0,084kN/m^2

RAZEM: g_k=2,285kN/m² g_d=2,792kN/m²

obciążenia zmienne:

Lp.	obciążenia zmienne	wartości charakterystyczne	współczynnik obciążenia	Wartości obliczeniowe
1.	Ścianki działowe	1,25kN/m^2	1,2	1,5kN/m^2
2.	obciążenia użytkowe	2.0 kN/m^2	1.4	2.8kN/m^2

RAZEM; p_k= 3,25kN/m² p_d=4,3kN/m²

Obciążenia całkowite; q_d=g_d+p_d=7,092kN/m²

1.2.2 WSTĘPNE PRZYJĘCIE PRZEKROJU BELKI STROPOWEJ.

Wstępnie przyjęto belkę o przekroju z PE 220 i masie 26,2kg/m.=0.262kN/m.

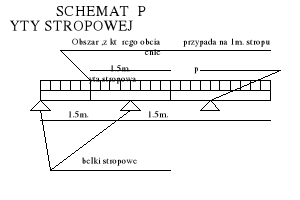
Wielkość obciążeń przypadające na 1m. Długości belki stropowej z uwzględnieniem ciężaru własnego belki stropowej ;

q_db=7,092kn/m² x 1.5m. + 0.262kN/m. x 1.1 = 10,926kN/m².

Potrzebny wskaźnik wytrzymałości przekroju poprzecznego belki stropowej:

σ W <f_d W=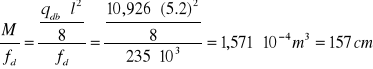
³

gdzie;

l-obliczeniowa rozpiętość belki

Przyjęto dwuteownik 220 PE o Wx = 252 cm³ i o ciężarze 0,262 kN/m

1.2.3 ZESTAWIENIE OBCIĄŻEŃ NA 1m. DŁUGOŚCI BELKI STROPOWEJ.

Obciążenia stałe	Wartości charakterystyczne	Współczynnik obciążenia	Wartości obliczeniowe
Obciążenie płytą	2,285kN/m^2 x 1.5m.=3,427kN/m^2		2,792kN/m^2 x 1.5 = 4,188kN/m^2
Ciężar własny żebra	0.262kN/m^2	1.1	0.288kN/m^2

RAZEM: g_k=3,889kN/m g_d=4,476kN/m

Obciążenia stałe	Wartości charakterystyczne	Współczynnik obciążenia			wartości obliczeniowe
Ścianki działowe	1,25x1,5=1,875kN/m			1,5x1,5=2,25kN/m
Obciążenia użytkowe	2.0kN/m. X1.5m.=3,0kN/m			2.8kN/m. x1.5m.=4,20kN/m

RAZEM : p_k=4,875kN/m p_d=6,45kN/m.

1.2.4 PRZYJĘCIE KOMBINACJI POODSTAWOWEJ OBCIĄŻEŃ W STANIE GRANICZNYM NOŚNOŚCI.

γ_fiG_ki + _ γ_ki Q_ki

Podstawiając wartości liczbowe otrzymamy:

Q_d=4,476kN/m.+1.0 x 6,45+ 0,9 x 1,625=12,388kN/m.

1.2.5 PRZYJĘCIE KOMBINACJI PODSTAWOWEJ OBCIAŻEŃ W STANIE GRANICZNYM UŻYTKOWANIA.

G_ki+Q_k

Podstawiając wartości liczbowe otrzymamy:

Q_k=3,685kN/m. + 4,875kN/m.=8,564kN/m

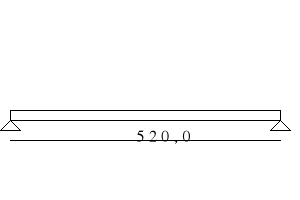
 SCHEMAT OBLICZENIOWY BELKI STROPOWEJ.

Belka stropowa stanowi zespół pięciu belek swobodnie podpartych o teoretycznej rozpiętości przęseł l_t=5.2m.Rozpietosć obliczeniowa przęseł skrajnych :l₀=(1+0.025)l_t=1.025 x 5.2m.=5.330m.,

przęseł środkowych l₀=l_t=5.2m.

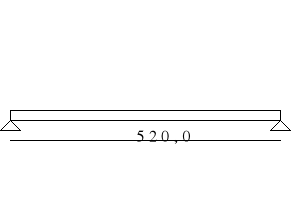
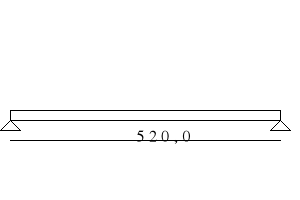
1.1.2.7 OBLICZENIE WARTOSCI SIŁ WEWNĘTRZNYCH W BELCE STROPOWEJ

Obciążenie obliczeniowe na 1m. długości belki:Q_d=12,388kN/m.

Maksymalny moment zginający :

Maksymalna siła poprzeczna:

1.2.8. WYMIAROWANIE BELKI STROPOWEJ .

Sprawdzenie nośności belki stropowej:

Dane dotyczące I 180:

H=180mm;b_f=82mm;t_w=6.9mm;t_f=10.4mm;r=6.9mm;A=27.9cm²;I_x=1450cm⁴;I_y=81.3cm⁴;W_x=161cm³;W_y=19.8cm³; i_x=7,2cm;i_y=1.71cm .

a) sprawdzenie klasy przekroju

  f_d=305MPa-dla stali 18G2

Sprawdzenie klasy przekroju dla ścianki środnika;

h_w (H- 2r-2t_f) (180-2 x6.9 -2 x 10.4)

= = = 21.07 < 66=54.12 (ścianka środnika spełnia warunki

t_w t_w 6.9 klasy 1)

Sprawdzenie klasy przekroju dla ścianki pasa;

b_f 0.5(b_f-2r-t_w) 0.5(82-2 x 6.9 -6.9)

= = =2.947<9 (ścianka pasa jest klasy 1)

t_f t_f 10.4

Przekrój belki stopowej zaliczono do przekrojów klasy 1,a więc może on osiągnąć nośność przegubu plastycznego.

b) Ustalenie nośności obliczeniowej przekroju belki stropowej przy jednokierunkowym zginaniu;

-nośność obliczeniowa przy zginaniu ,

M_R=_p W f_d _p.-obliczeniowy wsp. Rezerwy plastycznej przekroju _p =1.07 dla I180

W_x=161cm³-wskaźnik wytrzymałości przekroju belki,

f_d=305MPa-wytrzymałość stali.

M_R=1.07 x 161 x 305 x 10³ = 52.54kNm

c) Sprawdzenie czy należy uwzględnić wpływ zwichrzenia;

Według normy elementy ,w których pas ściskany jest stężony sztywną tarczą są konstrukcyjnie zabezpieczone przed zwichrzeniem (utratą płaskiej postaci zginania).Za sztywną tarczę można uznać żelbetową płytę stropową.

d) Określenie nośności przekroju podporowego belki ,w którym występuje siła poprzeczna V_d=21.82kN

sprawdzenie:

h_w 145.4

= = 21.07< 70

t_w 6.9

Ponieważ warunek smukłości jest spełniony ,nośność obliczeniowa ma wartość;

V_R=0.58A_V f_d =0.58 x 900 x 305 =159210=159.21 kN

gdzie:

A_V-pole przekroju czynnego przy ścinaniu

_V=h_w x t_w=180 x 5.0 = 900mm²

e) Ustalenie współ.zwichrzenia -dla elementów zabezpieczonych przed zwichrzeniem _L=1.0

f) Sprawdzenie nośności elementu

W przypadku elementu zginanego;

M. M.=27.96kNm-max moment zginający

< 1 _L=1.0-współ.zwichrzenia

_L M_R M_R=52.54kNm-ność obliczeniowa przy zginaniu

Podstawiając otrzymujemy;

27.96

=0.53<1.0

1.0 x 52.54

W przekroju podporowym należy ponadto sprawdzić warunek;

V=21.82kN<V_R=159.21kN

1.2.9SPRAWDZENIE WARUNKU SZTYWNOŚCI

Wartość obciążenia charakterystycznego przypadającego na 1m. długości belki wynosi;

Q_k=6.506kN/m. Dopuszczalna wielkość ugięcia dla belek stropowych wynosi l/250.

Określenie wielkości ugięcia (E=205GPa = 205000 MPa ; I_x=1450cm⁴):

-przęsło skrajne:

5 x 6.567 x (5125)⁴ 5125

a= = 19.84mm ~ a_gr= = 20.5mm,(3%)

384 x 205000 x1450 x 10⁴ 250

-przęsło środkowe

5 x 6.567 x (5000)⁴ 5000

a= = 17.98mm < a_gr= = 20mm,(10%)

384 x 205000 x 1450 x 10⁴ 250

 SPRAWDZENIE OPARCIA ŻEBRA NA MURZE.

Przy oparciu belki na murze należy sprawdzić nacisk jaki wywiera belka stropowa na mur wg pkt. 5.4 normy murowej.

V<m_d x R_m x F_d,

gdzie:

V-siła działająca na powierzchnię docisku F_d równa reakcji podporowej belki stropowej ; V=21.82kN

m_d-współczynnik korekcyjny określony wzorem ;

m_d= _d -(δ_mr/R_m)( _d-1),

gdzie:

R_m-wytrzymałość obliczeniowa muru niezbrojnego na ściskanie;

R_m=R_mk/γ_m.

Gdzie;

R_mk=wytrzymałość charakterystyczna muru na ściskanie : dla muru z cegły ceramicznej pełnej przy wytrzymałości średniej cegieł 15MPa i marce zaprawy 10-R_mk=3.3MPa,

γ_m.-współczynnik materiałowy: γ_m.=1.3,

Po podstawieniu otrzymamy;

R_m=R_mk/γ_m.= 3.3/1.3=2.54MPa

Maksymalna długość oparcia wynosi;

b=150+H/30[mm] = 150+180/30=156[mm]

gdzie;

H-wysokość belki stropowej ; H=180mm

Szerokość oparcia belki na murze wynosi : a=b_f=82 mm , a szerokość muru :h=380 mm

Określenie wartości współczynnika rozdziału obciążenia _d;

F_r=b(2b+a)=156(2 x 156 +82)=61464mm²

F_d=ab=82 x 156=12792 mm²

Sprawdzenie warunków konstrukcyjnych:

a 82

= = 0.216<1 _max=2.0,

h 380

_d=1.68< _max=2.0,

Średnie naprężenia dociskowe na powierzchni rozdziału -σ_mr

N 21.82 x 10³

σ_mr= = =0.355MPa

F_r 61464

Wyznaczenie wartości współczynnika m_d;

m_d =

Sprawdzenie nośności muru;

N=21820N < 1.591 x 2.54 x 12792 =51694N

1.2.11. PROJEKTOWANIE BELEK STROPOWYCH PRZY UWZGLĘDNIENIU PODATNOSCI POŁĄCZEŃ BELEK Z BLACHOWNICAMI.

Określenie przekroju belki stropowej przy uwzględnieniu połączeń podatnych

Połączenie belki stropowej z podciągiem ukształtowano na jednokrotną przykładkę na środniku belki stropowej .Wartość obliczeniowa obciążenia Q_d=8.5161kN/m ,wartość charakterystyczna Q_k=6.567kN/m.

Określenie sztywności połączenia

Postać ogólna równania charakterystyki M.- dla węzła na jednokrotną przykładkę na środniku belki stropowej :

=4.28(KM) x 10^-3 + 1.45(KM) x 10^-9 + 1.51(KM) x 10^-16

Określenie wartości stałej standaryzacji K;

K=d^-2.4x t^-1.81x g^0.15=0.1367

gdzie ;

d- wysokość przykładki w calach [in];d=140mm=5.51(1inch=2.54cm),

t-grubość przykładki w calach t=9mm=0.354in,

g-odległość od osi skrajnego rzędu śrub do osi środnika podciągu w calach

g=30+20+10+0.5 x9=64.5mm=2.54in

Postać szczegółowa równania charakterystyki M.- dla węzła na jednokrotną przykładkę na środniku belki stropowej ;

=4.28(0.1367x M.)x 10^-3+1.45(0.1367x M.)x10^-9+ 1.51(0.1367xM)x 10^-16

gdzie ;

M.-moment zginający w węźle w [in-kip];1in-kip = 0.113 kNm.

Ustalenie sztywności połączenia podatnego;

1 M_i

K_r=  , dla i=3-5

2 _i

gdzie;

i-liczba punktów na części prostoliniowej charakterystyki M.- węzła przyjęta do wyznaczenia

średniej wartości sztywności początkowej .

Lp.	Moment[M.]	Moment[M.]	Obrót całkowity[]		Sztywność [M/]
	[kNm]	[in-kip]	[rad]		[in-kip/rad]
1. 2. 3. 4. 5.	0.5 1 2 5 7	4.42 8,85 17,7 44,25 61,95	0.0025860 0.0051778 0.0103557 0.0258893 0.0362450		1709,2 1709.2 1709.2 1709.2 1709.2
M/=		8545,89
Kr(1-5)=		854.6

Sztywność połączenia ;K_r=854,6 in-kip/rad=96.57kNm/rad.

Ustalenie sztywności bezwymiarowej połączenia;

K_r x I 96.57x 10⁶Nmm/rad x 5000mm 1

K_r= = =0.1624

E x I_x 205000N/mm² x 1450 x 10⁴mm⁴ rad

gdzie;

K_r-sztywność połączenia ;K_r=96.57kNm/rad.

I-rozpiętość obliczeniowa belki stropowej ;l=5.0 m,

E=205GPa=205000MPa,

I_x-moment bezwładności przekroju I_x=1450cm⁴

Określenie wartości momentów zginających w belce stropowej przy uwzględnieniu ograniczenia swobody obrotu końca belki stropowej w połączeniu z podciągiem ;

-moment zginający w środku rozpiętości belki stropowej ;

K_r+6 g₀x l² 0.1624 +6 8.5161 x (5.0)²

M_B= x = x =0.95x26.61 =25.28kNm

3(K_r+2) 8 3(0.1624 +2) 8

- moment zginający na podporze podatnej;

2 x K_r g₀x l² 0.1624 x 2 8.5161 x (5.0)²

M_s= x = x =0.05x26.61 =1.331kNm

3(K_r+2) 8 3(0.1624 +2) 8

Redukcja momentu zginającego w środku rozpiętości przęsła belki stropowej w stosunku do wartości obliczonej przy założeniu , że belka połączona jest z podciągiem w sposób przegubowy wynosi (1-0.95) x 100%=5%

Określenie wartości ugięcia w belce przy uwzględnieniu ograniczonej swobody obrotu końca belki w połączeniu z podciągiem;

K_r+10 5 g_nxl⁴ 0.1624 +10 5 6,567x(5000)⁴

a_b= x x = x x =0.94 x 17.98=16.899mm

5 xK_r +10 384 ExI_x (5x0.1624+10) 384 205000x1450 x 10⁴

Redukcja ugięcia w środku rozpiętości przęsła belki stropowej w stosunku do wartości obliczonej przy założeniu , że belka połączona jest z podciągiem w sposób przegubowy wynosi (1-0.94) x 100%=6%

Określenie potrzebnego przekroju belki przy uwzględnieniu ograniczenia swobody obrotu końca belki W_pod;

M_B 25.28x10⁶

w_pod= = = 82885.25mm³=82.88cm³<W_prz=161cm³

f_d 305

gdzie ;

W_pz-przyjęto uprzednio wskaźnik wytrzymałości belki stropowej przy traktowaniu połączenia belki stropowej z podciągiem jako przegubowe (swoboda obrotu końca belki stropowej na p. odporze). 6 M10 - 6.8

40 I 180

20

30

30

20

40

9 20 30 20

10

PROJEKT KONSTRUKCJI NOŚNEJ STROPU:Belka stropowa.

3

---