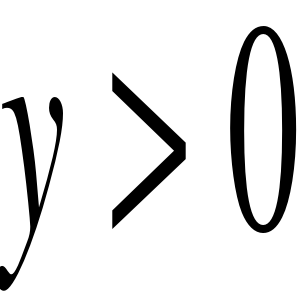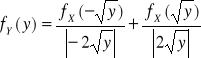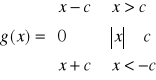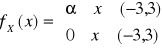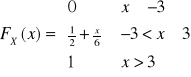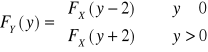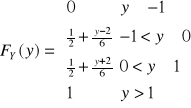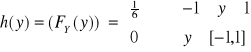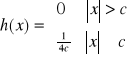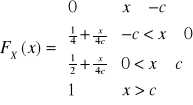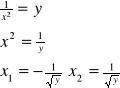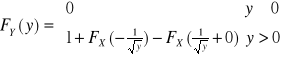FUNKCJE ZMIENNYCH LOSOWYCH - c.d.

Tw: X - ma rozkład ciągły

jest ciągła i nie jest stała na żadnym przedziale

równanie
ma co najwyżej przeliczalną ilość rozwiązań

Jeżeli
są to wszystkie rozwiązania równania
takie, że
, to

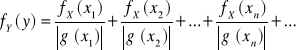
dla
takich, że równanie
posiada rozwiązania spełniające
oraz
w pozostałych przypadkach.

Np.:

(

)

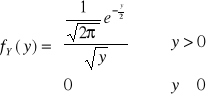
Tw:

dow:

Wniosek:

Zał:
przedział lub suma przeliczalnej ilości przedziałów

np2.:

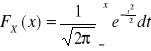
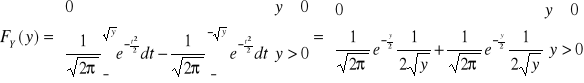
np3.:

I. znaleźć związek między dystrybuantami
i

1. 
   
   

2. 
   
   

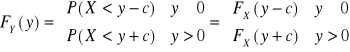
Jeżeli zmienna losowa X jest typu ciągłego, a
jest w pewnym przedziale stała, ale nie schodkowa, to zmienna losowa
jest typu mieszanego.

Np4.: X ma rozkład jednostajny na przedziale
, a
z poprzedniego dla

Jednostajny ⇔

(aby pole było 1)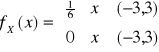

II. Znaleźć efektywny wzór dla

III. Znaleźć rozkład zmiennej losowej Y

(wyliczone wcześniej)

Np5.:

[
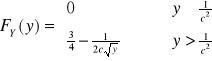
nie jest dystrybuantą - gdzie błąd? ]

3

Luke Rachunek prawdopodobieństwa-wykład 7.5.2k+1

---