Tadeusz Malinowski nr. indeksu 30081

Ewa Malinowska nr. indeksu 30080

grupa 206

Praca semestralna z matematyki- sem.II.

Macierze w ekonomii

1. Pojęcie macierzy

2. Przepływy międzygałęziowe

3. Model Leontiewa

4. Przykłady

I. OKREŚLENIE MACIERZY I JEJ TYPY

Macierzą o wymiarze m x n nazywamy prostokątną tablicę liczb rzeczywistych posiadającą m - linii poziomych zwanych wierszami i n - linii pionowych zwanych kolumnami. Liczby występujące w tablicy (macierzy) nazywamy elementami tej macierzy. Macierze oznaczamy dużymi literami A, B, C... W ogólnej postaci macierz możemy zapisać na dwa sposoby:

Parę liczb m x n nazywamy wymiarem macierzy. W szczególności, jeżeli m = n to macierz nazywamy macierzą kwadratową i możemy wówczas powiedzieć, że macierz ta jest stopnia n. Zapisujemy to w sposób:

A
.

Przekątna główna macierzy kwadratowej A stopnia n jest to ciąg: (a₁₁, a₂₂, …., a_nn) wyrazów tej macierzy o równych indeksach.

Dwie macierze nazywamy podobnymi jeżeli mają ten sam wymiar.

Macierz posiadającą tylko jedną kolumnę nazywamy macierzą jednokolumnową, a macierz posiadającą jeden wiersz nazywamy macierzą jednowierszową - macierze takie nazywamy również wektorami.

Rodzaje macierzy kwadratowej:

- macierz jednostkowa -

1.1 Działania na macierzach

1.1.1 Równość macierzy

Dwie macierze są równe, jeżeli mają ten sam wymiar (są podobne) i mają odpowiednie elementy równe.

Dwie macierze A i B są równe wtedy i tylko wtedy gdy m=m', n=n' oraz aij=bij.

1.1.2 Dodawanie macierzy

Dodawać można tylko macierze podobne. Sumą z macierzy podobnych jest macierz tego samego wymiaru, w której elementy są sumami odpowiednich elementów tych macierzy.

Sumą macierzy A i B nazywamy macierz C = c_ij=a_ij+b_ij. Dodajemy tylko macierze o tych samych wymiarach.

Przykład:

Jeżeli

Własności dodawania macierzy:

1. Dodawanie macierzy jest przemienne:< B>A+B=B+A

2. Dodawanie macierzy jest łączne: (A)+(B)+C=A+(B+C)

3. Macierz zerowa jest elementem neutralnym dodawania macierzy: A+O=O+A=A

4. Dla dowolnej macierzy A istnieje macierz A' taka, że A+A'=O

Macierz A' spełniającą warunek A+A'=O nazywamy macierzą przeciwną macierzy A i oznaczamy -A.

1.1.3 Mnożenie macierzy przez liczbę

Iloczynem macierzy A przez liczbę D nazywamy macierz B = DA = Da_ij

Dowolną macierz mnożymy przez liczbę w ten sposób, że każdy jej element mnożymy przez tę liczbę.

Przykład:

Jeżeli

Własności mnożenia macierzy:

1.1.4 Mnożenie dwóch macierzy

Iloczynem
nazywamy macierz
której elementy wyznaczone są ze wzorów:

Do mnożenia macierzy często stosuje się tzw. schemat Falka. Mnożenie macierzy nie jest przemienne
. Może się zdarzyć, że jeden z tych iloczynów istnieje, a drugi nie. Nawet jeżeli oba te iloczyny istnieją to nie muszą być równe.

1.2 Wyznaczniki

Wyznacznikiem nazywamy liczbę przypisaną każdej macierzy kwadratowej, inaczej mówiąc każdej macierzy kwadratowej można przypisać liczbę, którą nazywamy wyznacznikiem. Wyznacznik można zdefiniować w zależności od stopnia macierzy:

1. n=1

2. n=2

(różnica iloczynów wyrazów przekątnej głównej i przekątnej bocznej)

3) n>=3

Każdemu elementowi dowolnej macierzy kwadratowej można przypisać liczbę zwaną dopełnieniem algebraicznym tego elementu

Weźmy element
tej macierzy. Dopełnienie algebraiczne tego elementu oznaczmy przez
. Wyraża się ono następującym wzorem:

- jest to wzór na dopełnienie algebraiczne

jest wyznacznikiem macierzy powstałej z danej macierzy przez skreślenie i-tego wiersza i j-tej kolumny macierzy . Tak otrzymana macierz jest stopnia n-1, dlatego wyznacznik nazywamy podwyznacznikiem lub minorem.

Niech będzie dana macierz A

Wyznacznikiem dowolnej macierzy kwadratowej nazywamy liczbę równą sumie iloczynów elementów pierwszego wiersza pomnożonych przez ich dopełnienie algebraiczne.

Własności wyznaczników

1. Wyznacznik nie zmieni wartości, jeżeli zamienimy w nim wiersze na kolumny.

2. Jeżeli w wyznaczniku zamienimy ze sobą dwa wiersze lub dwie kolumny to wyznacznik zmieni jedynie znak.

3. Jeżeli w wyznaczniku występuje kolumna lub wiersz samych zer to taki wyznacznik równy jest zeru.

4. Jeżeli wyznacznik posiada dwa wiersze lub dwie kolumny identyczne to jest równy zeru.

5. Jeżeli w pewnym wierszu lub kolumnie wyznacznika występuje czynnik wspólny to czynnik ten można wyłączyć przed wyznacznik. Własnośc ta oznacza, że aby pomnożyć wyznacznik przez liczbę należy przez tę liczbę pomnożyć jeden jego wiersz lub kolumnę.

6. Wyznacznik jest równy zeru, jeżeli posiada dwa wiersze lub dwie kolumny proporcjonalne.

7. Wyznacznik nie zmieni wartości jeżeli do pewnego wiersza lub kolumny dodamy inny wiersz lub kolumnę pomnożone przez dowolną liczbę.

8. Wyznacznik równy jest sumie iloczynów elementów dowolnego wiersza lub kolumny pomnożony przez dopełnienia algebraiczne.

Najszybszą metodą obliczania dużych wyznaczników (co do wymiaru) jest metoda Gauss'a. Polega ona na tym, że sprowadzamy ten wyznacznik do postaci trójkątnej (pod główną przekątną występują same zera). Wyznacznik postaci trójkątnej równy jest iloczynowi elementów występujących na głównej przekątnej.

Zastosowanie macierzy w ekonomii można przedstawić na przykładzie tzw. przepływów międzygałęziowych , czyli produktów wytworzonych w jednej gałęzi, a zużytych przez inną gałąź przemysłu rozpatrywanej gospodarki.

II. PRZEPŁYWY MIĘDZYGAŁĘZIOWE

Analiza przepływów międzygałęziowych dotyczy funkcjonowania złożonych układów gospodarczych. Twórcą tej powszechnie znanej i stosowanej na świecie metody analizy ekonomicznej jest amerykański uczony, laureat nagrody Nobla w dziedzinie ekonomii w 1973 r., Wassily Leontief.

Tablica przepływów międzygałęziowych (TPM) zawiera statystyczny opis działalności produkcyjnej poszczególnych gałęzi rozpatrywanego układu w ustalonym okresie (zwykle w ciągu roku). Wszystkie wielkości występujące w TPM są wyrażone w ujęciu wartościowym. Zastosowaną jednostkę pieniężną, na przykład 1zł, 1 mln zł, 1 mln $, oznaczamy w skrócie j.p. Każdej gałęzi odpowiada jeden wiersz i jedna kolumna TPM. Tablica 1 jest tablicą przepływów międzygałęziowych n-gałęziowego zamkniętego układu gospodarczego (nie uwzględnia się wymiany gospodarczej z zagranicą), a występują w niej następujące elementy, ,i,j=1,2,...,n:

X_i - wartość produktu globalnego i-tej gałęzi,
x_ij - wartość produktu wytworzonego w gałęzi i-tej, a zużytego w gałęzi j-tej, zwana przepływem międzygałęziowym z gałęzi i do j,
Y_i - wartość produktu końcowego i-tej gałęzi,
A_j - wartość amortyzacji j-tej gałęzi,
x_0j - płace j-tej gałęzi,
Z_j - zysk j-tej gałęzi

Tablica1. Tablica przepływów międzygałęziowych

.

Wiersz TPM o numerze i,  i=1,2,..,n, obrazuje podział produktu wytworzonego w i-tej gałęzi. Popyt pośredni (zużycie pośrednie) obliczamy jako sumę przepływów "wychodzących" z tej gałęzi, czyli

      i=1,2,...,n            (1.1)

Produkt globalny i-tej gałęzi Xi ,rozpatrywany w kontekście podziału jest sumą popytu pośredniego i popytu końcowego ( inaczej: zużycia końcowego lub produktu końcowego), czyli

            i=1,2,...,n                      (1.2)

Zależność  ( 1.2) nosi nazwę równania produktu wytworzonego w i-tej gałęzi. Na przykład podział produktu globalnego drugiej gałęzi jest przedstawiony następująco:

Każda kolumna TPM opisuje proces tworzenia produktu w określonej gałęzi. Wielkości opisane w j-tej kolumnie składają się na bilans kosztów produkcji i zysków tej gałęzi. Na przykład, z drugiej kolumny można odczytać następujące koszty i zysk drugiej gałęzi:

Przedstawiony schemat wiąże się z równaniem kosztów j-tej gałęzi

       j=1,2,...,n             (1.3)

Sumując wartości produktu globalnego wszystkich gałęzi wyrażone równaniami podziału (1.2), a następnie wyrażone równaniami kosztów (1.3) i porównując obie sumy, otrzymujemy równanie równowagi ogólnej

                                        (1.4)

Sumę x_0j+Z_j , j=1,1,...,n, nazywa się wartością dodaną lub produkcją czystą j-tej gałęzi. Z równania (1.4) wynika, że łączna wartość dodana całego układu gospodarczego zwiększona o jego amortyzację jest równa łącznej wartości  produktu końcowego tego układu.

Na podstawie TPM można scharakteryzować technologię procesu produkcyjnego każdej z gałęzi. Do tego celu służą współczynniki kosztów

    i,j=1,2,...,n                                                (1.5)

zapisywane w postaci macierzy współczynników kosztów

                      (1.6)

Z definicji (1.5) wynika interpretacja współczynnika kosztów a_ij : w celu wytworzenia w j-tej gałęzi produktu o wartości 1 jp trzeba zużyć wyroby z i-tej gałęzi o wartości a_ij jp. Suma elementów j-tej kolumny macierzy A

        j=1,2,...,n                                          (1.7)

jest wartością współczynnika materiałochłonności j-tej gałęzi, ponieważ - zgodnie z interpretacją współczynników kosztów - oznacza wartość wyrobów ze wszystkich gałęzi, które trzeba zużyć w gałęzi j-tej , aby wytworzyć w tej gałęzi produkt o wartości 1 jp.

Jeżeli współczynnik materiałochłonności jakiejś gałęzi jest większy od jedności, to oznacza to, że koszty materiałowe tej gałęzi SA większe od wartości produktu globalnego gałęzi, a więc produkcja jest nieopłacalna.

Zauważmy ,że zgodnie ze wzorem (1.5) mamy

     oraz           z_ij=a_ijX_j       i,j=1,2,...,n                                                (1.8)

więc na podstawie macierzy struktury kosztów można, znając przepływy x_ij , wyznaczyć wartość produkcji globalnej i podobnie, znając wartości produkcji globalnej, można wyznaczyć wartości przepływów.

Tablica przepływów międzygałęziowych daje także możliwość wyznaczenia innych wskaźników potrzebnych do oceny i porównania efektywności ekonomicznej poszczególnych gałęzi i całego układu. Jest to na przykład, zysk jednostkowy, jednostkowa wartość dodana poszczególnych gałęzi i całej gospodarki oraz jeden z najważniejszych wskaźników, mianowicie rentowność będąca stosunkiem zysku do kosztu. Rentowność j-tej gałęzi jest dana wzorem

         j=1,2,...,n                                                   (1.9)

III. MODEL LEONTIEFA

Na podstawie równań podziału (1.2) o postaci:

        i=1,2,...,n                   

wprowadza się model przepływów międzygałęziowych, zwany modelem Leontiefa, opisujący występujące w rozpatrywanym układzie gospodarczym strukturalne zależności między produktem globalnym i produktem końcowym. Model ten ma postać równania macierzowego:

(I-A)X=Y                                                                                                            (1.10)

lub przy założeniu  det(I-A)
0,

(I-A)^-1=X,             gdzie                                                                                      (1.11)

        

są wektorami , odpowiednio, produktu globalnego i końcowego.

Macierz występująca w modelu Leontiefa

                         (1.12)

nosi nazwę macierzy Leontiefa. Element L_ij tej macierzy wyraża przyrost wartości produktu końcowego i-tej gałęzi spowodowany wzrostem o 1 j.p wartości produktu globalnego w j-tej gałęzi. Ponadto jest spełniona nierówność

      j=1,2,...,n                          (1.13)

Elementy macierzy (I-A)-1 występującej we wzorze (1.11) noszą nazwę współczynników pełnej materiałochłonności. Element tej macierzy zapisany w i-tym wierszu i j-tej kolumnie oznacza o ile musi wzrosnąć wartość produkcji globalnej w gałęzi o numerze i, aby uzyskać wzrost o 1 jp produktu końcowego gałęzi o numerze j przy nie zmienionym produkcie końcowym pozostałych gałęzi.

Model Leontiefa służy do wyznaczania, krótkookresowego prognozowania i symulacji wartości wektora produktu końcowego lub globalnego pod warunkiem, że zasadne jest założenie niezmiennej technologii produkcji, czyli stałych wartości elementów macierzy A.

Gdy w oparciu o model (1.10) wyznaczamy wektor produktu końcowego dla zadanego przyszłego wektora produktu globalnego, mamy do czynienia z prognozą I rodzaju. Gdy ustalony jest pożądany przyszły wektor produktu końcowego wówczas, na podstawie (1.11) wyznaczmy wektor produktu globalnego, który umożliwi osiągnięcie produktu końcowego na oczekiwanym poziomie. Taką prognozę określa się mianem prognozy II rodzaju. Ostatnim rodzajem prognozy wyznaczanej na podstawie modelu Leontiefa jest prognoza mieszana, która polega na prognozowaniu wybranych elementów wektora produktu globalnego i końcowego, jeśli ustalone są pozostałe elementy obu wektorów.

Z modelu Leontiefa w postaci (1.11) można korzystać również wtedy, gdy zamiast wektorów produktu globalnego X i produktu końcowego Y rozważa się wektory przyrostów

                

które oznaczają, odpowiednio, przyrost wartości produktu globalnego i końcowego w i-tej gałęzi.

Wówczas równania (1.10) i (1.11) przyjmują postać:

                                           (1.14)

IV. PRZYKŁADY ZASTOSOWANIA MACIERZY

Zadanie 1.

Gospodarka składająca się z trzecg gałęzi ma następującą tablice przepływów międzygałęziowych:

Xi		xij		Yi
500	20	30	100	350
600	40	60	100	400
800	50	120	280	350

Należy wyznaczyć macierz współczynników kosztów.

Rozwiązanie.

Najpierw wyznaczymy współczynniki kosztów dla pierwszej gałęzi:

b₁₁ =
b₂₁ =
b₃₁ =

Współczynniki kosztów dla drugiej gałęzi:

b₁₂ =
b₂₂ =
b₃₂ =

Współczynniki kosztów dla trzeciej gałęzi:

b₁₃ =
b₂₃ =
b₃₃ =
.

Macierz współczynników kosztów : B =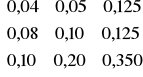

Odpowiedź - interpretacja:

Wyrazy pierwszej kolumny macierzy współczynników kosztów oznaczają, że do wytworzenia w pierwszej gałęzi produktu o jednostkowej wartości należy zużyć:

- produktu pierwszej gałęzi o wartości 0,04,

- produktu drugiej gałęzi o wartości 0,08,

- produktu trzeciej gałęzi o wartości 0,10.

Analogicznie można zinterpretować pozostałe kolumny macierzy. Sumy poszczególnych kolumn są współczynnikami materiałochłonności kolejnych gałęzi:

m₁ = 0,22 m₂ = 0,35 m₃ = 0,60 .

Współczynniki te są mniejsze od jedności, co oznacza , że produkcja jest opłacalna, bo wartość produktu globalnego gałęzi nie przekracza kosztów.

Zadanie 2.

  Gospodarka składa się z trzech gałęzi. Dana jest macierz współczynników kosztów i wektor wartości produktu globalnego:

B =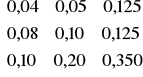
, X =

a) Należy wyznaczyć wektor wartości produktu końcowego

b) Jak zmienią się wartości produktu końcowego poszczególnych gałęzi, gdy wartość produkcji końcowej pierwszej gałęzi zmniejszy się o 100, drugiej zwiększy się o 200, natomiast trzeciej nie ulegnie zmianie?

c) O ile procent zmienią się wartości produktu końcowego poszczególnych gałęzi, gdy wartość produkcji globalnej pierwszej gałęzi zwiększy się o 15%, drugiej zwiększy się o 10%, a trzeciej zmniejszy się o 5%?

Rozwiązanie:

a) Wyznaczenie macierzy Leontiewa

b)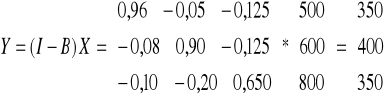

Otrzymaliśmy ∆X=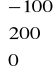
, i możemy skorzystać z modelu Leontiewa:

∆Y= (I-B)∆X =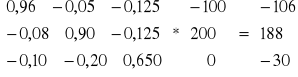

c) ∆X₁ =
= 75, ∆X₂ =
= 60, ∆X₃ =
= -40

∆X =
, ∆Y = (I-B)∆X =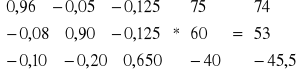

W punkcie a) obliczyliśmy, że Y =
, więc wartość produkcji końcowej :

pierwszej gałęzi wynosząca 350 wzrosła o 74 (czyli o
),

drugiej gałęzi wzrosła o
, a

trzeciej gałęzi zmalała o
.

Odpowiedź:

a) Y =
, b) Wartość produktu końcowego pierwszej gałęzi zmniejszy się o 106, drugiej powiększy o 188, natomiast trzeciej zmniejszy się o 30,

c) Wartość produktu końcowego pierwszej gałęzi zwiększy się o 21,14%, drugiej zwiększy się o 13,25%, trzeciej zmaleje o 13%.

 

 

14

---