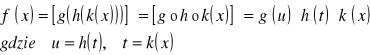Tadeusz Malinowski
Ewa Malinowska
grupa 106
Praca z Matematyki:
Badanie przebiegu funkcji
Teoria
Badanie przebiegu funkcji składa się z kliku elementów:
Określenie dziedziny funkcji badanej;
Znalezienie granic funkcji w nieskończoności oraz asymptot ukośnej, pionowych i poziomych;
Znalezienie miejsc zerowych (pierwiastków);
Policzenie pierwszej pochodnej - znalezienie maksimów i minimów funkcji
Sprawdzenie dziedziny dla pochodnej
Policzenie drugiej pochodnej - znalezienie punktów przegięcia, czyli miejsc gdzie funkcja zmienia monotoniczność;
Sporządzenie tabeli
Sporządzenie wykresu
Do określenia dziedziny funkcji potrzebujemy podstawowych wiadomości o funkcjach elementarnych. Są to takie informacje jak:
Mianownik nie może być równy 0
Liczba pierwiastkowana musi być większa od 0
Liczba logarytmowana musi być większa od zera, a dla jedności logarytm jest równy zero i nie może być w mianowniku
Dziedzina określa nam argumenty funkcji dla których funkcja nie istnieje czyli punkty które nie znajdą się na wykresie
np. ![]()
Później badamy granice funkcji. Podstawą jest badanie zachowania funkcji w +/- nieskończoności, a później w punktach nieznanych. Jeśli wiemy że funkcja nie istnieje w jakimś punkcie to powinniśmy sprawdzić jak zachowuje się otoczenie tego punktu, sprawdzamy to od strony liczb ujemnych i dodatnich. Często takie punkty okazują się asymptotami funkcji.
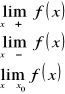
Następnie musimy sprawdzić czy funkcja nie ma asymptot, które bardzo potrafią ułatwić narysowanie funkcji.
Asymptota pionowa może być tylko w punktach, które określiliśmy w dziedzinie jako te, dla których funkcja nie istnieje. I jeśli dla takiego punktu przy badaniu granicy otrzymujemy, że wraz z x dążącym do tego punktu y dąży do +/- nieskończoności, to jest to asymptota pionowa.
Np.:
Podejrzewamy punkt a, wtedy
![]()
Mamy asymptotę x=a lewostronna.
![]()
Mamy asymptotę x=a prawostronna.
Jeśli spełnione są oba te warunki mamy asymptotę obustronną.
Asymptota pozioma występuje, jeśli przy sprawdzaniu granicy w nieskończoności otrzymujemy stałą.
![]()
Mówimy o asymptocie prawostronnej poziomej y=c.
![]()
Mówimy o asymptocie lewostronnej poziomej y=c
Podobnie jak wcześniej, występowanie obydwu warunków wskazuje na asymptotę obustronną w tym punkcie.
Asymptota ukośna wyrażona wzorem y=ax+b istnieje, jeśli spełnione jest równanie:
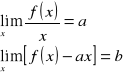
Warunkiem takiej sytuacji jest dziedzina funkcji zawierająca się w przedziale:
![]()
- asymptota prawostronna
![]()
- asymptota lewostronna
Jeżeli spełnione są obydwa warunki mamy asymptotę skośną obustronną
Pochodną funkcji w punkcie x nazywamy granicę ilorazu różnicowego tej funkcji, gdy przyrost argumentu h dąży do zera.
![]()
Licząc pochodną nie stosujemy samej definicji, tylko uproszczenia w postaci gotowych definicji na pewne funkcje elementarne i zbieżnych do nich twierdzeń. O ile nie będziemy przytaczali konkretnych funkcji elementarnych już z obliczoną pochodną, o tyle warto przytoczyć konkretne twierdzenia pozwalające z tych uproszczeń korzystać:
Obliczenie pierwszej pochodnej funkcji badanej pozwala na następujące stwierdzenia:
Jeśli w pewnym otwartym przedziale pochodna funkcji jest dodatnia, to w tym punkcie funkcja jest rosnąca
Jeśli jest ujemna, to badana funkcja jest malejąca
Jeśli jest równa zero, to w tym punkcie jest stała, i może to być minimum lub maksimum funkcji;
Czyli ekstremum funkcji to argument, dla którego pochodna przyjmuje wartość zero, a otoczenie lewostronne ma pochodną większą od 0, a prawostronne - mniejszą. W tym przypadku mówimy o maksimum funkcji.
Jeśli mamy sytuację odwrotną czyli, mamy argument, którego pochodna jest 0, a jego lewostronne otoczenie ma pochodną ujemną, a prawostronne dodatnią mówimy o minimum.
Jeśli policzymy drugą pochodną, czyli daną funkcję po zróżniczkowaniu ponownie zróżniczkujemy, to otrzymamy funkcję :
![]()
która określa nam następujące zależności:
jeśli f jest funkcją klasy C2 (czyli jest funkcją która w ogóle może być dwukrotnie różniczkowana) w przedziale (a; b) i jeżeli f''(x)>0 dla
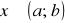
, to funkcja f jest wklęsła w tym przedziale;jeśli f jest funkcją klasy C2 (czyli jest funkcją która w ogóle może być dwukrotnie różniczkowana) w przedziale (a; b) i jeżeli f''(x)<0 dla
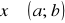
, to funkcja f jest wypukła w tym przedziale;punkt przegięcia jest jeśli f''(x)=0, i w prawostronnym sąsiedztwie f'' jest dodatnia, a w lewostronnym ujemna, lub odwrotnie;
Przykład
![]()
Dziedzina: ![]()
Granica: 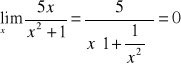
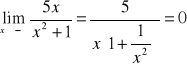
Miejsca Zerowe ![]()
Asymptoty Asymptoty ukośnej i pionowej brak
Mamy asymptotę obustronną poziomą, ale poza punktem (0,0)
1-sza pochodna 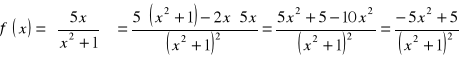
Szukamy ekstremów poprzez znalezienie miejsc zerowych,
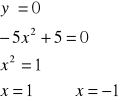
Czyli:
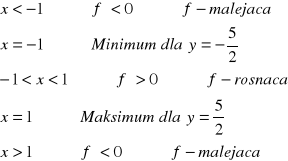
2-ga pochodna 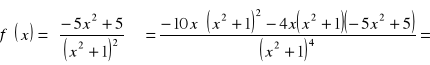
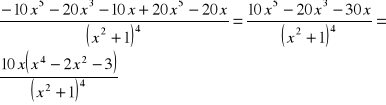
Porównujemy y'' do 0
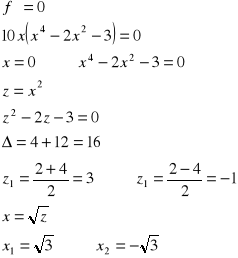
Ostatecznie otrzymujemy:
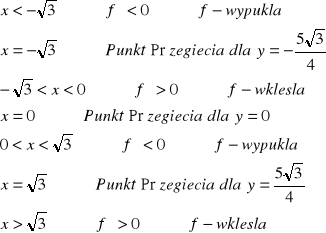
Tabelka
Wykres funkcji
Wyszukiwarka
Podobne podstrony:
Badanie funkcji, żywienie człowieka i ocena żywności, semestr 1, matematyka
matematyka zadania Gawinecki, WSEI, SEMESTR 2, Matematyka
Matematyka - wzory, WSEI, SEMESTR 2, Matematyka
Matematyka - PracaMalinowscy Macierze w ekonomii, WSEI, SEMESTR 2, Matematyka
Matematyka - Praca semestralna prawdopodobieństwo, WSEI, SEMESTR 2, Matematyka
Matematyka - PracaMalinowscy Prawdopodobieństwo, WSEI, SEMESTR 2, Matematyka
Matematyka - Praca Macierze w ekonomii, WSEI, SEMESTR 2, Matematyka
Matematyka - PracaMalinowscy Twierdzenia graniczne, WSEI, SEMESTR 2, Matematyka
Pochodna funkcji 3, PWR, semestr I, analiza matematyczna, materiały do nauki od DOROTY
Matematyka - Praca semestralna Twierdzenia graniczne, WSEI, SEMESTR 2, Matematyka
teoria funkcjonowania rynku ŚCIĄGA, WSEI, SEMESTR 0, teoria funkcjonowania rynku
MIKRO26, WSEI, semestr 1, Mikroekonomia
Sprawozdanie - Badania makroskopowe stali, I Semestr - Materialoznawstwo - sprawozdania
cwiczenie 1 badanie wlasnosci mechanicznych 1, Semestr 3 moje, wytrzymałość 4sem, LABORKI, LABORKI
Polityka Gospodarcza1, WSEI, SEMESTR 0, Polityka gospodarcza
Ćwiczenie nr 1. Badanie diody część 1, Semestr 4, Elektronika, Laboratorium
Testowanie, TEST Badania funkcjonalne
3 5 Badanie funkcji 2
więcej podobnych podstron