WOJSKOWA AKADEMIA TECHNICZNA
--------------------------------------------------------------------------------------------------------
LABORATORIUM FIZYCZNE
Grupa szkoleniowa C04J mgr inż. Andrzej WIŚNIEWSKI
stopień i nazwisko
prowadzącego
GOLONKA Marcin
ŁUKASZEWICZ Jarosław
( imię i nazwisko słuchacza)
ocena końcowa ocena przygot.
do ćwiczenia
SPRAWOZDANIE
Z
PRACY LABORATORYJNEJ Nr 21
Temat: Badanie drgań relaksacyjnych.
![]()
1.WSTĘP TEORETYCZNY
Celem ćwiczenia jest zapoznanie się ze zjawiskiem drgań relaksacyjnych w obwodzie elektrycznym. W ramach ćwiczenia ma nastąpić wyznaczenie pojemności nieznanego kondensatora - na podstawie uzyskanych wcześniej wyników z kondensatorami znanymi.
Drgania relaksacyjne to drganie, w których wzrosty i spadki napięć następują w sposób wykładniczy. Zazwyczaj (tak, jak w ćwiczeniu) do ich wytwarzania stosuje się proces ładowania i rozładowywania kondensatora rezystorem.
Po zamknięciu kluczem obwodu zawierającego: źródło siły elektromotorycznej E, rezystor R oraz kondensator C następuje ładowanie kondensatora. Korzystając z drugiego prawa Kirchhoffa otrzymamy:
Zważywszy, że
otrzymujemy równanie różniczkowe, które rozwiązujemy względem Q:
Obliczając pochodną dQ po dt otrzymujemy ostatecznie:
(1)-- napięcie na ładowanym kondensatorze.
Wielkość RC ma wymiar czasu i nazywa się stałą czasową obwodu, która jest równa czasowi, w jakim ładunek na kondensatorze powiększa się o czynnik 1-exp[-1].
Po naładowaniu kondensatora obwód łączymy tak, żeby nie zawierał źródła SEM. W takiej sytuacji będzie zachodziło rozładowywanie kondensatora rezystancją R.
Równanie obwodu ma postać:
Otrzymujemy równanie różniczkowe i rozwiązujemy je względem Q:
Wyznaczamy U:
(2)
Jest to napięcie na okładkach kondensatora przy jego rozładowywaniu.
Zależności napięcia na okładkach kondensatora od czasu dana jest wzorem
- podczas ładowania: )
- podczas rozładowywania: )
Cykliczne przełączanie klucza w obwodzie tak, aby kondensator już to ładował się, już to rozładowywał wymusi powstanie w obwodzie drgań relaksacyjnych. (W ćwiczeniu funkcję klucza spełnia neonówka).
Neonówka ma dwie elektrody pokryte warstwą metalu łatwo emitującego elektrony. Przy niwielkim napięciu na elektrodach prąd nie popłynie w neonówce. Po przekroczeniu wartości napięcia zapłonowego Uz przez lampę popłynie prąd o natężeniu ograniczonym tylko rezystancją zewnętrzną. Gdy napięcie na elektrodach spadnie poniżej napięcia gaśnięcia Ug lampa ponownie nie przewodzi prądu.
Czas t1 narastania napięcia na kondensatorze od Ug do Uz jest znacznie dłuższy od czasu jego opadania. Korzystając z powyższych zależności możemy wyznaczyć wartości t1 i t2.
oraz
. Rn-rezystancja neonówki
Okres drgań relaksacyjnych T=t1+t2.
Ponieważ t1>>t2 więcokres drgań w tym ćwiczeniu laboratoryjnym dany jest wzorem :
Uz - napięcie zapłonu neonówki; Ug - napięcie gaśnięcia
Poprzez podłączanie różnych oporników i kondensatorów otrzymamy całą rodzinę drgań relaksacyjnych. Możliwe będzie także znalezienie pojemności nieznanego kondensatora.
ILUSTRACJE:
Najprostszy układ służący do badania drgań relaksacyjnych:
Wykres drgań relaksacyjnych:
2.WYNIKI POMIARÓW
|
|
T1 [s] |
T2 [s] |
T3 [s] |
T4 [s] |
T5 [s] |
Tśr [s] |
R1 = 500
|
7,640 |
7,673 |
7,650 |
7,608 |
7,717 |
7,6576 |
7,640 |
|
10,343 |
10,414 |
10,450 |
10,306 |
10,318 |
10,3662 |
10,343 |
|
12,210 |
11,870 |
11,910 |
12,013 |
12,386 |
12,0778 |
12,210 |
|
16,418 |
16,855 |
16,973 |
17,074 |
17,048 |
16,8736 |
16,418 |
|
17,933 |
18,315 |
18,048 |
17,971 |
17,848 |
18,023 |
17,933 |
|
19,541 |
19,271 |
19,409 |
19,979 |
19,610 |
19,562 |
19,541 |
|
15,112 |
15,316 |
15,314 |
15,011 |
14,941 |
15,1388 |
15,112 |
R2 = 600 |
10,771 |
10,740 |
10,972 |
10,758 |
11,172 |
10,8826 |
10,771 |
|
14,010 |
14,172 |
14,212 |
14,335 |
14,453 |
14,2364 |
14,010 |
|
16,132 |
16,449 |
16,157 |
15,655 |
16,195 |
16,1176 |
16,132 |
|
21,209 |
21,206 |
21,451 |
21,318 |
21,452 |
21,3272 |
21,209 |
|
21,933 |
22,303 |
22,475 |
22,273 |
22,414 |
22,2796 |
21,933 |
|
24,056 |
23,739 |
23,746 |
23,971 |
23,953 |
23,893 |
24,056 |
|
18,717 |
18,211 |
18,177 |
18,111 |
18,477 |
18,3386 |
18,717 |
2.1 Wyniki obliczeń
Ri [kΩ] |
ā |
b |
Cx [nF] |
бā |
б b |
бTx |
бCx [nF] |
p |
ΔCx [nF] |
500 |
1,015 |
1,984 |
12,964 |
0,004 |
0,054 |
0,154 |
0,706 |
0,98 |
1,642 |
600 |
1,100 |
4,992 |
12,130 |
0,021 |
0,265 |
0,227 |
3,225 |
0,98 |
7,501 |
3.WYLICZENIA
3.1 Wykresy
3.2 Obliczam współczynniki prostych aproksymowanych.
Wykorzystuje wzory:
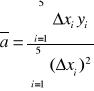
, ![]()
x - kolejne wartości pojemności
y - kolejne wartości okresów
Dla R1:
![]()
![]()
![]()
![]()
![]()
Dla R2:
![]()
![]()
![]()
![]()
3.3 Obliczam odchylenia standardowe.
Wykorzystuje wzory:
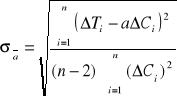
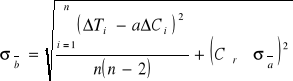
ΔCi = Ci - Cśr, ΔTi = Ti - Tśr
Dla R1:
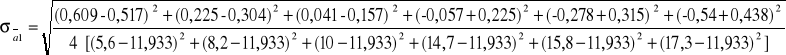
![]()
Analogicznie:
![]()
Dla R2:
![]()
![]()
3.4 Obliczam wartość nieznanej pojemności.
Wykorzystuje wzór:
![]()
Dla R1:
![]()
Dla R2:
![]()
3.5 Obliczam błąd średni kwadratowy.
Wykorzystuje wzór:
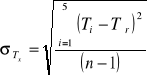
Dla R1:
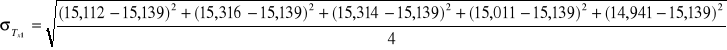
![]()
Dla R2:
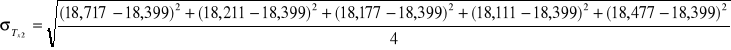
![]()
3.6 Obliczam błąd średni kwadratowy.
Wykorzystuje wzór:
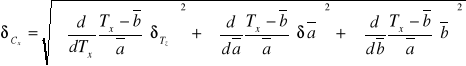
Dla R1:
![]()
Dla R2:
![]()
3.7 Obliczam przedział ufności.
Wykorzystuje wzór:
![]()
kp=2,236
Dla R1:
![]()
Dla R2:
![]()
4.WNIOSKI
Z wyników pomiarów wywnioskowaliśmy, iż pojemność szukana jest równa co do wartości średniej arytmetycznej wartości pojemności kondensatorów, na których przeprowadzano doświadczenie laboratoryjne. Dla obu wartości oporności są one jednakowe. Osiągnięcie takiego wyniku było możliwe ze względu na dokładności aparatury pomiarowej (należy nadmienić , iż jest ona całkowicie wolna od ewentualnych błędów „ludzkich”). Należałoby także zaznaczyć fakt, iż wyniki otrzymane podczas badania laboratoryjnego nie pokrywają się z wynikami otrzymanymi przez inny zespół na tym samym zestawie rezystorów. Przypuszczamy, iż przyczyna zaistniałego stanu mogła być inna wartość temperatury obwodu (obwód był wcześniej używany, co mogło doprowadzić do wzrostu jego temperatury), mająca wpływ na wartości poszczególnych wielkości charakteryzujących układ wykorzystywany podczas doświadczenia badania drgań relaksacyjnych.
Wyszukiwarka
Podobne podstrony:
lab 21, Notatki, FIZYKA, SEMESTR II, laborki, lab
lab 13, Notatki, FIZYKA, SEMESTR II, laborki, lab
Lab 28, Notatki, FIZYKA, SEMESTR II, laborki, lab
Lab 15, Notatki, FIZYKA, SEMESTR II, laborki, lab
Lab 31, Notatki, FIZYKA, SEMESTR II, laborki, lab
Lab 9, Notatki, FIZYKA, SEMESTR II, laborki, lab
Lab fizyki, Notatki, FIZYKA, SEMESTR II, laborki, lab
Lab 12, Notatki, FIZYKA, SEMESTR II, laborki, lab
M07 - sprawozdanie-ewela, Notatki, FIZYKA, SEME
IV WYNIKI TEORETYCZNE, Notatki, FIZYKA, SEMESTR II, laborki, laborki fizyka II sem - ewel+jarecki, P
1231231231231, Notatki, FIZYKA, SEMESTR II, laborki, laborki fizyka II sem - ewel+jarecki, pierdoły
Twierdzenie Steinera, Notatki, FIZYKA, SEMESTR II, laborki, laborki fizyka II sem - ewel+jarecki, pi
Wnioski do spr z elektry 3, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Lab. Ukł. Napędowych
ProtokółN2, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Lab. Ukł. Napędowych
Wnioski e1, PW SiMR, Inżynierskie, Semestr V, syf, laborki, Lab. Ukł. Napędowych, sprawko napedy
więcej podobnych podstron