FUNKCJE WIELU ZMIENNYCH

I ICH ZASTOSOWANIA

DEFINICJA

Funkcją n zmiennych nazywamy odwzorowanie:

Alternatywny zapis ma postać:

gdzie:

GRANICA FUNKCJI

DEFINICJA

Ciąg punktów {P_k}, dla k=1,2,... dąży do punktu P₀, czyli:

gdy odległość d(P_k,P₀) dąży do zera przy k→∞.

Zachodzi to wtedy i tylko wtedy, gdy jednocześnie:

.

DEFINICJA (granicy funkcji wg Heinego)

Funkcja f(P) ma w punkcie P₀ granicę g, jeśli dla każdego ciągu punktów {P_k} różnych od P₀, dążącego do P₀, odpowiedni ciąg wartości funkcji {f(P_k)} dąży do liczby g.

jeżeli g jest liczbą skończoną - granica właściwa, jeżeli g→∞ - granica niewłaściwa.

Przykład 1

Obliczyć granice funkcji:

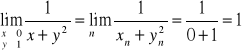
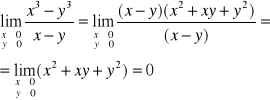
CIĄGŁOŚĆ FUNKCJI

DEFINICJA

Funkcję f(P)=f(x₁, x₂, ...,x_n) nazywamy ciągłą w punkcie

P₀(x₁⁰, x₂⁰, ...,x_n⁰) jeżeli:

Funkcja jest ciągła w punkcie, jeżeli:

1. istnieje f(P₀),

2. istnieje
   ,

3. 
   

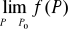
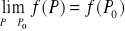
Przykład 2

Zbadać ciągłość funkcji:

w punkcie P₀(1,1).

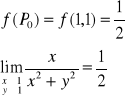
Funkcja jest ciągła.

POCHODNE CZĄSTKOWE

DEFINICJA

W obszarze otwartym D dana jest funkcja f(x₁,x₂,...,x_n) określona w otoczeniu punktu P₀(x₁⁰, x₂⁰, ...,x_n⁰).

Jeżeli wszystkim zmiennym x₁,x₂,...,x_i-1,x_i+1,...,x_n nadamy wartości stałe (x_j⁰), to funkcja f zależeć będzie tylko od zmiennej x_i.

Pochodną tak utworzonej funkcji jednej zmiennej f(x₁⁰,x₂⁰,...,x_i,...,x_n⁰) w punkcie x_i=x_i⁰ nazywamy pochodną cząstkową funkcji f(x₁,x₂,...,x_n) względem zmiennej x_i w punkcie P₀ i oznaczamy symbolem:

lub
.

Pochodna cząstkowa jest granicą ilorazu różnicowego:

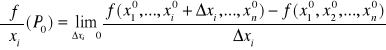
Definicje pochodnych cząstkowych dla funkcji f(x,y):

Pochodne cząstkowe rzędu drugiego:

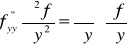
Pochodne mieszane (krzyżowe):

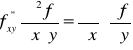
Funkcja n zmiennych ma n² pochodnych cząstkowych rzędu drugiego.

Analogicznie obliczane są pochodne wyższego rzędu.

TWIERDZENIE SCHWARZA

Jeżeli funkcja f(x,y) posiada w punkcie P₀(x₀,y₀) i pewnym jego otoczeniu pochodne cząstkowe f_x^', f_y^', f_xy^'' i jeżeli pochodna f_xy^'' jest ciągła w punkcie P₀, to w tym punkcie istnieje pochodna cząstkowa f_yx^'' i jest równa f_xy^'', to znaczy:

Przykład 3

Obliczyć pochodne cząstkowe funkcji:

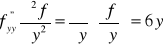
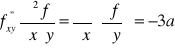
RÓŻNICZKA ZUPEŁNA

Dla funkcji jednej zmiennej różniczka funkcji f(x) w punkcie x₀ i dla przyrostu Δx zmiennej niezależnej jest wyrażeniem postaci:

Różniczkę zmiennej niezależnej można identyfikować z różniczką funkcji y = x i wówczas:

więc

Różniczka funkcji y = f(x) w punkcie P(x₀) ma postać:

Przyrostem funkcji w punkcie P₀(x₁⁰,...,x_n⁰) i w punkcie P₁(x₁⁰+Δx₁,...,x_n⁰+Δx_n) nazywamy różnicę tych wartości.

Funkcję f(x₁,...,x_n) nazywamy różniczkowalną w punkcie P₀(x₁⁰,...,x_n⁰), jeżeli przyrost funkcji w tym punkcie może być przedstawiony w postaci:

gdzie:

A₁,...,A_n - stałe,

ε(Δx₁,...,Δx_n) - dąży do zera, gdy:

Jeżeli funkcja f(x₁,...,x_n) jest różniczkowalna w punkcie P₀, to wyrażenie:

nazywamy różniczką zupełną funkcji f w tym punkcie i oznaczamy ją symbolem:

TWIERDZENIE

Funkcja f(x₁,...,x_n) jest różniczkowalna w punkcie P₀, to:

Wobec faktu, że dla zmiennych niezależnych zachodzi:

Powyższy wzór na różniczkę zupełną możemy zapisać w postaci sumy różniczek cząstkowych funkcji n zmiennych:

TWIERDZENIE

Jeżeli funkcja f(x₁,...,x_n) posiada pochodne cząstkowe w pewnym otoczeniu punktu P₀(x₁⁰,...,x_n⁰) i jeżeli pochodne te są ciągłe w punkcie P₀, to funkcja f(x₁,...,x_n) jest w tym punkcie różniczkowalna.

Przykład 4

Znaleźć różniczkę zupełną I-go rzędu funkcji:

RÓŻNICZKI ZUPEŁNE WYŻSZYCH RZĘDÓW

Różniczkę zupełną I-go rzędu można zapisać w postaci ogólnej:

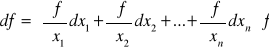
Różniczka zupełna rzędu k ma postać:

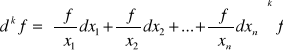
Przykład 5

Obliczyć różniczkę zupełną drugiego rzędu funkcji:

Różniczka zupełna rzędu II ma postać:

EKSTREMA FUNKCJI WIELU ZMIENNYCH

DEFINICJA

Funkcja f(x,y) określona w otoczeniu K punktu P₀(x₀,y₀) ma w tym punkcie maksimum (minimum) lokalne, jeżeli istnieje takie sąsiedztwo S⊂K punktu P₀, że zachodzi:

dla maksimum
,

dla minimum
,

dla każdego (x,y)∈S.

TWIERDZENIE

Jeżeli dana jest funkcja dwóch zmiennych f(x,y) mająca w otoczeniu punktu P₀ wszystkie drugie pochodne cząstkowe ciągłe oraz jeżeli spełnione są następujące warunki:

1. 
   ,

2. 
   

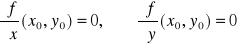
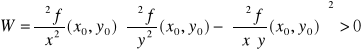
to w punkcie P₀ funkcja f ma ekstremum:

maksimum, jeżeli:

minimum, jeżeli:

Jeżeli w punkcie P₀ istnieje ekstremum, to pochodne cząstkowe drugiego rzędu w tym punkcie są takiego sa,ego znaku.

Jeżeli W<0, to funkcja f(x,y) nie ma w tym punkcie ekstremum.

Jeżeli W=0, to przypadek jest wątpliwy i wymaga specjalnego badania.

Przykład 6

Zbadać ekstrema funkcji:

Obliczamy pochodne

Należy rozwiązać układ równań:

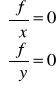
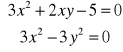
Otrzymujemy cztery rozwiązania: P₁(1,1), P₂(1,1), P₃(
,-
), P₄(-
,
).

Podstawiamy do wzoru na wyróżnik W.

(1)

(2)

(3)

(4)

Ponieważ

w punkcie P₃ jest minimum oraz

w punkcie P₄ jest maksimum.

NAJWIĘKSZA I NAJMNIEJSZA WARTOŚĆ FUNKCJI

TWIERDZENIE

Funkcja f(x₁,...,x_n) ciągła w pewnym obszarze D domkniętym i ograniczonym musi przyjmować w tym obszarze wartość najmniejszą i największą, przy czym te wartości są bądź ekstremami lokalnymi, leżącymi wewnątrz obszaru D, bądź występują na brzegu obszaru.

Aby znaleźć te wartości:

1. Sprawdzamy w danym obszarze znajdują się ekstrema lokalne, jeśli tak to wyznaczamy ich wartości.

2. Wyznaczamy największą i najmniejszą wartość badanej funkcji na brzegu obszaru D.

3. Porównujemy wartości otrzymane w punkcie 1 i 2.

Przykład 7

Znaleźć największą i najmniejszą wartość funkcji:

w obszarze x ≤ 0, y ≤ 0,x+y ≥ -3.

Wyznaczamy punkty wewnątrz obszaru:

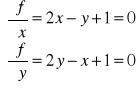
stąd x = -1 i y = -1.

Obszar ma postać:

(-3,0) (0,0)

(0,-3)

Wartość funkcji w punktach:

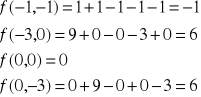
WYPUKŁOŚĆ I WKLĘSŁOŚĆ FUNKCJI

Niech symbol W oznacza podzbiór wypukły przestrzeni Rⁿ oraz niech funkcja f(x₁,...,x_n) ciągła w zbiorze W.

Funkcja f jest wypukła (wklęsła) w zbiorze W, jeżeli dla każdych dwóch punktów P₁(x₁¹,...,x_n¹), P₂(x₁²,...,x_n²) należących do zbioru W, mamy:

lub

I własność

Jeżeli funkcja f jest w zbiorze W wypukła, to funkcja -f jest w tym zbiorze wklęsła.

II własność

Wszystkie punkty wewnętrzne odcinka łączącego punkty f(P₁) i f(P₂) wykresu leżą powyżej powierzchni z=f(x₁,...,x_n) lub na niej dla funkcji wypukłej oraz leżą poniżej tej powierzchni dla funkcji wklęsłej.

Niech funkcja f ma w zbiorze W ciągłe pochodne pierwszego i drugiego rzędu. Wtedy w każdym punkcie P∈W istnieje różniczka zupełna d²f postaci:

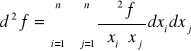
TWIERDZENIE

Jeżeli dla każdego P∈W, wartość d²f jest dodatnia (ujemna), to funkcja f jest w zbiorze W ściśle wypukła (wklęsła).

TWIERDZENIE

Jeżeli dla każdego P∈W, wartość d²f jest nieujemna (niedodatnia), to funkcja f jest w zbiorze W wypukła (wklęsła).

Przykład 8

Funkcja produkcji Cobba-Douglasa opisuje zależność pomiędzy produkcją a nakładami czynników produkcji

Własności funkcji C-D:

1. jednorodna stopnia (α+β),

2. izokwanty mają ujemne nachylenie,

3. ściśle wypukła dla dodatnich K i L.

Dla α+β=1 funkcja C-D jest liniowo jednorodna co oznacza że wystąpią stałe przychody skali.

Efekt skali: rosnący, stały, malejący.

Funkcja jest jednorodna stopnia r, jeżeli pomnożenie każdego z jej argumentów przez stałą j spowoduje zmianę wartości funkcji w proporcji j^r, to znaczy jeśli:

.

Własności liniowo jednorodnej funkcji produkcji:

Własność I

Dla danej liniowo jednorodnej funkcji produkcji Q=f(K,L) przeciętny produkt pracy w jednostkach fizycznych i przeciętny produkt kapitału w jednostkach fizycznych są funkcjami ilorazu kapitału i pracy k≡K/L.

Produkty przeciętne są funkcjami tego samego k.

Własność II

Gdy dana jest liniowo jednorodna funkcja produkcji Q=f(K,L), wówczas krańcowe produkty w jednostkach fizycznych mogą być wyrażone jako funkcje tego samego k.

Produkty krańcowe są funkcjami tego samego k.

Własność III (twierdzenie Eulera)

Jeżeli Q=f(K,L) jest liniowo jednorodna, to:

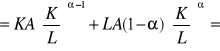
Przykład

Firma produkuje dwa wyroby w warunkach doskonałej konkurencji. Co oznacza, że ceny tych wyrobów są zmiennymi niezależnymi (tzw. zmienne egzogeniczne).

Funkcja przychodu firmy:

gdzie x_i reprezentuje poziom produkcji i-tego produktu.

Funkcja kosztu firmy:

Koszt krańcowy pierwszego(drugiego) wyrobu jest funkcją x₁ i x_2.

Funkcja zysku firmy:

Maksymalizacja zysku:

Rozwiązując otrzymujemy:

Zastosowania matematyki w ekonomii Funkcje wielu zmiennych

5

---