POLITECHNIKA GDAŃSKA

WYDZIAŁ BUDOWNICTWA LĄDOWEGO

PROJEKT

ŚCIANKI SZCZELNEJ

JEDNOKROTNIE ZAKOTWIONEJ

	Projektant:	Data	Podpis
	Rafał Robert Lipiński KBI-1
	Uwagi:

Spis treści

1.0. Opis techniczny

Tematem projektu jest wstępne zaprojektowanie ścianki szczelnej jednokrotnie zakotwionej, która ma za zadanie odgradzać i zabezpieczać brzeg rzeki.

Ścianka szczelna wykonana jest z brusów stalowych typu Larssena V.

Wbijanie ścianki szczelnej zaczyna się od narożnika. Bursy stalowej ścianki szczelnej należy wbijać zawsze wcześniej przygotowanymi na placu budowy parami. Kolejno należy wbijać następne pary na odcinku wytyczonym drewnianymi prowadnicami ułożonymi na ziemi o długości 4-5 m o rozstawie równym wielokrotności szerokości bursu. W celu wyrównania powstałych w czasie wbijania pochyleń bursów należy je naprostować specjalnym bursem o kształcie klinowym. Aby uniknąć zniekształcenia bursu od bezpośrednich uderzeń kafaru na brusy zakłada się kołpaki na glowice złączonych bursów.

Do wbijania najlepiej wykorzystać dwa kafary. Jeden wbija brusy na 2-4 m, drugi w odstępie 4-5 m za pierwszym wbija na właściwą głębokośc - 15,00m.

Po wbiciu ostatniego należy wykonać odkop po obu stronach profilu tuż przy ściance na 1,6 m w celu zamocowania kleszczy, które składają się z dwóch ceowników C180. Do zamocowania stosuje się śruby M20 w odstępach 0,84 m. Grunt z wykopu wykorzystywany jest jako grunt naypowy.

W odstępach 1,68 mocuje się ściąg wykonany z pręta o średnicy 50 mm. W miejscu ogwintowania powinien być spęczniony w celu utrzymania minimalnej zaprojektowanej średnicy. Przed zamocowaniem ściągu należy wykonać wykop wąskoprzestrzenny na pręt ściagu.

Wykop do umieszczenia płyt kotwiących należy wykonać w dwóch rzędach naprzemiennie w odległości 18,9 m i 27,4m od ścianki. Na ściąg zakładamy nakrętki napinające (śruby rzymskie) w odległościach odpowiednio: 16,4 i 19,1 m od ścianki szczelnej.

Po zamocowaniu ściagu zasypujemy wykop na płytę i mocowanie kleszczy oraz zagęszczamy grunt. Następnie za pomocą śruby rzymskiej naciągamy ściąg. Gdy zaobserwujemy dostateczny opór zasypujemy wykop ze śrubą rzymską.

Po wykonaniu powyższych czynności można odkopać ścianę od strony rzeki.

2.0. Obliczenie sił parcia i odporu.

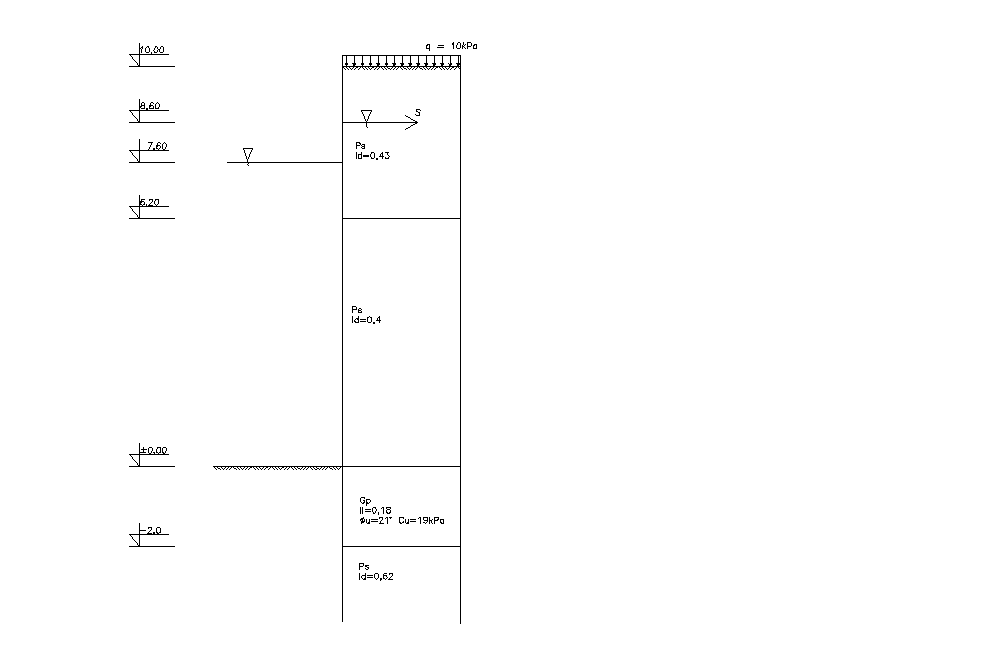
2.1. Wyznaczenie parametrów geotechnicznych.

Parametry		Piasek średni	Piasek średni	Glina piaszczysta	Piasek średni
		Warstwa 1	Warstwa 2	Warstwa 3	Warstwa 4
ID/IL	-	0,43	0,40	0,18	0,62
ρ	[g/cm^3]	1,85	2	2,2	2
ρs	[g/cm^3]	2,65	2,65	2,67	2,65
w	[%]	14	22	12	22
φu^(n)	[^o]	32,5	32,4	^21	33,7
c u^(n)	[kPa]	-	-	19	-
γ^(n)	[kN/m^3]	18,13	19,6	21,56	19,6
n	[-]	0,38	0,38	0,26	0,38
ρ'	[g/cm^3]	1,01	1,02	1,22	1,02
γ'	[kN/m^3]	9,90	10,00	12,04	10,00

Ciężar objętościowy gruntu pod zwierciadłem wody gruntowej policzono wg. wzorów :

ρ'= (1-n)·(ρ_s-ρ_w)

γ'=ρ'·9,81

2.2. Wyznaczenie współczynników odporu i parcia gruntu.

2.2.1. Współczynniki odporu.

Wzór na współczynnik według normy PN-83/B-03010:

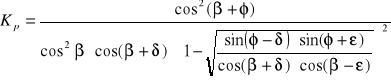
gdzie:

β - kąt nachylenia ściany do pionu; β= 0;

ε - kąt nachylenia naziomu do poziomu; ε = 0;

δ - wartość charakterystyczna kąta tarcia gruntu o ścianę.

	Warstwa 3	Warstwa 4
	Gp	Ps
δ =	-φ	-φ/2
Kp =	3,83	6,60

Współczynnik odporu dla gliny redukujemy o 30 %:

K_p `= K_p x 0,7= 3,83x0,7 = 2,68

Współczynnik odporu dla piasku redukujemy o 15%:

K_p `= K_p x 0,85= 6,6 x 0,85= 5,61

2.2.2. Współczynnik parcia.

Wzór na współczynnik według normy PN-83/B-03010:

K_a= tg ²(45^o - φ/2)

	Warstwa 1	Warstwa 2	Warstwa 3	Warstwa 4
	Ps	Ps	Gp	Ps
φ	32,5	32,4	21	33,7
Ka	0,301	0,302	0,472	0,286

2.3. Wyznaczenie wartości parcia i odporu na spągach i stropach warstw.

2.3.1. Wyznaczenie wartości parcia na spągach i stropach warstw.

e_a=(γ_f1 ·q_z + γ_i · z · γ_f2) · K_a -
· γ_f2 + γ_{f3 ­}· e_w

gdzie:

q_z - zastępcze obciążenie naziomu; q_z=q_n+
;

γ_i - wartość ciężaru objętościowego poszczególnych warstw;

K_a - współczynnik parcia;

c^(r) - obliczeniowa spójność gruntu, c^(r) =0,5·c

e_w - parcie hydrostatyczne.

γ_fi - współczynniki obciążenia

Rodzaj gruntu	Rodzaj parcia		Obciążenie naziomu
		czynne		odpór
Zasypowe niespoiste	1,20	0,80		>5,0 γf =1,2
Rodzime niespoiste	1,10	0,87
Rodzime średniospoiste	1,20	0,80
Parcie wody γf =1,1

Róznica poziomów wody z obu stron ścianki wynosi 1m, stąd więc e_w= 1·1·9,81 = 9,81 [kN/m²]

Warstwa	γ^(n)/γ'	φu^(n)	Ka	Głębokość zi	Zastępcze obciążenie naziomu qz=qn+∑γ·hi	qz­­­· Ka	γi · z · Ka	2·c^(r)·√Ka	ew	ei
Ps /nad wodą/	18,13	32,50	0,30	0,00	10,00	3,01	0,00	-	-	3,31
Ps /nad wodą/	18,13	32,50	0,30	1,40	10,00	3,01	7,64	-	-	11,71
Ps /pod wodą/	9,90	32,50	0,30	0,00	35,38	10,65	0,00	-	-	11,71
Ps /pod wodą/	9,90	32,50	0,30	1,00	35,38	10,65	2,98	-	9,81	25,78
Ps /pod wodą/	9,90	32,50	0,30	2,40	35,38	10,65	7,15	-	9,81	30,37
Ps /pod wodą/	10,00	32,40	0,30	0,00	59,15	17,88	0,00	-	9,81	30,45
Ps /pod wodą/	10,00	32,40	0,30	6,20	59,15	17,88	18,74	-	9,81	51,07
Gp /pod wodą/	12,04	21,00	0,47	0,00	121,17	57,23	0,00	13,06	9,81	58,08
Gp /pod wodą/	12,04	21,00	0,47	2,00	121,17	57,23	11,37	13,06	9,81	71,73
Ps /pod wodą/	10,00	33,70	0,29	0,00	145,25	41,58	0,00	-	9,81	56,53
Ps /pod wodą/	10,00	33,70	0,29	5,00	145,25	41,58	14,32	-	9,81	72,29
	[kN/m^3]	[^o]	[-]	[m]	[kN/m^2]		[kN/m^2]		[kN/m^2]	[kN/m^2]

2.3.2. Wyznaczenie wartości odporu na spągach i stropach warstw.

e_p=(q_z · γ_f1­ + γ_i · z · γ_f2­) · K_p +
· γ_f2­

gdzie:

q_z- zastępcze obciążenie naziomu; q_z=q_n+
;

γ_i - wartość ciężaru objętościowego poszczególnych warstw;

K_p -współczynnik parcia.

γ_fi - współczynniki obciążenia

Warstwa	γ^(n)/γ'	Kp	Głębokość zi	Zastępcze obciążenie naziomu qz=qn+∑γ·hi	qz · Kp	γi · z · Kp	2·c^(r)·√Kp	ep
Gp /pod wodą/	12,04	3,84	0,00	0,00	0,00	0,00	37,23	29,78
Gp /pod wodą/	12,04	3,84	2,00	0,00	0,00	92,44	37,23	103,73
Gp /pod wodą/	10,00	6,61	0,00	24,08	159,09	0,00	-	190,90
Ps /pod wodą/	10,00	6,61	5,00	24,08	489,51	330,42	-	884,79
	[kN/m^3]	[-]	[m]	[kN/m^2]		[kN/m^2]		[kN/m^2]

3.0. Wyznaczenie wartości R_a, t, M_max

3.1. Podzielenie ściany na paski i określenie wypadkowych parcia i odporu w poszczególnych paskach.

Znak „-„ oznacza odpór.

Nr paska	hi paska	ei	ei+1	0,5xhi·(ei+ei+1)
1	0,7	3,31	7,51	3,79
2	0,7	7,51	11,71	6,73
3	1	11,71	25,78	18,75
4	0,7	25,78	28,08	18,85
5	0,7	28,08	30,37	20,46
6	0,775	30,45	33,03	24,60
7	0,775	33,03	35,61	26,60
8	0,775	35,61	38,19	28,60
9	0,775	38,19	40,76	30,59
10	0,775	40,76	43,34	32,59
11	0,775	43,34	45,92	34,59
12	0,775	45,92	48,50	36,59
13	0,775	48,50	51,07	38,58
14	0,94	58,08	0,00	27,30
15	1,06	0,00	-32,00	-16,96
16	0,5	-134,37	-162,53	-74,23
17	0,5	-162,53	-190,69	-88,31
18	0,5	-190,69	-218,86	-102,39
19	0,5	-218,86	-247,02	-116,47
20	0,5	-247,02	-275,18	-130,55
21	0,5	-275,18	-303,35	-144,63

3.2. Z wypadkowych parcia i odporu wykreślono wielobok.

Przyjęto H = 150 [kN] wg. rysunku konstrukcyjnego.

3.3. Z wieloboku sił wykreślono wykres momentów i określono m_max.

3.4. Wykreślono zamykającą z punktu przecięcia pierwszego promienia wieloboku sznurowego z poziomem kotwy tak aby bezwzględna różnica momentów wynosiła mniej niż 10%.

3.5. Wyznaczono linię ugięcia przez wypadkowe siły fikcyjne:

Nr paska	hi paska	fi	fi+1	Fi=0,5·hi·(fi+fi+1)
1	0,50	0	49,54	12,39
2	0,85	49,54	123,09	73,37
3	0,70	123,09	174,11	104,02
4	0,74	174,11	215,76	143,76
5	0,78	215,76	245,79	178,85
6	0,78	245,79	261,05	196,40
7	0,78	261,05	260,5	202,10
8	0,78	260,5	243,11	195,15
9	0,78	243,11	207,85	174,75
10	0,78	207,85	153,69	140,10
11	0,78	153,69	79,59	90,40
12	0,75	79,59	0	29,69
13	1,28	0	137,3	87,87
14	0,60	137,3	169,31	91,98
15	0,50	169,31	166,38	83,92
16	0,50	166,38	129,32	73,93
17	0,50	129,32	53,44	45,69
18	0,22	53,44	0	5,88

Zbudowano z nich wielobok sznurowy i wykreślono linię ugięcia, ponieważ przemieszczenie ścianki w miejscu zakotwienia jest różne od zera wyznaczono:

gdzie :

s = 1,775m

R= 12,9 m

H₁ = 5 m

Skorygowano położenie zamykającej.

3.6. Przeniesiono równolegle zamykającą na pierwszy wielobok sił i wyznaczono wartość R_a.

R_a = 170,80 [kN]

4.0. Wyznaczenie głębokości wbicia ścianki szczelnej.

t = u + 1,2·x

gdzie:

u - głębokość na jakiej wartość parcia jest równa odporowi;

x - odległość od punktu wyrównania się parcia i odporu do spodu paska gdzie przecina wielobok sznurowy zamykająca.

Wartości u i x odczytano z rysunku - brak możliwości obliczenia punktu zerowego:

u = 0,94 [m]

x = 3,31 [m]

t = 4,912 [m]

Przyjęto 5,00 [m], a więc cała wysokość ścianki wynosi 15,00 [m].

5.0. Przyjęcie przekroju ścianki.

Główne założenie: profile typu Larssena ze stali St3S.

M_max= m_max · H

Potrzebny wskaźnik wytrzymałości ścianki na 1 mb wyznacza się ze wzoru:

W_x=

gdzie:

­­f­_d - wytrzymałość obliczeniowa stali na rozciąganie; f_d=150 [MPa]

Wartości H i m_max odczytano z rysunku:

m_max= 2,00 [m]

H = 150 [kN]

M_max= 300 [kNm]

W_x=0,002 [m³]

W_x = 2000 [cm³]

Przyjęto profil IVn o W_x = 2200 [cm³] i szerokości bursa B = 0,40 [m], a długości 15,00 [m].

Sprawdzenie warunku:

gdzie:

m - współczynnik bezpieczeństwa; m=1,2.

[MPa]

[MPa]

Warunek niespełniony.

Przyjęto nowy profil V o W_x = 3000 [cm³] i szerokości bursa B = 0,42 [m], a długości 15,00 [m].

Sprawdzenie warunku:

gdzie:

m - współczynnik bezpieczeństwa; m=1,2.

[MPa]

[MPa]

Warunek spełniony.

Ostatecznie przyjeto profil Larssena V.

6.0. Obliczenie ściągu.

Przyjęto ściąg nie nachylony co 4 bursy ze stali 18G2.

Potrzebny przekrój ściągu oblicza się ze wzoru :

gdzie:

R_a -reakcja w ściągu;

a - rozstaw kotew;

α - nachylenie ściągu;

_­f_d - wytrzymałość obliczeniowa na rozciąganiedla stali, z której projektowana jest kotew.

R_a = 170,8 [kN]

a = 1,68 [m] - co 4 bursy

f_d = 200000 [kN/m²]

A_s = 14,34 [cm²]

Obliczenie średnicy:

d = 4,27 [cm]

Przyjęto pręt o średnicy d = 45 [mm] .

Sprawdzenie warunku:

gdzie:

m - współczynnik bezpieczeństwa; m=1,2;

A_s' - pole przekroju przyjętego pręta.

A'_s = 15,9 [cm²]

1804,67 [kN]= 180,46 [MPa]

=166,66 [MPa]

Warunek niespełniony.

Z powodu niespełnienia warunku zwiększono średnicę ściągu do d= 50 [mm].

Ponowne sprawdzenie warunku:

Przyjęto pręt o średnicy d = 50 [mm] .

Sprawdzenie warunku:

A'_s = 19,36 [cm²]

1461,7 [kN]= 146,17 [MPa]

=166,66 [MPa]

Warunek spełniony

Ostatecznie przyjęto ściąg o średnicy φ 50 [mm]

7.0. Obliczenie kleszczy.

Kleszcze składają się z układu dwóch ceowników oddalonych od siebie o średnicę ściągu 5,0 [cm].

Przyjęto rozmieszczenie płyty kotwiącej co cztery bursy.

l_s = a·B = 1,68 [m]

M_max= 0,1·R_a·l_s²

M_max = 48,20 [kNm]

W'_x = 255 [cm³]

Przyjęto na kleszcze układ dwóch ceowników C180 o W_x= 300 > 255 [cm³]

8.0. Obliczenie śrub mocujących.

Przyjęto rozstaw śrub co drugą bursę więc:

b = 0,84 [m]

Siła rozciągająca:

S' = b·R_a / l­_a = 85,4 [kN]

Na podstawie PN90/B-03200

Przyjęto śruby klasy 5,8 o wytrzymałości:

R_m= 52 [kN/m²] R_e= 42,5 [kN/m²]

A_s = min(
) = 2,36

A_s = 2,36 [cm²]

Przyjęto śruby M20 o przekroju czynnym 2,45.

9.0. Obliczanie płyty kotwiącej (metoda Buchholza).

Q_r< m · Q_f

gdzie:

m- współczynnik bezpieczeństwa; m =0,8

Q_r= R_a·l_s +E_a·b

Q_f = Z_pgr

Wstępnie przyjęto kwadratowy wymiar płyty 180x180x15 w dwóch rzędach.

9.1. Wyznaczenie wartości odporu działającego na płytę .

Uśrednienie ciężaru gruntu, ponieważ miąższości poszczególnych warstw przypadających na wysokość płyty jest taka sama:

γ^(s)=

gdzie:

γ -ciężar objętościowy gruntu;

γ `-ciężar objętościowy gruntu poniżej zwierciadła wody

γ = 18,13 [kN/m³]

γ' = 9,9 [kN/m³]

γ_(s) = 14,015 [kN/m³]

Z_pgr = 0,5·η·γ^(s)·b·H²

gdzie:

b - szerokość boku płyty;

H - zagłębienie płyty;

η - współczynnik zależny od H/h; gdzie h to wysokość płyty.

H/h =2,4/1,8=1,33 > 0,50 płyta nie pracuje jak element ciągły

η = 6,797 /na podstawie interpolacji/

Z_pgr = 493,82 [kN]

9.2. Sprawdzenie czy płyty pracują w grupie.

a = 2·(4·B) =3,36[m]

a_kr = β x b

H/h = 1,33

β = 2,233

a_kr = 4,01

a < a_kr

Warunek spełniony - płyty rozpatrywano jako płyty pracujące w grupie.

9.3. Określenie odległości między rzędami.

Zasięg oblicza się ze wzoru:

R= p·m

gdzie:

m -współczynnik uwzględniający nierównomierne zagęszczenie gruntu; m =1,2

p =

α = 45^o +φ/2

β = 45^o -φ/2

φ = 32,5°

α = 61,25°

β = 28,75°

p = 7 [m]

R = 8,4 [m]

Rozstaw między płytami przyjęto 8,5 [m].

9.4. Wyznaczenie parcia czynnego gruntu.

γ^(n)/γ'	φu^(n)	Ka	Głębokość zi	Zastępcze obciążenie naziomu qz=qn+∑γ·hi	(qz+γi·z)·Ka	2·c^(r)·√Ka	ew	ei	Ea
18,13	32,50	0,30	0,00	10,00	3,01	0,00	0,00	3,01
18,13	32,50	0,30	0,60	10,00	6,28	0,00	0,00	6,28
18,13	32,50	0,30	1,40	10,00	10,65	0,00	0,00	10,65	9,56
9,90	32,50	0,30	0,00	35,38	10,65	0,00	0,00	10,65
9,90	32,50	0,30	1,00	35,38	13,63	0,00	9,81	23,44	17,04
								Ea =	26,60
[kN/m^3]	[^o]	[-]	[m]	[kN/m^2]	[kN/m^2]		[kN/m^2]	[kN/m^2]	[kN/m]

Q_r = R_a·l_s + E_a·b

Q_r = 280,40 [kN]

Q_f = Z_pgr

Q_f = 493,82 [kN]

Q_r < m·Q_f

283,97 < 395,06 [kN]

Warunek spełniony

10.0. Parametry zaprojektowanej ściany szczelnej.

Profile stalowe: Larssen typ V

Ściąg : pręt gładki φ50 mm stal 18G2

Kleszcze: dwa ceowniki C180

Śruby: M20

Płyta kotwiąca: kwadratowa o boku 1,8 m i grubości 15 cm.

1

5

1

19

---