WOJSKOWA AKADEMIA TECHNICZNA
--------------------------------------------------------------------------------------------------------
LABORATORIUM FIZYCZNE
Grupa szkoleniowa E5D9 mgr inż. Andrzej
Wiśniewski
stopień i nazwisko prowadzącego
Monika Majewska
Marcin Pytkowski
( imię i nazwisko słuchacza)
ocena
końcowa ocena przygotowawcza
do ćwiczenia
SPRAWOZDANIE
Z
PRACY LABORATORYJNEJ Nr 20
![]()
Temat: Wyznaczanie z pomiarów efektu magnetronowego.
1. WSTĘP TEORETYCZNY
Jeżeli w jednorodnym polu magnetycznym wstrzelimy prostopadle do linii sił tego pola elektron
(o ładunku = -e) z prędkością ,to na ten ładunek działa siła:
![]()
gdzie:
![]()
-wektory pola elektrycznego i indukcji magnetycznej;
q -dodatni ładunek próbny;
![]()
-wektor prędkości ładunku;
W tym przypadku ![]()
=0,a q = -e, co prowadzi do związku :
![]()
![]()
Wynikiem działania siły na elektron będzie zakrzywienie jego toru w płaszczyźnie prostopadłej do kierunku wektora ![]()
.Ponieważ elektron wciąż porusza się w kierunkach prostopadłych do ![]()
,to kąt stale wynosi /2 i wartość bezwzględna siły Lorentza jest stała ,a więc torem elektronu jest okrąg .Zjawisko to zwie się
efektem magnetronowym .Posłuży ono do wyznaczenia wartości e/m.
Aby tego dokonać należy określić równocześnie trzy wielkości fizyczne :wielkość indukcji magnetycznej, prędkość wstrzelenia elektronu w pole oraz promień okręgu ,po którym on krąży w polu magnetycznym. Trudno jest wyznaczyć przy ustalonym polu magnetycznym krzywiznę toru elektronu ,więc w ćwiczeniu odbędzie się postępowanie odwrotne -- poszukamy pola o takiej indukcji B ,aby elektron krążył z góry wyznaczonym torze (określ. r).
Do tego służy dioda lampowa ,w której cienki drut (katoda) umieszczony jest w osi cylindrycznej anody .Elektrony wychodzące z tejże katody biegną promieniście do anody uzyskując przy tym prędkość
![]()
gdzie Ua jest napięciem przyłożonym między katodę i anodę .
W diodzie lampowej o promieniach anody i katody (odpowiednio ra i rk ;ra <rk)
tor elektronowy zostanie tak zakrzywiony ,aby był on styczny do powierzchni anody, czyli promień musi wynosić:
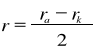
Wartość indukcji w której sytuacja ta nastąpi nazwiemy krytyczną i oznaczymy Bkr
Dioda lampowa umieszczona jest w polu magnetycznym wytwarzanym przez cewkę z prądem .Znając natężenie w polu magnetycznym prądu I płynącego w solenoidzie można wyznaczyć indukcję magnetyczną pola w pobliżu środka cewki za pomocą wzoru :
B = I
Gdzie oznacza empirycznie wyznaczoną stałą .
cel ćwiczenia
Celem ćwiczenia jest wyznaczenie ![]()
z pomiarów efektu magnetronowego.
b) schemat układu pomiarowego
++
Rys. Układ w którym jest badany efekt magnetronowy
W doświadczeniu badana jest zależność prądu anodowego Ia funkcji B przy ustalonym napięciu anodowym.
2.Opis ćwiczenia
2.1 opis
Poszukujemy takiego pola magnetycznego B przy którym elektrony będą krążyć po z góry określonym okręgu. W doświadczeniu badana jest zależność prądu anodowego Ia Przy ustalonym napięciu anodowym.
`
2.2 Dane:
δI = 5 mA błąd pomiaru prądu zasilającego cewkę
δIa = 5 μA błąd pomiaru prądu anodowego
δUa = 0,25 V błąd pomiaru napięcia anodowego
β = 1,35 ⋅ 10-2 T/A empirycznie wyznaczona stała dla cewki
δβ = 0,02 ⋅ 10-2 T/A błąd wyznaczenia stałej
ra = 0,8 mm promień anody
δra = 0,01 mm błąd promienia anody
rk = 0,05 mm promień katody
δrk = 0,01 mm błąd promienia katody
2. OPRACOWANIE WYNIKÓW POMIARU
I [mA] |
dla Ua=6 [V] |
dla Ua=8 [V] |
dla Ua =10 [V] |
|
|
Ia [μA] |
|
0 |
25,8 |
39,1 |
51,1 |
20 |
26 |
39,5 |
51,9 |
40 |
26,1 |
39,9 |
52,1 |
60 |
26 |
39,1 |
51,8 |
80 |
26,1 |
39,0 |
51,5 |
100 |
25 |
38,9 |
51,2 |
110 |
24,5 |
38,8 |
51,1 |
120 |
24,2 |
38,5 |
51 |
130 |
23,9 |
36,5 |
49,1 |
140 |
23,3 |
36,2 |
49 |
150 |
22 |
35,7 |
48,5 |
160 |
20,9 |
32,5 |
47,9 |
170 |
19 |
20,9 |
45,3 |
180 |
13 |
20,6 |
38,5 |
190 |
12 |
20,9 |
36 |
200 |
11,5 |
18,2 |
28 |
220 |
9 |
16,1 |
22 |
240 |
8,2 |
13,9 |
19 |
260 |
7,1 |
11,8 |
17,9 |
280 |
6,5 |
10,2 |
15,1 |
300 |
5,7 |
9,8 |
14,1 |
320 |
5,1 |
9,1 |
13,2 |
340 |
4,9 |
7,9 |
11,5 |
360 |
4,5 |
7,5 |
10,9 |
380 |
4,1 |
7,2 |
10,2 |
400 |
4 |
6,9 |
9,5 |
4. Wykresy (w załączeniu)
5. Zestawienie wyników
Ua [V] |
Ikr [A] |
Bkr [T] |
e/m [C/kg] |
(e/m)śr [C/kg] |
Błąd bezwzgl. (e/m)gr [C/kg] |
Błąd wzgl. (e/m) |
6 |
0,178 |
0,00240 |
1,48⋅1011 |
1,73⋅1011 |
6,32⋅109 |
0,04 |
8 |
0,184 |
0,00248 |
1,84⋅1011 |
|
4,35⋅109 |
0,02 |
10 |
0,203 |
0,00274 |
1,89⋅1011 |
|
5,09⋅109 |
0,02 |
6. Obliczenia
6.1 Obliczenie indukcji magnetycznej w pobliżu środka cewki Bkr
Korzystamy ze wzoru:
Bkr = β ⋅ Ikr
Bkr1 =1,35 ⋅ 10-2 T/A ⋅ 0,178 A = 0,240⋅ 10-2 T
Bkr2 =1,35 ⋅ 10-2 T/A ⋅ 0,184 A = 0,248⋅ 10-2 T
Bkr3 =1,35 ⋅ 10-2 T/A ⋅ 0,203 A = 0,274⋅ 10-2 T
6.2 Obliczanie e/m
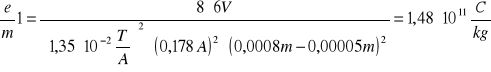
![]()
Korzystamy z wzoru:
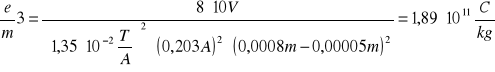
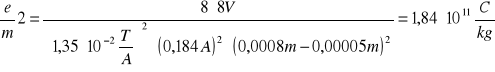
6.3 Obliczanie średniej arytmetycznej e/m
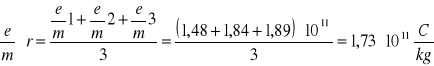
6.4 Obliczanie błędów:

6.4.1 Obliczanie błędów bezwzględnych granicznych dla poszczególnych pomiarów
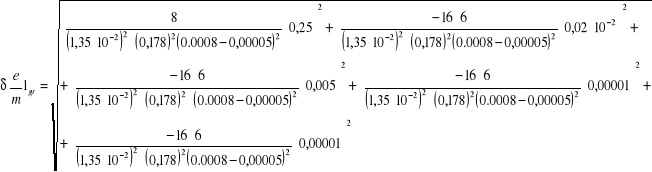
![]()
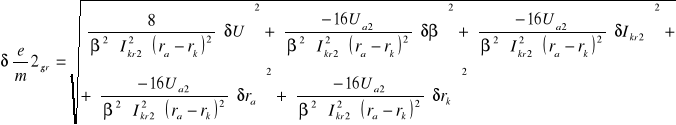
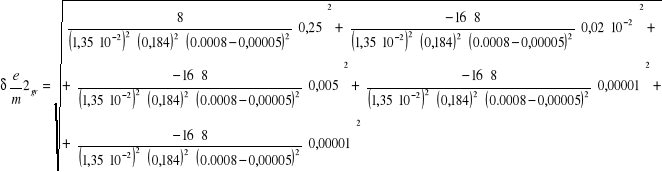
![]()
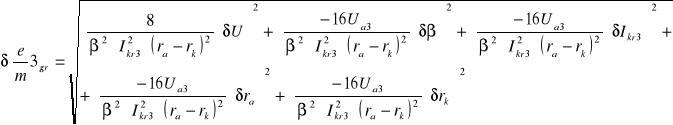
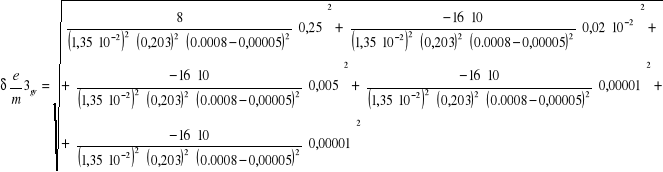
![]()
6.4.2 Obliczanie błędów względnych dla poszczególnych pomiarów
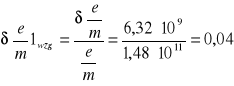

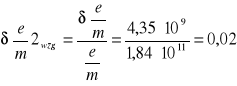
Średni błąd względny
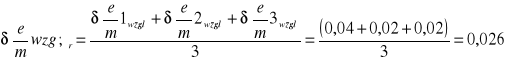
3. Wnioski
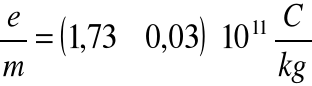
Wartość ładunku właściwego wyznaczona przez nas wynosi:
Otrzymany przez nas wynik niewiele odbiega od wartości teoretycznej, która wynosi 1,75⋅1011 C/kg.
Na błąd wpłynęła graficzna metoda wyznaczenia prądu krytycznego Ikr ,ale nasz wynik i obliczony błąd zawiera w sobie wartość teoretyczną ładunku właściwego, tak że cel został osiągnięty. Ćwiczenie wykonaliśmy z dużą dokładnością, o czym świadczy niewielki błąd względny, który wynosi 2,6 %.
LITERATURA
S. Bartnicki, W. Borys T. Kostrzyński: Fizyka ogólna, ćwiczenia laboratoryjne, cz. I, WAT Warszawa 1994
![]()
![]()
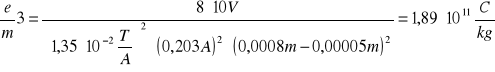
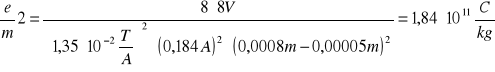
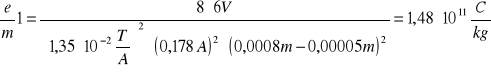
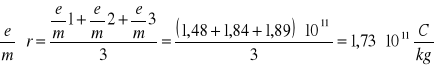
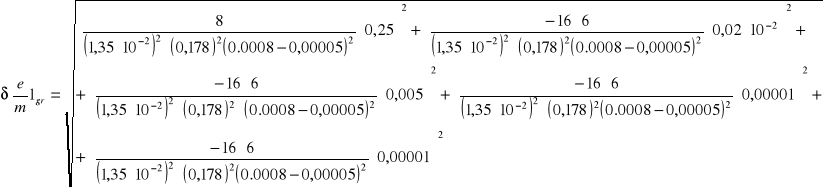
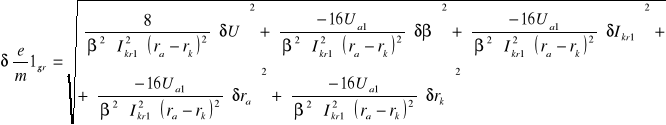
![]()
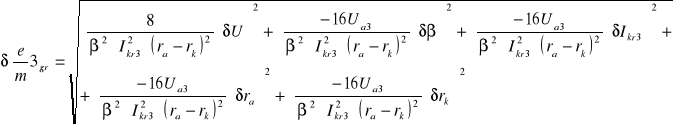
![]()
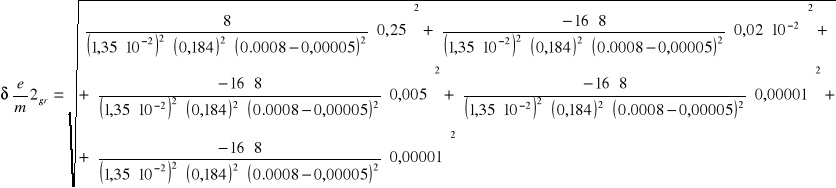
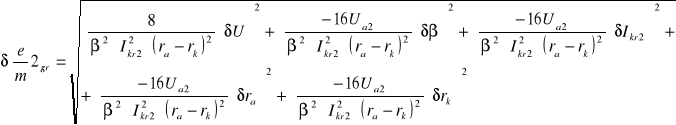
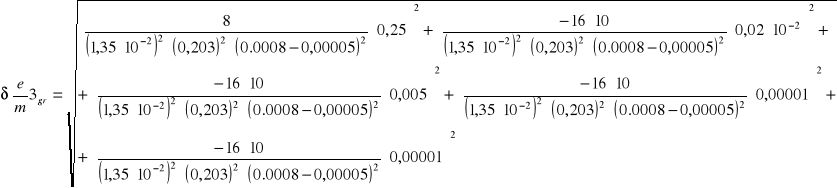
![]()
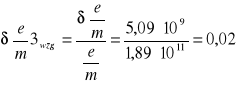
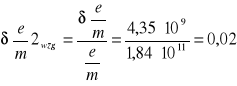
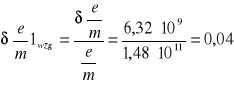
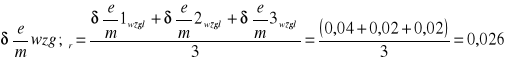
![]()
Wyszukiwarka
Podobne podstrony:
cw 20 Instrukcja
fin przeds ćw 20 11
cw 20 protokol
cw.20
cw 20 formularz
instrukcja cw 20 id 216489 Nieznany
Ćw. 20, chemia fizyczna, Nowy folder
Cw 20 - Wyznaczanie stosunku cp-cv dla powietrza metoda Clementa-Desormesa, Studia, Budownictwo UTP,
Ćw 1 20.02.2008, studia, Kardiologia
Cw. 4 20. 02.2012, Biologia, zoologia
ćw.20, Fizyka, Skrypt do Laborek
PODSTAWY ZARZĄDZANIA ćw 20.03.10 20, Materiały studia, Podstawy zarządzania ćwiczenia
Technologia ścieków ćw 20 Oznaczanie zdolności natleniania OC
Ćw 2 20.03.2008, studia, Dermatologia
Ćw 6 20.03.2008, studia, Kinezyterapia, Ćwiczenia
cw 20
Ćw 20 szablon
CW 20, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania), Cw 20
ĆW 20
więcej podobnych podstron