Controlling prospektywny w niewielkim przedsiębiorstwie handlowym

1.1. Cechy przedsiębiorstwa

Przedsiębiorstwo handlowe, spółka prawa handlowego, sprzedaje tylko jeden rodzaj towaru. Na popyt oddziałuje aktywnie tylko ceną sprzedaży. Innymi instrumentami oddziaływania na popyt posługuje się w niewielkim stopniu, stabilnie, niezależnie od polityki cenowej. W tej sytuacji intensywność sprzedaży zmienia się tylko w zależności od ceny. Na rynku nie występują substytuty sprzedawanego produktu. Przedsiębiorstwo posiada stałych odbiorców, zna więc doskonale rynek. Proces sprzedaży jest ustabilizowany. W jednakowych odstępach czasu, przy określonej cenie, sprzedaje takie same w przybliżeniu ilości towaru. Przedsiębiorstwo działając w warunkach pewności kupuje dokładnie tyle samo towaru, ile wynosi popyt, zatem ilość sprzedanych jednostek towaru jest równa popytowi. Sprzedaż odbywa się z kredytem kupieckim, przy czym okres kredytowania jest na stałe określony. Zatrudnienie w owej małej firmie wynosi kilka osób na stałe zatrudnionych oraz grupę osób; zmienną - w zależności od intensywności prowadzonej działalności.

Przedsiębiorstwo jest zdolne do identyfikowania modelu popytu jako funkcji ceny. Przepływy finansowe na rachunku bieżącym kształtują się stabilnie, powtarzalnie. Kapitał obrotowy przedsiębiorstwo w całości pokrywa kredytem obrotowym o ustalonej stopie procentowej. Stany zobowiązań i należności zależą od czasu, na jaki są udzielane kredyty kupieckie; odpowiednio przy zakupach towaru oraz jego sprzedaży. Decyzji operacyjnych przedsiębiorstwa nie ograniczają sztywno ustalenia strategiczne. Dąży ono w swojej działalności do maksymalizacji wyniku finansowego.

Przyjęte ustalenia wskazują, że przedsiębiorstwo działa w wygodnych dla siebie, zbliżonych do deterministycznych warunkach.

1.2. Model przedsiębiorstwa

Jak ustalono wcześniej, mianem modelu przedsiębiorstwa będziemy nazywać zespół funkcji wyrażających zależności pomiędzy istotnymi wielkościami charakteryzującymi stan przedsiębiorstwa. W celu jego utworzenia na początek określimy wielkości, przy użyciu których będziemy charakteryzować ów stan i sporządzimy graf interakcji wyrażający poglądowo zachodzące między nimi zależności. Ukazuje go rysunek (Rys. 1.1). Węzłami grafu są wyróżnione wielkości. Gałęzie grafu określają bezpośrednie zależności zachodzące pomiędzy parami wielkości. Jest to graf skierowany. Strzałki na krawędziach grafu sygnalizują zwrot zachodzących między węzłami grafu zależności przyczynowo-skutkowych. Gdy wielkość wyrażona węzłem będącym następnikiem w danej parze wielkości zależy pozytywnie od wielkości, którą wyraża węzeł poprzednik, opatrujemy daną krawędź grafu znakiem „plus”. W przeciwnym przypadku zaznaczymy „minus”. Dla orientacji wprowadzamy symbole poszczególnych wielkości stanowiących węzły grafu, aby móc dalej do nich się odnosić przy ich matematycznym definiowaniu.

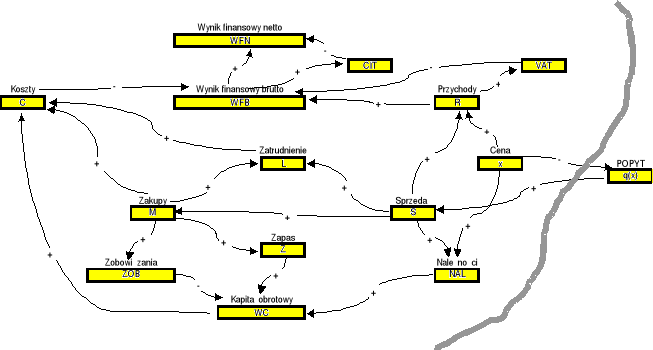
Rys. 1.1: Graf interakcji wielkości charakteryzujących stan przedsiębiorstwa

Omówmy bliżej proces konstruowania grafu interakcji. Budowanie grafu najlepiej rozpocząć od wielkości, która stanowić będzie główny cel przedsiębiorstwa w obranym odpowiednio krótkim dystansie czasowym T. W danym przypadku ograniczamy się do jednego celu zasadniczego. Będzie nim wynik finansowy netto WFN, który stanie się dalej głównym kryterium oceny poszczególnych wersji planu operacyjnego. Wynik finansowy netto zależy bezpośrednio od wyniku finansowego brutto WFB i wielkości podatku dochodowego CIT, który przedsiębiorstwo odprowadzi od uzyskanego wyniku finansowego brutto (jeżeli okaże się on dodatni). Stwierdzimy następnie, że wynik finansowy brutto zależy bezpośrednio od przychodów R i kosztów C oraz pozostającego do zapłacenia podatku VAT. Przychody będą zależeć bezpośrednio od ilości sprzedanego towaru S i jego ceny x. Sprzedana ilość towaru będzie określona przez popyt q(x), a ten w rozpatrywanym przypadku będzie określać tylko cena. Okres odroczenia terminu płatności za zrealizowane dostawy towaru, cena x oraz ilość sprzedanego towaru S, będą określać skalę należności NAL. Z kolei stan zobowiązań ZOB będzie określać skala dokonywanych zakupów towaru M, z uwzględnieniem stosowanego przez dostawcę okresu odroczenia płatności. Wielkość kapitału obrotowego przedsiębiorstwa WC będzie uzależniona (głównie) od stanu należności, zobowiązań oraz wartości zapasów towaru. W grafie uwzględniamy jeszcze poziom zatrudnienia L, który - w podstawowej kategorii pracowników - będzie proporcjonalny do skali sprzedaży. Koszty w danym przypadku będą przede wszystkim zależeć od skali zakupów towaru; także od wielkości zatrudnienia oraz kapitału obrotowego (koszty finansowe). Powiększają je oczywiście koszty stałe przedsiębiorstwa. Większość wielkości reprezentowanych przez węzły grafu zależy oczywiście równocześnie od licznych parametrów, których w ogólnym modelu nie ma potrzeby wyróżniać.

Spójrzmy teraz na graf i ustalmy, które węzły reprezentują w nim wielkości podlegające decyzjom operacyjnym. Przeanalizujmy w tym celu istotę poszczególnych węzłów grafu interakcji. Nie podlega oczywiście decyzjom skala przychodów i kosztów, a tym bardziej wynik finansowy. Są one funkcjami pozostałych wielkości reprezentowanych przez węzły grafu. Przedsiębiorstwo nie decyduje wprost o skali sprzedaży. Orientując się na rynek dostosowuje po prostu skalę realizowanej sprzedaży do popytu. Wielkość sprzedaży nie jest więc przedmiotem decyzji. Przedsiębiorstwo, wykorzystując możliwość identyfikacji modelu popytu, tak kształtuje popyt, a w konsekwencji sprzedaż, aby maksymalizować wynik finansowy netto. Stwierdzono już wcześniej, że przedsiębiorstwo oddziałuje aktywnie na popyt jedynie ceną. Cena sprzedaży jest więc niewątpliwie wielkością decyzyjną. Sprzedaż wyznacza strumień zakupów towaru, które tym samym także nie są przedmiotem decyzji. Należności, przy stałym okresie odroczenia terminu płatności, są funkcją strumienia sprzedaży i ceny sprzedaży. W żadnej mierze nie podlegają więc bieżącym decyzjom. Podobnie zobowiązania z tytułu dokonywanych zakupów towaru są funkcją strumienia zakupów, przy określonym przez dostawcę okresie odroczenia płatności za dostawy. Przedsiębiorstwo, zawierając umowę z dostawcą powinno określić jak częste i jak duże będą dostawy. Powinno w tym celu przygotować się do negocjacji z dostawcą, wyznaczając najkorzystniejszą dla siebie wielkość partii dostaw u. Sprowadza bowiem towar partiami. Jest więc istotne jak duże będą to partie, a w konsekwencji jak często pojawiać się będą dostawy i jaki w konsekwencji będzie średni zapas Z towaru utrzymywany w przedsiębiorstwie. Od tego zależą zmienne koszty magazynowania i koszty odnawiania zapasu. Skala kapitału obrotowego przedsiębiorstwa będzie wyznaczona przez należności, wartość średniego zapasu towaru i zobowiązania. Nie podlega więc decyzji. Zatrudnienie w części zależnej od skali prowadzonej działalności zmienia się wraz z nią. Wyznacza je automatycznie wielkość sprzedaży. Można więc przyjąć, że skala zatrudnienia nie jest przedmiotem decyzji operacyjnej.

W rezultacie możemy skonstatować, że przedsiębiorstwo w swoim działaniu ma do czynienia z dwiema zmiennymi decyzyjnymi. Są nimi

• cena sprzedaży x,

• wielkość partii dostawy towaru u.

Decyzje dotyczące ceny i wielkości partii dostawy towaru warunkują się nawzajem, jak wszystkie decyzje operacyjne. Wielkość partii dostawy kształtuje pośrednio niejako normatywny średni poziom zapasu towaru. Zmiana zapasu towaru zmienia poziom kapitału obrotowego przedsiębiorstwa, a w konsekwencji koszty finansowe i koszty ogółem. W następstwie zmienia się więc wynik finansowy, który - zgodnie z przyjętym założeniem - jest głównym kryterium decyzyjnym, a w danym przypadku zarazem będzie pełnił wprost rolę kryterium decyzji cenowej. Zmiany kosztów wymagają dostosowania poziomu ceny sprzedaży. Ta przekłada się na wielkość sprzedaży, co zazwyczaj będzie powodować potrzebę zmiany - jeżeli to możliwe - wielkości partii dostaw. Koło się zamyka. Kolejna zmiana średniego zapasu towaru spowoduje ponownie pewną zmianę kosztów. W konsekwencji zmieniać się będą pozostałe wielkości wyróżnione w grafie interakcji. Określona w cenach zaopatrzeniowych wartość średniego zapasu towaru wpływa bowiem na wielkość kapitału obrotowego, a zatem na koszty finansowe. Zmiana kosztów odbija się oczywiście znowu na wyniku finansowym, co wymaga skorygowania ceny. Jeżeli jednak postępowanie decyzyjne jest prowadzone prawidłowo, następujące zmiany obrazu stanu przedsiębiorstwa będą w wyniku kolejnych następujących po sobie operacji decyzyjnych coraz mniej znaczące. Skonstatujmy więc jeszcze raz: decyzje, poprzez które dokonuje się sterowanie przedsiębiorstwem są współzależne i nie powinny być podejmowane w oderwaniu od siebie. Okaże się zresztą dalej, iż będziemy w stanie wyprowadzić wzór na optymalną wielkość partii dostawy towaru, który pozwoli na automatyczne dostosowywanie wielkości partii dostawy do strumienia sprzedaży. W rezultacie zmienna u będzie funkcją zmiennej x.

Przedsiębiorstwo powinno tak kształtować podlegające decyzjom operacyjnym wielkości, aby osiągany w efekcie prowadzonej działalności wynik finansowy netto w przyjętym okresie, oznaczanym dalej symbolem T, stanowiącym czasowy horyzont planowania, był maksymalny. Wynik finansowy netto zależy od wymienionych wyżej zmiennych decyzyjnych. Rozpatrywane przedsiębiorstwo jest sterowane za pośrednictwem planu operacyjnego obejmującego równocześnie cenę sprzedaży i normę zapasu towaru. Wielkości mające charakter zmiennych decyzyjnych mogą być określane arbitralnie (przy zastosowaniu postępowania symulacyjnego), albo optymalizacyjnie.

Przystąpmy do systematycznego opisu formalnego wielkości potraktowanych jako węzły grafu przedstawionego na rysunku (Rys. 1.1), przedstawiając funkcje określające wielkości niedecyzyjne.

• Wynik finansowy netto WFN

(1.1)

gdzie

WFB - wynik finansowy brutto,

CIT - kwota podatku dochodowego.

• Podatek dochodowy CIT

, (1.2)

przy czym

,

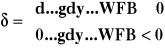
gdzie

d  stopa podatku dochodowego.

Podatek dochodowy (CIT) jest naliczany w przypadku, gdy wynik finansowy brutto podatnika jest dodatni. Zatem użyta tu zmienna logiczna δ jest definiowana na poziomie ustawowej stawki podatku dochodowego jedynie wtedy, gdy wynik finansowy brutto jest większy od zera. W przeciwnym przypadku musi przyjmować wartość zero.

• Wynik finansowy brutto WFB

Wynik finansowy brutto potraktujemy jako różnicę przychodów i kosztów z uwzględnieniem podatku VAT.

, (1.3)

gdzie

R - kwota przychodów finansowych przedsiębiorstwa,

C - kwota kosztów przedsiębiorstwa,

VAT - kwota podatku VAT do zapłacenia.

• Przychody R

, (1.4)

gdzie

x - cena sprzedaży za jednostkę towaru,

S - wielkość sprzedaży (liczba sprzedanych w okresie T jednostek towaru).

Przychody firmy pochodzą ze sprzedaży jej jedynego towaru. Pomijamy dla uproszczenia ewentualne wpływy z innych źródeł, mające charakter marginesowy i incydentalny.

• Podatek od wartości dodanej VAT

, (1.5)

gdzie

v - stopa podatku VAT,

MC - wartość dokonywanych zakupów, w tym w szczególności zakupów towaru.

Funkcja (1.5) wyznacza poziom pozostającego do zapłacenia podatku VAT. Jej postać wynika z takiego oto rozumowania. Ceny sprzedaży towarów są określane przez sprzedających. Obejmują one podatek VAT. Jeżeli jednak nabywcy nie są płatnikami VAT (np. nabywcy detaliczni), nie interesuje ich jaką część ceny stanowi obciążenie podatkowe sprzedającego. Reagują po prostu na podyktowaną cenę sprzedaży danego dobra. Płatnicy VAT natomiast interesują się skalą podatku VAT tkwiącą w koszcie nabywanego towaru, ponieważ mogą ją odliczać od przypadających na nich należnych kwot tego podatku. Nie można jednak już dziś mówić, że cena sprzedaży powstaje poprzez doliczenie do pewnej ceny bazowej obliczonego narzutu związanego z podatkiem VAT. Ceny są określane w następstwie negocjacji z nabywcami, względnie po prostu na mocy arbitralnych decyzji dostosowywanych do cen występujących na rynku substytutów. Coraz częściej u podstaw określania cen leży także przynajmniej proste postępowanie optymalizacyjne. Przed rozwiązaniem problemów decyzyjnych nie wiadomo więc jaką będzie bezwzględna kwota obciążenia VAT-owskiego stanowiąca odpowiednio część dyktowanej przez sprzedającego ceny sprzedaży. Trzeba ją obliczać na podstawie ceny sprzedaży x.

Mechanizm podatku VAT zakłada, że cena sprzedaży (brutto) powstaje w wyniku powiększenia ceny netto o kwotę podatku wynikającą z obowiązującej stopy podatkowej, mianowicie

, (1.6)

gdzie

xⁿ - cena netto (bez narzutu podatku VAT).

Jednak, jak wyżej stwierdzono, cena netto xⁿ nie jest z góry znana. Znana jest za to cena sprzedaży x. Cena netto xⁿ jest funkcją sprzedaży ceny x. Mianowicie

. (1.7)

Zatem wartość sprzedaży netto Rⁿ (wartość sprzedaży brutto pomniejszona o należny podatek VAT) wynosi

. (1.8)

Kwotę należnego podatku od wartości dodanej VAT^nal można więc wyznaczyć jako różnicę przychodów brutto R i przychodów netto Rⁿ, a mianowicie

(1.9)

Przedsiębiorstwo nie zapłaci jednak w całości tej kwoty, gdyż - jak wiadomo - mechanizm podatku VAT przewiduje odliczenie podatku wcześniej zapłaconego w cenach nabywanego towaru, jak również i innych dóbr. Potrzebne jest więc uwzględnienie kwoty podatku VAT^odl podlegającej odliczeniu. Przyjmując w danym przypadku, że zakupy towarowe i wszystkie inne obłożone są podatkiem VAT o jednakowej stopie v, możemy zapisać

. (1.10)

Zatem kwotę podatku VAT pozostającą do zapłacenia możemy wyznaczyć jako różnicę kwoty podatku należnego i wcześniej zapłaconego, co prowadzi do formuły wyrażonej wzorem (1.5).

• Sprzedaż S

Skoro istnieje możliwość wyznaczenia popytu przy cenie sprzedaży x i skoro tym samym wielkość popytu jest określona deterministycznie, byłoby nielogiczne dopuszczać poziom sprzedaży mniejszy od popytu kierującego się ku towarowi oferowanemu przez przedsiębiorstwo. Sprzedaż mniejsza od popytu oznaczała by poważny błąd popełniony w procesie zarządzania. Przedsiębiorstwo powinno tak określić cenę sprzedaży, a w konsekwencji popyt, aby zrealizowana sprzedaż maksymalizowała osiągnięty wynik finansowy. Logiczne będzie zatem przyjąć, że wielkość sprzedaży powinna być równa popytowi, czyli

, (1.11)

gdzie

q(x) - popyt na towar, jako funkcja ceny x.

Tym samym poziom sprzedaży towaru jest funkcją ceny, po jakiej sprzedawany jest towar.

• Popyt q(x)

W miarę wzrostu ceny x popyt q(x) maleje. Można wykazać, że kształtowanie się popytu w zależności od ceny odpowiada funkcji logistycznej o przebiegu malejącym w miarę wzrostu wartości argumentu funkcji. Można zatem zapisać

, (1.12)

gdzie

*, *, *- parametry logistycznej funkcji popytu; przy czym *,*,*>0.

• Należności NAL

Przedsiębiorstwo udziela kredytu kupieckiego swoim klientom. W konsekwencji powstają należności, których poziom zależy od przesunięcia terminu płatności w stosunku do momentów dostarczenia towaru.

, (1.13)

gdzie

* - okres odroczenia terminu płatności stosowany względem nabywców towaru.

• Ilość kupowanego towaru M

Jest naturalne, iż przedsiębiorstwo zdolne do precyzyjnego planowania swoich działań będzie dokonywać partiami zakupów towaru w łącznej ilości dokładnie odpowiadającej skali sprzedaży w okresie T. Zatem

. (1.14)

• Zobowiązania ZOB

Analogicznie do zasady udzielania kredytu kupieckiego przy sprzedaży towaru przedsiębiorstwo korzysta z kredytu kupieckiego przy dokonywaniu zakupów. Poziom zobowiązań będzie zależał od okresu odraczania przez dostawcę terminu płatności oraz oczywiście od ich skali. Prowadzi to do funkcji

, (1.15)

gdzie

 - okres odroczenia terminu płatności za realizowane przez dostawcę dostawy towaru.

• Kapitał obrotowy WC

Kapitał obrotowy określimy jako sumę należności i wartości zapasu towaru, pomniejszoną o poziom zobowiązań. Zatem

, (1.16)

gdzie

p - cena zaopatrzeniowa towaru,

Z - wielkość normy zapasu towaru,

RB - norma środków finansowych na rachunku bieżącym firmy.

• Zatrudnienie pracowników fizycznych L w zależności od skali prowadzonej działalności

Przedsiębiorstwo ma orientację co do ilości pracowników wykonujących zadania bezpośrednie potrzebnych dla wykonania pracy podstawowej w wymiarze jednostkowym. Zgodnie z wcześniejszym ustaleniem ilość ta jest wprost proporcjonalna do skali sprzedaży. Oznacza to, iż przedsiębiorstwo reguluje płynnie zatrudnienie w kategorii pracowników fizycznych stosownie do doraźnych potrzeb. Prowadzi to do zapisu

, (1.17)

gdzie

l^fiz - wskaźnik zatrudnienia pracowników bezpośrednich odpowiadający jednostce sprzedawanego towaru.

• Koszty C

Funkcja kosztów jest złożeniem elementarnych funkcji określających poszczególne składowe kosztów.

, (1.18)

gdzie

MC - koszty zaopatrzeniowe,

PC - koszty osobowe,

FC - koszty finansowe,

C⁰ - koszty stałe firmy w czasie T.

W dalszym ciągu zdefiniujemy poszczególne składniki kosztów rozwijając z osobna określające je funkcje.

• koszty zaopatrzeniowe

, (1.19)

gdzie

k^od - koszt związany z jednorazowym odnowieniem zapasu towaru,

n - liczba partii dostaw w okresie T,

MC^inne - wartość innych niż towar zakupów materiałowych;

• koszty osobowe

, (1.20)

gdzie

w₁ - średnie wynagrodzenie brutto pracownika zatrudnionego na stałe,

w₂ - średnie wynagrodzenie brutto pracownika fizycznego, zatrudnionego na poziomie podstawowym, w zależności od skali sprzedaży,

L₀ - liczba zatrudnionych na stałe.

• koszty finansowe

, (1.21)

gdzie

c - stopa kredytowa.

W ten sposób został zakończony matematyczny opis współzależnych wielkości tworzących charakterystykę stanu przedsiębiorstwa. Nie objął on jednak wielkości zakwalifikowanych jako decyzyjne. Przedstawione formuły odpowiadają wyróżnionym wielkościom reprezentowanym przez węzły grafu interakcji. Cały ich zespół tworzy model matematyczny, który posłuży dalej jako podstawowe narzędzie w procesie controllingu prospektywnego. Dla określania wielkości decyzyjnych, a więc ceny sprzedaży x oraz normatywnego średniego poziomu zapasu towaru u, przewidziano procedury oparte na modelach optymalizacyjnych przedstawionych w dalszym ciągu.

1.3. Modele optymalizacyjne

1.3.1. Problem ceny sprzedaży

Kluczowym problemem decyzyjnym w każdym przedsiębiorstwie jest problem strategii rynkowej. W danym przypadku strategią rynkową będzie po prostu cena sprzedaży towaru. Inne nieobojętne dla kształtowania się popytu wielkości - np. stosowany okres odroczenia terminu płatności za zrealizowane dostawy towaru do odbiorców - są tu wielkościami stałymi, a więc parametrami. Operując programowaniem nieliniowym można znaleźć taki poziom ceny WFN(x), który będzie maksymalizował wynik finansowy netto. Istnieje przy tym możliwość uwzględnienia dowolnych warunków ograniczających i brzegowych. Ideę owej optymalizacji można wyrazić zapisując ogólną postać funkcji wyniku finansowego netto, jako funkcji celu prowadzonej optymalizacji, mianowicie

, (1.22)

przy czym

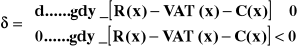
gdzie

WFN(x) - wynik finansowy netto potraktowany jako funkcja ceny sprzedaży towaru,

R(x) - przychody brutto potraktowane jako funkcja ceny sprzedaży towaru,

VAT(x) - kwota podatku VAT do zapłaty, jako funkcja ceny sprzedaży towaru,

C(x) - koszty ogółem będące funkcją ceny sprzedaży towaru,

d - stopa podatku dochodowego.

Postaci elementów funkcji wyniku finansowego netto, mianowicie funkcji przychodów R, kosztów C i wielkości podatku VAT podano wcześniej.

Funkcja (1.22) zostanie dalej wykorzystana jako model optymalizujący strategię rynkową firmy, którą to strategią w danym przypadku jest po prostu cena sprzedaży towaru x. Nie zostały określone żadne zastrzeżenia krępujące swobodę decyzyjną w tym zakresie. Zatem w modelu optymalizacyjnym nie uwzględniono żadnych warunków ograniczających.

Należy podkreślić, że w zasadzie nie istnieje możliwość rozwiązania w sposób analityczny tak sformułowanego problemu, mimo prostoty konstrukcji wyrażającego go modelu. Funkcja (1.22) posiada bowiem nieciągły charakter powodowany przez mechanizm podatku dochodowego. Można byłoby co najwyżej poszukiwać jej maksimum odpowiednio określając osobno pochodne w przedziałach wartości ujemnych i dodatnich wartości funkcji. Jednak i w tym przypadku próba znalezienia rozwiązania parametrycznego w klasyczny sposób skończy się najczęściej niepowodzeniem, ponieważ trzeba byłoby rozwiązywać równanie funkcji uwikłanych lub układy takich funkcji. Zauważmy przy tej okazji, że rozwiązywalne w oparciu o analizę matematyczną są tylko modele oparte na funkcjach najprostszych, wręcz elementarnych. Klasyczne podejście do rozwiązywania zagadnień optymalizacyjnych nie jest więc godne polecenia na użytek praktyki zarządzania. Na szczęście dysponujemy dziś techniką obliczeniową, która pozwala znajdować optymalne rozwiązania problemów decyzyjnych w sposób numeryczny, bez potrzeby uciekania się do analizy matematycznej.

1.3.2. Problem wielkości partii dostawy towaru

Należy zauważyć, iż wynik optymalizacji ceny będzie zależny między innymi od decyzji dotyczącej skali normy zapasu towaru, która jest związana z wielkością partii dostawy. Od wielkości partii dostawy towaru zależy bowiem średni zapas towaru, zatem i poziom kapitału obrotowego, który generuje koszty finansowe. W konsekwencji wielkość partii dostawy ma wpływ na koszty, a więc i na wynik finansowy, który jest kryterium decyzji cenowej. Warto więc, by i ta decyzja była wspomagana optymalizacyjnie. Przy przyjętej charakterystyce uwarunkowań działania firmy usprawiedliwione jest zastosowanie w tym celu metody deterministycznej. Można tu użyć klasycznej metody prowadzącej do określania wielkości partii dostaw towaru przy kryterium minimalizacji sumy zmiennych kosztów magazynowania i kosztów związanych z przyjmowaniem dostaw i jako normę zapasu potraktować połowę tej wielkości. Jednak klasyczne podejście do tego zagadnienia ignoruje fakt operowania przez dostawcę kredytem kupieckim, przy określonym terminie płatności za zrealizowane dostawy. Kwestia ta wymaga wyjaśnienia.

Klasyczna metoda określania optymalnej wielkości partii dostawy towaru jest oparta na założeniu - nie artykułowanym na ogół w literaturze - że płatność za dostawę dokonywana jest gotówkowo. Wówczas zmienne koszty finansowe wynikające z zamrożenia kapitału w zgromadzonym zapasie obciążają w całości gromadzącą zapas firmę. Tymczasem to właśnie koszty wynikające z zamrożenia kapitału w zapasie stanowią lwią część zmiennych kosztów magazynowania przypadających na jednostkę zapasu w okresie jednostkowym. Jeśli zatem dostawca stosuje kredyt kupiecki, przejmuje niejako na siebie koszt finansowy wynikający z zamrożenia kapitału w okresie kredytowania. Odpowiednio niższy jest więc ponoszony przez odbiorcę zmienny koszt magazynowania. Należy dobitnie podkreślić, że koszty stałe magazynowania, np. stałe koszty wynagrodzeń czy amortyzacji, nie mają wpływu na optymalną wielkość partii dostawy.

W danym przypadku należy przyjąć, iż strumień sprzedaży jest taki sam w kolejnych dniach, a więc jest określony deterministycznie, ponieważ stwierdzono na wstępie, że prowadzona przez firmę sprzedaż ma charakter ustabilizowany, stały w kolejnych jednostkach czasu. Z tego samego powodu można deterministycznie określić wielkość zapotrzebowania na towar w czasie T. Wielkość zapotrzebowania na towar w czasie T oznaczymy symbolem M. Znane i stałe są zarazem jednostkowe zmienne koszty magazynowania k^mag oraz koszty odnowienia zapasu k^od. Okres kredytowania kupieckiego przez dostawcę wynosi . Przyjmijmy, że jednostką czasu jest doba.

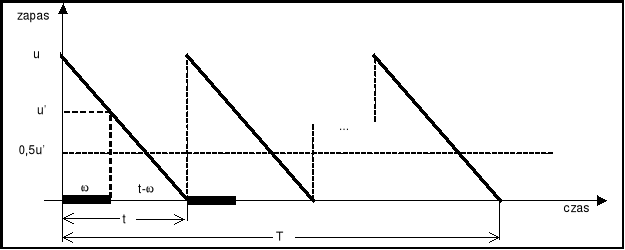
Przebieg kształtowania się zapasów w czasie można zilustrować rysunkiem (Rys. 1.2).

Rys. 1.2: Kształtowanie się zapasu towaru w czasie

Na rysunku poszukiwaną wielkość partii dostawy oznaczono symbolem u. Jest to zmienna decyzyjna. Pogrubione ukośne linie symbolizują kształtowanie się zapasu w czasie. Są to odcinki linii prostych ze względu na założenie, że proces poboru zasobu towaru odbywa się jednostajnie, proporcjonalnie do czasu. Poziom zapasu waha się pomiędzy wielkością dostawy u i zerem. Dostawy z założenia muszą być tak zsynchronizowane, aby w momencie zbliżenia się poziomu zapasu do zera pojawiała się w magazynie kolejna dostawa i następowało „odnowienie” zapasu do poziomu u. Czas trwania jednego cyklu dostaw oznaczono symbolem t. Część tego odcinka czasu jest pokryta czasem trwania kredytu kupieckiego  zapewnianego przez dostawcę. W czasie , jak już stwierdzono, firma odbierająca towar nie ponosi zmiennych kosztów magazynowania, którymi są koszty wynikające z zamrożenia kapitału. Zatem w każdym odcinku czasu t rozważana firma ponosi koszt magazynowania tylko w przedziale czasu t-. W tym przedziale czasu zapas zmienia się od poziomu u' do zera. Zatem średnio zapas generujący zmienne koszty magazynowania wynosi połowę wielkości u', czyli 0,5u'. Łatwo zarazem zauważyć, że okres planowania T składa się z pewnej liczby odcinków czasu, jaki upływa między kolejnymi dostawami. Czas upływający od jednej dostawy do następnej oznaczono symbolem t. Liczbę takich cykli oznaczymy symbolem n.

Rozwiążemy dalej ten prosty problem w sposób parametryczny, wyprowadzając wzór na optymalną wielkość partii u*.

Jest niezbędne wyznaczenie wielkości n, t i u'. Jeżeli wielkość jednej dostawy ma wynosić u, to liczba dostaw będzie równa ilorazowi ogólnego zapotrzebowania na towar Q i wielkości jednej partii dostawy, czyli

. (1.23)

Z kolei czas trwania jednego cyklu dostaw wyniesie

. (1.24)

Wielkość u' można wyznaczyć z proporcji

,

skąd

. (1.25)

W konsekwencji sumę zmiennych kosztów magazynowania można określić jako

, (1.26)

skąd

. (1.27)

Sumę łącznych kosztów odnawiania zapasu wyrazi zapis

. (1.28)

W rezultacie funkcja łącznych zmiennych kosztów magazynowania i kosztów odnawiania zapasu przybierze postać

. (1.29)

Jest to funkcja jednej zmiennej u. Na jej podstawie można określić taką wartość wielkości partii dostawy u, która minimalizuje funkcję K.

Funkcja ta jest różniczkowalna. Można zatem znaleźć jej minimum w oparciu o klasyczną technikę analizy matematycznej w sposób parametryczny. Pierwsza pochodna funkcji K posiada postać

, (1.30)

skąd po przyrównaniu do zera i rozwiązaniu tak powstałego równania otrzymamy wzór na optymalną wielkość partii dostawy towaru u* minimalizującą wartość funkcji K.

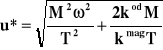
. (1.31)

Warto zauważyć, że w przypadku gdy płatności za dostawy odbywają się gotówkowo (=0), wzór przybiera postać

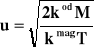
, (1.32)

czyli klasyczną postać podawaną przez literaturę z tego zakresu. Formuła (1.32) jest więc szczególnym przypadkiem formuły (1.31). Zależność krzywej kosztów K od wielkości partii można zilustrować wykresem (Rys. 1.3)

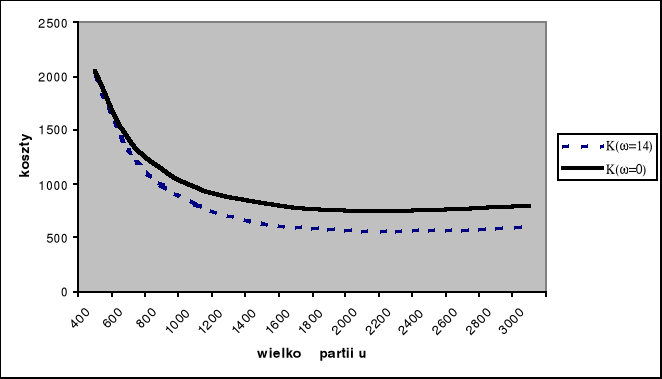
Rys. 1.3: Krzywe zależności sumy zmiennych kosztów magazynowania i kosztów odnawiania zapasu od wielkości partii dostawy

Wykres pokazuje, że krzywa ilustrująca funkcję K przy okresie odroczenia płatności  =0 osiąga minimum dla mniejszej wielkości partii dostawy, niż przy okresie odroczenia płatności większym od zera. Widać więc, że jest istotną zależność wielkości partii dostawy od okresu odroczenia płatności.

Jako optymalną wielkość zapasu Z przyjmiemy ostatecznie połowę optymalnej normy wielkości partii dostawy u*, czyli

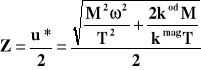
, (1.33)

ponieważ jest naturalne, że przy normie wielkości partii dostawy u* i ustabilizowanym w czasie tempie poboru towaru z magazynu średni zapas będzie się kształtował na poziomie połowy górnej granicy zapasu, czyli właśnie wielkości partii dostawy u*.

1.4. Parametry

Przystąpmy do ukazania przydatności praktycznej stworzonego modelu. Na początek musimy wprowadzić odpowiedni zespół wielkości liczbowych, niezmiennych w procesie obliczeniowym. Będą to parametry obliczeniowe.

Podstawowe parametry rzutujące na osiągane przez przedsiębiorstwo wyniki ekonomiczne przedstawiają się jak następuje (Tablica 1.1).

Tablica 1.1 Specyfikacja wartości liczbowych parametrów

Parametr	symbol	wielkość	jednostka
okres planowania	T	30	dni
stopa CIT	d	0,19
stopa VAT	v	0,22
okres odroczenia terminu płatności dla odbiorców	*	15	dni
okres odroczenia terminu płatności stosowany przez dostawców		7	dni
cena zaopatrzeniowa	p	4	zł/ jedn. towaru
średnia płaca brutto pracownika zatrudnionego na stałe	w1	2500	zł/ osoba
średnia płaca brutto pracownika fizycznego	w2	1300	zł/ osoba
wskaźnik zatrudnienia pracowników fizycznych na jednostkę towaru	l^fiz	0,001	osoby/ jedn. towaru
liczba pracowników stałych	L0	3	osoby
stopa kredytowa	c	0,09
koszty stałe	C^0	8000	zł
jednostkowy zmienny koszt magazynowania	k^mag	0,001	zł/ jedn. towaru w ciągu doby
koszt odnowienia zapasu	k^od	25	zł

Niezbędne dla obliczeń prowadzonych w procesie controllingu prospektywnego są poza tym parametry funkcji popytu na sprzedawany przez rozpatrywaną firmę towar. Można je uzyskać na drodze estymacji parametrów funkcji logistycznej, w oparciu o szereg liczbowy powstały w wyniku oszacowań popytu dla hipotetycznych poziomów ceny sprzedaży towaru. Zdolni do dokonania takich oszacowań powinni być zajmujący się marketingiem pracownicy firmy, znający mechanizm rynku danego towaru. W danym prostym przypadku szereg liczbowy powstanie w wyniku wielokrotnej odpowiedzi na zapytanie o poziom popytu dla różnych poziomów ceny.

Dla szeregu hipotetycznych poziomów ceny sprzedaży oszacowano więc poziom popytu, jak w tablicy (Tablica 1.2).

Tablica 1.2 Oszacowania popytu dla hipotetycznych poziomów ceny sprzedaży towaru

cena	Popyt
0	3850
1	3830
2	3790
3	3730
4	3660
5	3580
6	3470
7	3350
8	3200
9	3040
10	2850
11	2640
12	2410
13	2170
14	1920
15	1680
16	1445

Na tej podstawie, przy użyciu metody najmniejszych kwadratów, wyestymowano parametry logistycznej funkcji popytu, zapewniające najlepsze dopasowanie szeregu teoretycznego do przytoczonego wyżej (Tabl. 1.2), niejako empirycznego szeregu liczbowego. Uzyskano wartości parametrów, jak niżej.

		γ
3993,54	0,0341	0,24662

Parametry te kształtują krzywą popytu o następującym kształcie (Rys. 1.4)

Rys 1.4: Krzywa popytu w zależności od ceny sprzedaży towaru

Dysponując przytoczonymi wyżej parametrami funkcji popytu oraz opisem funkcyjnym można teraz przystąpić do procesu symulacji charakterystyki przedsiębiorstwa przy uwzględnieniu optymalizacji decyzji.

1.5. Proces symulacji charakterystyki stanu przedsiębiorstwa

Operując wyżej przedstawionym modelem matematycznym, który będziemy nazywać modelem przedsiębiorstwa, można prowadzić symulacje przyszłego jego stanu weryfikując formułowane każdorazowo hipotezy decyzyjne określające cenę sprzedaży towaru. Skoro dysponujemy przy tym parametrycznym rozwiązaniem problemu normy zapasu towaru - formuła (1.33) - będziemy każdorazowo automatycznie dostosowywać optymalizacyjnie poziom owej normy do warunków sprzedaży powodowanych przez strategię rynkową firmy mającą tu postać ceny. Powtarzając postępowanie symulacyjne można znajdziemy taką wersję decyzji cenowej, która okaże się lepsza od pozostałych hipotez decyzyjnych, ze względu na wynik finansowy przedsiębiorstwa.

Przystępując do przeprowadzenia postępowania symulacyjnego odpowiedzmy na początek na pytanie: Co by się stało, gdyby firma w nadchodzącym okresie operowała stosowaną wcześniej ceną sprzedaży równą x=14 zł za jednostkę towaru? Otóż wówczas stan przedsiębiorstwa - z uwzględnieniem liczbowych wartości parametrów uwidocznionych w Tablicy 1.1 - prezentowałby się, jak przedstawia to poniższy graf interakcji (Rys. 1.5a). Pamiętamy, że do wyliczenia kapitału obrotowego jest brana ta część zapasu, która realnie generuje zmienne koszty magazynowania, a więc u'/2. Jest to połowa wielkości określonej wzorem (1.25), bowiem tylko ta część normatywnego zapasu generuje średnio zamrożenie kapitału. W węźle grafu pokazującym wielkość zapasu pojawia się natomiast normatywny poziom zapasu określony w oparciu o formułę (1.33). Obraz przedsiębiorstwa oczywiście generuje się automatycznie po wprowadzeniu hipotezy dotyczącej ceny. Zabieg ten jest możliwy dzięki wykorzystaniu komputera.

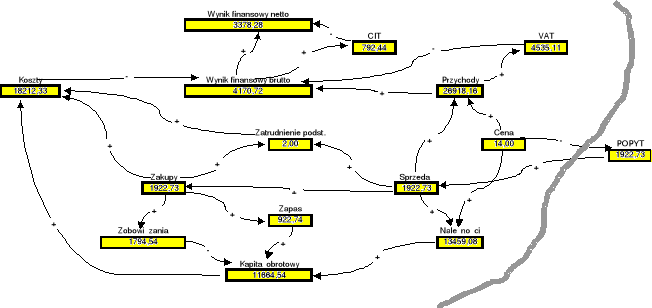
Rys. 1.5a: Charakterystyka stanu przedsiębiorstwa będąca następstwem przyjęcia ceny x=14 zł za jednostkę towaru przy optymalnej normie zapasu towaru

Widać, że tak działająca firma będzie osiągać dodatni wynik finansowy. Nie znaczy to jednak, że nie stać jej na więcej. Sprawdźmy jaki byłby skutek zwiększenia ceny z 14 do 16 zł za jednostkę towaru (Rys.1.5b).

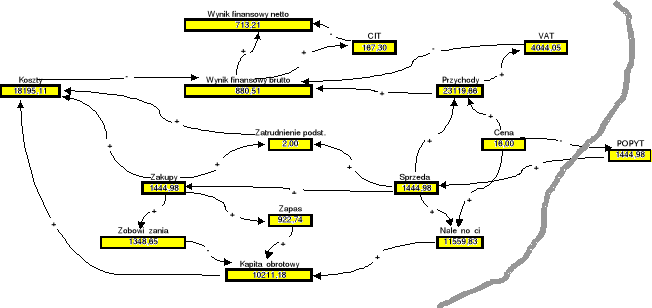
Rys. 1.5b: Charakterystyka stanu przedsiębiorstwa będąca następstwem przyjęcia ceny x=16 zł za jednostkę towaru przy optymalnej normie zapasu towaru

Widać teraz przede wszystkim, że istotnie zmieniły się wszystkie wielkości uwidocznione przez węzły grafu interakcji, a w szczególności wydatnie niższy okazał się wynik finansowy netto. Jest to rezultatem wyraźnego zmniejszenia się wielkości sprzedaży spowodowanego spadkiem popytu wynikłym z podwyższenia ceny sprzedaży towaru. Wystarcza to, by stwierdzić, iż przyjęta hipoteza okazała się mniej korzystna od poprzedniej. Poczyniony krok okazał się krokiem w złym kierunku.

Rozpatrzmy więc nową hipotezę. Niech w tym przypadku cena zostanie obniżona do 12 zł za jednostkę towaru. W rezultacie powstaje obraz stanu firmy jak na rysunku (Rys. 1.5c).

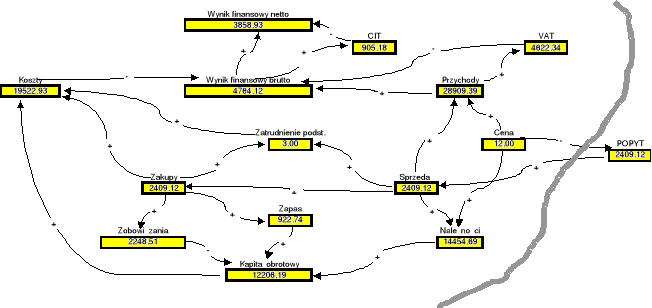
Rys. 1.5c: Charakterystyka stanu przedsiębiorstwa przy cenie x= 12 zł za jednostkę towaru, i optymalnej normie zapasu towaru

Kierunek zmiany ceny okazał się w tym przypadku właściwy. Widać, że wynik finansowy jest teraz wyraźnie wyższy. Podejmijmy więc próbę dalszego obniżenia ceny sprzedawanego towaru. Jej efekt zilustruje kolejna wersja grafu interakcji (Rys. 1.5d).

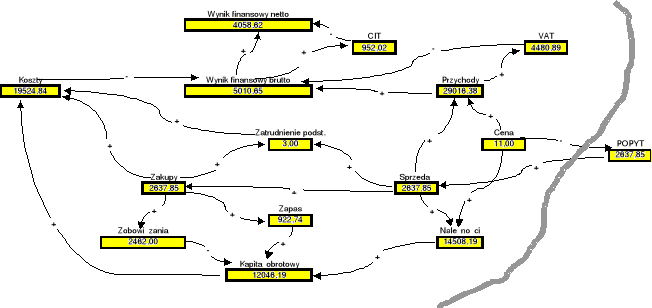
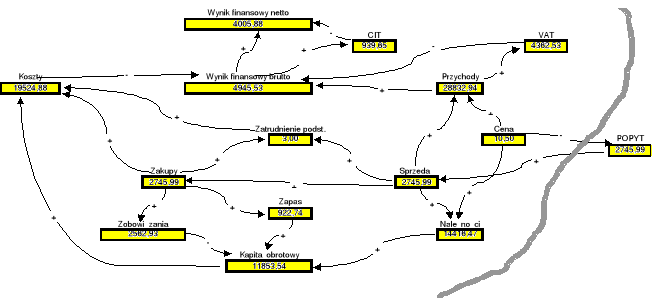
Rys. 1.5d: Charakterystyka stanu przedsiębiorstwa przy cenie x=11 zł za jednostkę towaru i optymalnej normie zapasu towaru

Hipotetyczna cena na poziomie 11 zł za jednostkę towaru prowadzi do kolejnej poprawy wyniku finansowego przedsiębiorstwa w stosunku do wyniku będącego konsekwencją ceny wyższej o złotówkę. Sprawdźmy więc jak ukształtuje się wynik finansowy przy cenie jeszcze niższej o złotówkę za jednostkę towaru. Otrzymamy stan ilustrowany grafem, jak niżej (Rys. 1.5e).

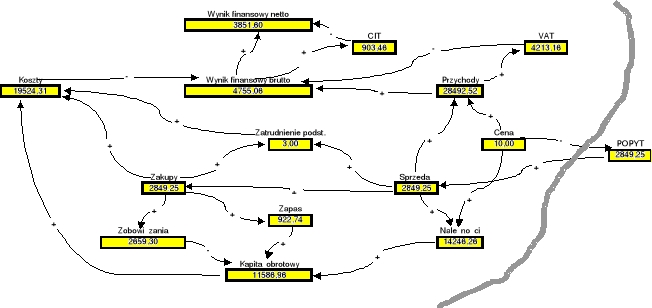
Rys. 1.5e: Charakterystyka stanu przedsiębiorstwa przy cenie x=10 zł za jednostkę towaru i optymalnej normie zapasu towaru

Możemy obserwować, że wynik finansowy jest teraz niższy niż uzyskany w poprzedniej symulacji. Cena 11 zł jest więc korzystniejsza od ceny 10 zł za jednostkę towaru. Spróbujmy jeszcze sprawdzić skutek zastosowania ceny pośredniej pomiędzy ceną 10 zł i 11 zł za jednostkę towaru. Niech więc wynosi 10,5 zł. Powstanie następujący obraz stanu firmy (Rys. 1.5f).

Rys. 1.5f: Charakterystyka stanu przedsiębiorstwa w rezultacie podyktowania ceny 10,5 zł za jednostkę towaru przy optymalnej normie zapasu towaru

Wynik finansowy jest teraz lepszy niż przy cenie 10 zł, ale nie tak dobry jak przy cenie 11 zł za jednostkę towaru. Można więc wysnuć wniosek, iż cena 11 zł za jednostkę jest bliska wartości najkorzystniejszej.

1.6. Optymalizacja strategii rynkowej przedsiębiorstwa w postaci ceny sprzedaży

Zamiast poszukiwać właściwej konfiguracji decyzji metodą powtarzalnych prób skorzystajmy teraz z szansy optymalizacji ceny sprzedaży towaru. Dysponujemy przecież stworzonym w tym celu instrumentem, jakim jest model optymalizacyjny (1.22). Dowiemy się wprost jaką powinna być cena sprzedaży towaru maksymalizująca wynik finansowy firmy.

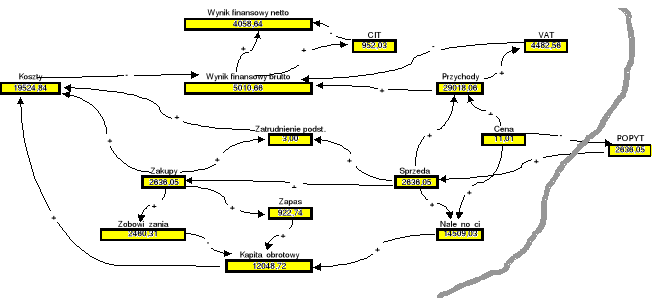
Rys. 1.6: Charakterystyka stanu przedsiębiorstwa będąca następstwem wzajemnie sprzężonej optymalizacji ceny sprzedaży towaru oraz normy zapasu towaru

Okazuje się (Rys. 1.6), iż cena 11 zł za jednostkę towaru jest ceną bardzo bliską optimum. Optymalna cena x=11,01 zł za jednostkę towaru zapewnia zysk netto WFN=4058 zł. Jest to zarazem uwarunkowane ustaleniem normy średniego zapasu na poziomie Z=922,74 jednostki towaru.

Przedstawiony przykład pokazuje, że deterministyczny model przedsiębiorstwa pozwala na znalezienie dobrego planu działalności. Przykład wyraża obrazowo literę i ducha controllingu prospektywnego, jako istotnego instrumentu wspomagającego zarządzanie operacyjne. Można go wykorzystywać zarówno w trybie ex post, jak i ex ante, z czego podstawowe znaczenie w zarządzaniu posiada ten drugi. Stąd wykorzystanie modelu w trybie prospektywnym jest w zarządzaniu podstawowe. Nie jest to jednak model uniwersalny. Każdy tego rodzaju model musi bowiem zawsze ściśle uwzględniać ogół cech i warunków działania przedsiębiorstwa, które w szczegółach nie są bynajmniej powtarzalne. W dalszym ciągu zostaną pokazane inne charakterystyczne przypadki przedsiębiorstw i właściwe dla nich wersje systemów controllingu prospektywnego.

Ten węzeł grafu zaznaczamy symbolicznie w otoczeniu przedsiębiorstwa, jako że popyt indukuje się poza przedsiębiorstwem.

Przyjęto, że stopa podatku VAT jest jednakowa dla wszystkich dóbr nabywanych przez przedsiębiorstwo oraz towaru stanowiącego przedmiot prowadzonej działalności handlowej.

Dura A., Optymalizacja zachowań rynkowych przedsiębiorstwa, Uczelniane Wydawnictwa Naukowo-Dydaktyczne AGH, Kraków 2005, s. 67

Nie jest to wartość kupowanej partii towaru, lecz koszt towarzyszący dostawie, np. koszt rozładunku.

Na marginesie można zauważyć, że przedstawione funkcje mają charakter rekurencyjny.

Kryński H., Badach A., Zastosowanie matematyki do podejmowania decyzji ekonomicznych, PWN 1976, ss. 268-270)

Sadowski Wiesław, Teoria podejmowania decyzji, PWE Warszawa 1976, s. 30

---