1. Dany jest wielomian ![]()
.
Wyznaczyć najmniejszy pierwiastek wielomianu
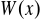
, jeśli wiadomo, ze jednym z jego pierwiastków jest liczba 2.Dla
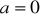
wyznaczyć zbiór wszystkich argumentów, dla których funkcja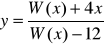
przyjmuje wartości nieujemne.Dla
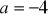
wyznaczyć największą wartość wielomianu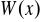
w przedziale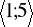
.
2. Funkcja f określona jest wzorem ![]()
Rozwiąż równanie
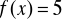
.Wyznacz przedziały monotoniczności funkcji f.
Oblicz najmniejszą i największą wartość funkcji w przedziale
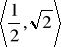
3. Dana jest funkcja ![]()
.
Dla
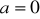
wyznaczyć najmniejszą i największą wartość tej funkcji w przedziale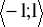
.Wyznaczyć zbiór wartości parametru
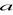
, dla których funkcja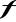
nie ma ekstremum.Wiadomo, że styczne do wykresu funkcji
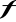
, poprowadzone w punktach przecięcia z osią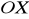
są równoległe. Wyznaczyć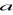
4. Funkcja jest określona wzorem .
Określ przedziały monotoniczności funkcji
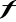
.Oblicz ekstrema tej funkcji.
Wyznacz równania stycznych do wykresu funkcji
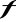
równoległych do prostej o równaniu .
5. Dana jest funkcja
Wyznaczyć przedziały monotoniczności tej funkcji.
Obliczyć ekstrema funkcji i podać najmniejsza i największą wartość funkcji w przedziale
Sporządzić wykres funkcji i zbadać liczbę pierwiastków równania w zależności od parametru m.
6. Wielomian W jest określony wzorem:
Napisać równanie stycznej do wykresu tego wielomianu, równoległej do prostej .
Wyznaczyć najmniejszą i największą wartość tego wielomianu w przedziale .
Wiadomo, że wielomian ma trzy różne pierwiastki, których suma równa się zero. Wyznaczyć m.
7. Dana jest funkcja , gdzie jest parametrem.
Dla k=1 wyznaczyć dziedzinę funkcji określonej wzorem
Wyznaczyć zbiór wartości parametru k, dla których nierówność zachodzi w zbiorze wszystkich liczb rzeczywistych
Wyznaczyć wszystkie wartości parametru k, dla których równanie ma dwa różne pierwiastki dodatnie.
8. Dana jest funkcja
Wyznaczyć zbiór wszystkich wartości parametru , dla których funkcja f przyjmuje wartości ujemne dla każdej liczby rzeczywistej x.
Dla rozwiązać równanie
Dla wykresy funkcji przecinają się w punktach A i B. Wyznaczyć na osi OX taki punkt P, że .
9. Dana jest funkcja ![]()
.
Wyznaczyć zbiór wszystkich argumentów, dla których funkcja
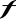
przyjmuje wartości większe od 5.Napisać równanie stycznej do wykresu funkcji
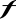
w punkcie o odciętej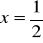
.Wyznaczyć najmniejszą i największą wartość funkcji
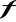
w przedziale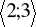
.
10. Dane są wielomiany: ![]()
, ![]()
, ![]()
.
Wyznaczyć zbiór wartości wielomianu
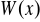
, dla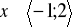
.Zbadać, czy istnieje taki wielomian
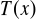
, że wielomian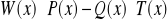
jest wielomianem zerowym. Odpowiedź uzasadnić.Rozwiązać nierówność
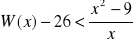
.
11. Dana jest funkcja postaci ![]()
.
Dla
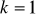
wyznaczyć zbiór wszystkich argumentów, dla których funkcja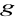
przyjmuje wartości mniejsze od 1.Dla
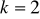
wyznaczyć przedziały monotoniczności funkcji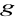
.
c) Wiadomo, że dla ![]()
funkcja ![]()
osiąga ekstremum lokalne. Zbadać, czy jest to minimum czy maksimum. Odpowiedź uzasadnić.
Dany jest wielomian
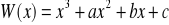
. Liczba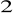
jest pierwiastkiem dwukrotnym, zaś liczba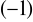
jest pierwiastkiem jednokrotnym tego wielomianu.
Wyznaczyć ekstrema lokalne wielomianu
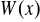
oraz uzasadnić, że dla każdego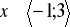
, wielomian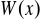
przyjmuje wartości nieujemne.Wyznaczyć wszystkie wartości parametru
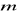
, dla których wielomian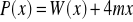
jest funkcją rosnącą w całej dziedzinie.Obliczyć pole trójkąta ograniczonego osiami układu współrzędnych i styczną do wykresu wielomianu
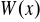
w punkcie o odciętej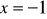
.
13. Dany jest wielomian postaci ![]()
.
Liczba
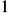
jest jednym z pierwiastków tego wielomianu. Oblicz najmniejszy pierwiastek wielomianu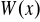
.Dla
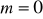
rozwiąż nierówność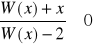
.Dla
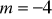
wyznacz najmniejszą i największą wartość wielomianu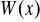
w przedziale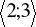
.
14. Dana jest funkcja ![]()
.
Rozwiąż nierówność
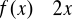
.Rozwiąż równanie
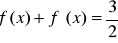
.Ustal liczbę rozwiązań równania
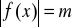
w zależności od parametru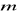
.
Wyszukiwarka
Podobne podstrony:
Pochodnesciagi, studia, Matma, Analiza Matematyczna, analiza, Ściągi
odp do egz, fizyka + matma UMK, matematyka, matma
Wyklady z matematyki II sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
Wykład 10Ściąga, MATMA, matematyka, Matma, Matma, Nowe, Różności
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Clocvium nr.1, materialy, Matematyka, MATMA
Wyklady z Matematyki czesc VI, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
Wyklady z Matematyki czesc IV, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
MATEMATYKA mini, MATMA, matematyka, Matma, Matma, Nowe, Różności
Laplace'a przekształcenie, materialy, Matematyka, MATMA
Wyklady z Matematyki czesc V, MATMA, matematyka, Matma, Matma, Stare, II semestr, Wykłady mini
POCHODNE, Matematyka, Liceum
Wykład11 całki, MATMA, matematyka, Matma, Matma, Nowe, Różności
Wyklady z matematyki IV sciaga, MATMA, matematyka, Matma, Matma, Stare, I semestr
więcej podobnych podstron