2. PRZESTRZEŃ LICZB ZESPOLONYCH

Definicja: Liczbami zespolonymi nazywamy uporządkowaną parę liczb rzeczywistych: a, b
. Oznaczamy je symbolem (a, b).

W zbiorze liczb zespolonych określamy w następujący sposób: dodawanie i mnożenie:

Def. Niech x = (a, b) ; y = (c, d), gdzie a, b, c, d
, wtedy:

x = y

* x +y =

x

Twierdzenie 1.

Operację dodawania oraz mnożenia w postaci (*) w zbiorze liczb zespolonych są przemienne, łączne oraz mnożenie jest rozdzielne względem dodawania, tzn. : dla dowolnych liczb zespolonych x, y, z zachodzą równości:

Zakładamy, że dla dowolnej liczby zespolonej x zachodzą równości:

Twierdzenie 2.

Dla dowolnej liczby zespolonej x istnieje dokładnie jedna liczba zespolona y, taka, że :

DOWÓD

Niech
wtedy
spełnia równanie

*Jeśli istniałoby
takie, że
to:

a więc
co przeczy przypuszczaniu
.

Def. Niech
. Wartością bezwzględną lub modułem liczby zespolonej x nazywamy liczbą nieujemną:

Twierdzenie 3

Niech x, y, z będą dowolnymi liczbami zespolonymi, wtedy:

1. jeżeli
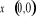
   , to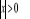
   ,
   

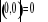
2. jeżeli
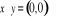
   , to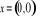
   , lub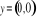
   , lub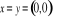
   

c) jeżeli
i
, to

DOWÓD

b) Niech

wtedy:

a więc:

Twierdzenie 4

Dla dowolnej liczby zespolonej
istnieje dokładnie jedna liczba zespolona y, taka, że:

Piszemy wtedy

DOWÓD

Niech
wtedy y określamy następująco:

gdyż:

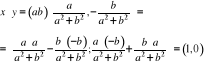
Twierdzenie 5

Jeżeli liczba zespolona
, to dla dowolnej liczby zespolonej y istnieje dokładnie jedna liczba zespolona z taka, że
Oznaczamy ją symbolem:

Ponieważ dla dowolnych liczb rzeczywistych a, b zachodzą równości:

, gdzie

więc liczby zespolone postaci
można utożsamić z liczbami rzeczywistymi: a.

Zatem zbiór liczb rzeczywistych
można traktować jako podzbiór zbioru liczb zespolonych.

Def.

Jednostką urojoną nazywamy liczbę zespoloną postaci:

zakładamy, że:

czyli:

PRZYKŁAD

Rozwiązywanie równania:

(*)
gdzie
,

Rozwiązanie: Pierwiastkami równania (*) są liczby zespolone

Twierdzenie 6

Jeżeli a, b są liczbami rzeczywistymi to liczba zespolona

gdyż

Jeżeli liczba zespolona ma postać

to "a" nazywamy częścią rzeczywistą liczby, a "b" częścią urojoną liczby "z"

Re z = a ("realis")

Im z = b ("imaginalis")

Twierdzenie 7

Jeżeli x, y są liczbami zespolonymi to zachodzi nierówność:

Def.

Liczbą sprzężoną do liczby zespolonej

nazywamy liczbę

Twierdzenie 8

Jeżeli x, y są liczbami zespolonymi, to:

1. 
   

2. 
   

3. 
   

4. 
   

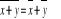
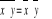
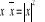
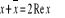
5. jeżeli
   , to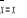
   

DOWÓD b)

Niech
,

Wtedy:

czyli

UWAGA !!!

Twierdzenie 9

Jeżeli a­­₁,...,a_n, b₁,....,b_n są liczbami zespolonymi to zachodzi nierówność Schwarza:

Liczbie zespolonej
odpowiada wzajemnie jednoznacznie na płaszczyźnie O XY punkt Z=(a,b). Płaszczyznę C, Której punktom zostały przyporządkowane dowolne liczby zespolone
;
nazywamy płaszczyzną liczbową.

Punktom na osi OX odpowiadają liczby zespolone postaci

, tzn. liczby rzeczywiste.

Punktom osi OY odpowiadają liczby zespolone postaci
, tzn. liczby urojone.

Def .Argumentem liczby zespolonej

nazywamy liczbę rzeczywistą
określoną równościami:

oraz

Piszemy:

Każda liczba zespolona
posiada przeliczalną ilość argumentów. Jeżeli
, jest argumentem

;

Argument liczby zespolonej
spełnia warunek:

nazywamy argumentem głównym liczby "z". Oznaczamy symbolem:

Arg z

Jeżeli
to

,

Możemy napisać

czyli

Jest to postać trygonometryczna liczby

Na odwrót, jeżeli
gdzie
, to

Uwaga.

Dwie liczby zespolone, różne od zera są równe wtedy i tylko wtedy, gdy są równe ich moduły, a argumenty różnią się o całkowitą wielokrotność 2π.

Jeżeli liczba zespolona:

czyli

to

Zatem dla
:

(*)

Powyższe równości rozumiemy następująco:

Dla dowolnych argumentów
,
istnieje argument iloczynu
oraz argument ilorazu
takie, że zachodzi twierdzenie (*).

Twierdzenie 10

Dla każdej liczby rzeczywistej
zachodzi równość:

1. 
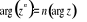
   przy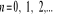
   

DOWÓD

1˚ Dla
równość (1) dowodzimy stosując indukcję zupełną

1. n=1
   

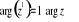
2. Zakładamy, że dla pewnego
   

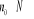
3. Wykażemy, że

Kolejno otrzymujemy:

2˚ Dla
mamy:

,

Ponieważ dla dowolnego
istnieje
(przy k=0) więc zachodzi równość (1), gdyż dla dowolnego
mamy:

3˚ Dla
podstawiamy
przy

wtedy

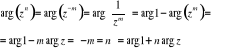
Wniosek

Zachodzi wzór de Moivre'a

dla

DOWÓD

Dla
mamy:

zatem dla
otrzymujemy:

gdzie

stąd

czyli

Z drugiej strony mamy:

czyli

dla

Każdą liczbę zespoloną "w" spełniającą równanie

gdzie
nazywamy pierwiastkiem n-tego stopnia lub n-tym pierwiastkiem liczby zespolonej "z", oznaczamy symbolem:

Twierdzenie 11

Jeżeli
to istnieje dokładni n różnych pierwiastków w_k , k=0,1,2,...,n-1, gdzie

Przy czym
oznacza pierwiastek arytmetyczny tj. liczbę nieujemną, a n-ta potęga równa się

Płaszczyzna rozszerzona

Niech będzie dana płaszczyzna
zbiór liczb zespolonych, wyznaczona przez układ prostokątny OXY

Sfera S o dowolnie ustalonym promieniu dodatnim
jest styczna do płaszczyzny C w punkcie (0,0). Prosta prostopadła do płaszczyzny C w punkcie (0,0) przecina sferę S w punkcie

Przyporządkowujemy każdemu punktowi
punkt
przy czym z' jest punktem przecięcia prostej przechodzącej przez z oraz N ze sferą S. Otrzymaliśmy odwzorowanie płaszczyzny C na sferę S, ale bez punktu N. Jest to tzw. rzut stereograficzny na sferę.

Odwzorowanie odwrotne do rzutu stereograficznego przyporządkowuje punktom sfery S bez punktu N punkty płaszczyzny C. Powyższe odwzorowania są funkcjami.

Uzupełnimy płaszczyznę C nowym elementem, któremu przy rzucie stereograficznym odpowiada punkt N sfery S. Ten nowy element nazywamy punktem w nieskończoności i oznaczamy symbolem ∞.

Prosta C uzupełniona punktem w nieskończoności nazywa się płaszczyzną domkniętą lub rozszerzoną. Oznaczmy ją przez:

Między skończonymi liczbami zespolonymi a punktem nieskończoności definiujemy następujące działania:

gdy

gdy

dla

III. CIĄGI I SZEREGI O WYRAZACH RZECZYWISTYCH.

1.Ciągi.

Będziemy sprawdzać ciągi o wyrazach rzeczywistych.

PRZYKŁAD

1. Ciąg arytmetyczny
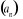
   gdzie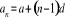
   ,
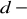
   różnica,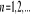
   

2. Ciąg geometryczny
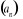
   , gdzie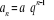
   ,
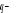
   iloraz,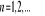
   

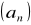
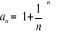
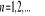
3. 
   ,
   ,
   

Def.

Mówimy, że
jest granicą ciągu
gdzie

jeżeli dla dowolnie małej liczby dodatniej
>0 istnieje taka liczba dodatnia N, że dla każdej liczby naturalnej
zachodzi implikacja

Piszemy wtedy:

Oznacza to, że:

Interpretacja geometryczna punktu

dla
,

Def.

Mówimy, że ciąg
ma granicę
,
jeżeli dla dowolnie dużej liczby dodatniej M istnieje liczba dodatnia N, taka, że dla każdej liczby naturalnej
zachodzi implikacja:

Piszemy wtedy:

Ciąg posiadający granicę skończoną nazywamy zbieżnym.

Ciąg, który nie jest zbieżny, czyli ma granicę nieskończoną lub nie posiada granicy skończonej, ani nieskończonej nazywamy rozbieżnym.

Granicą właściwą nazywamy granicę skończoną. Natomiast:
to granice niewłaściwe.

Ciąg
nazywamy granicznym jeżeli istnieje taka stała dodatnia M

WŁASNOŚCI CIĄGÓW ZBIEŻNYCH

1. Jeżeli ciąg
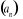
   jest zbieżny, to jest ograniczony.

DOWÓD

Zakładamy, że
to znaczy

Zachodzi nierówność:

czyli dla

Zatem oznaczając

Oznacza to, że M jest równe największej z liczb wymienionych w równaniu

otrzymujemy

zatem ciąg
jest ograniczony.

Na odwrót nie każdy ciąg ograniczony jest zbieżny.

Np. Ciąg
jest ograniczony, ale nie jest zbieżny.

2. Ciąg
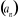
   posiada co najwyżej jedną granicę.

DOWÓD

Przypuśćmy, że
oraz
, przy czym niech np.
. Istnieje liczba rzeczywista r taka, że
. Biorąc
otrzymujemy

dla

oraz

dla

stąd dla
mamy

czyli

oraz

sprzeczność.

3. Jeżeli ciągi
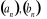
   są zbieżne odpowiednio do granic a, b to suma, iloczyn i różnica tych ciągów są także zbieżne oraz:

Jeżeli ponadto
dla

to

iloraz ciągów jest zbieżny.

DOWÓD

Suma:

Załóżmy, że
i
Niech
będzie dodatnią liczbą rzeczywistą i niech
będzie taką liczbą naturalną, że dla
zachodzi nierówność
. Niech
będzie taką liczbą naturalną, że dla
zachodzi nierówność
i niech
oznacza większą z liczb
Wtedy dla
zachodzą obydwie nierówności:

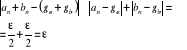
Znaczy to, że dla dostatecznie dużych liczb naturalnych n różnica
ma wartość bezwzględną mniejszą niż epsilon więc granica sumy równa się sumie granic.

Dla różnicy należy skorzystać z twierdzenia o zbieżności ciągu przeciwnego i powyższego twierdzenia o granicy sumy.

Iloczyn:

Ponieważ
,
więc

oraz

gdzie
jest stałą tak dobraną, że

,
,

Stąd dla
mamy:

czyli

Z twierdzenia o granicy iloczynu wynika wniosek:

Jeżeli ciąg
jest zbieżny, to ciąg c·a_n też jest zbieżny

gdzie c - stała

Twierdzenie 1 (Twierdzenie o trzech ciągach)

Jeżeli ciągi
są zbieżne, przy czym
oraz

to

DOWÓD

Z założeń wynika, że:

oraz

Zatem dla
zachodzą nierówności:

czyli

a więc

PRZYKŁAD

Znaleźć

przy
wyrazy ciągu prowadzą do wyrażenia nieoznaczonego typu

Zachodzą następujące oszacowania:

Z twierdzenia o trzech ciągach wynika, że granica równa się 5.

WŁASNOŚCI CIĄGÓW MAJĄCYCH GRANICE NIEWŁAŚCIWE

Jeżeli ciąg
posiada granicę niewłaściwą, to ciąg ten jest nieograniczony. Twierdzenie odwrotne nie jest prawdziwe Np. ciąg
, gdzie
jest nieograniczony oraz nie posiada granicy ani właściwej (skończonej), ani niewłaściwej.

Dla ciągów mających granice niewłaściwe - ∞ lub +∞ zachodzi twierdzenie o jednoznaczności.

Przy formułowaniu twierdzeń o działaniach arytmetycznych, dla granic niewłaściwych należy wykluczyć wyrażenia nieoznaczone.

Np. Jeżeli ciągi
posiada granicę oraz nie zachodzi

to ciąg
ma granicę oraz

1. Jeżeli ciąg
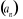
   ma granicę niewłaściwą oraz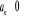
   dla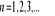
   

to:

DOWÓD

Jeżeli
to dla każdego
istnieje
taki, że

dla

Jeżeli
to dla każdego
istnieje
taki, że

dla

w każdym przypadku mamy:

dla
gdzie

czyli dla

więc

2. Jeżeli
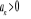
   dla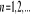
   oraz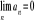
   , to

a jeżeli
dla
oraz
, to

DOWÓD

Jeżeli
oraz
, to

oznacza to, że:

dla

czyli

Twierdzenie o trzech ciągach przenosi się na przykłady granic nieskończonych.

Badając granice: sumy, różnicy, iloczynu lub ilorazu ciągów mających granice:
otrzymujemy tzw. wyrażenia nieoznaczone:

,
,
,
,
,

W tych przypadkach szukając granicy należy uwzględnić własności wyrazów ciągu: przez odpowiednie przekształcenia usunąć nieoznaczoność.

11

---