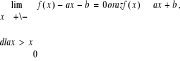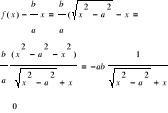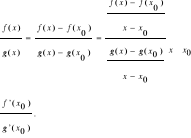Przykład: Szybkość reakcji chemicznej w czasie od =0sek do =10sek jest dana zależnością s= s(t)=2 -3 +1 Kiedy prędkość reakcji maleje, a kiedy rośnie? Kiedy prędkość reakcji jest najmniejsza, a kiedy największa? Rozwiązanie: s`(t)= 2·3 -3·2t=6 -6t=6t (t-1) ys'=s'(t) s'(t)=0<=>( =0, =1) Prędkość reakcji maleje, gdy s,'(t)≤0, tzn dla t <0,1>. Prędkość reakcji rośnie, gdy s'(t)>0, tzn dla t <1,10>. Ponieważ: s(t)= (2 -3 +1= (2-3 + )=+ s(t)=- , oraz s(t)=2 -3 +1=0 dla t'=1 2 -3 +1\t-1=2 -t-1 czyli s(t)= 2 -3 +1=(2 -t-1)(t-1), 2 -t-1 =3 t''= =1 t'''= =-1\2 s(t)=2(t-1)(t+1\2)(t-1)=2(t-1 (t+1\2) s“=(t)=12t-6, s'(t)=6 -6t=0<=> =0, =1 s”(0)=-6 - max funkcji s=s(t), s”(1)=6 - min funkcji więc wykres prędkości s=s(t) jest następujący: Prędkość reakcji jest najmniejsza w chwili t=1s, a największa w t=10s s=2 -3 +1 Do badania wypukłości (wklęsłości) funkcji służą następujące twierdzenia: TWIERDZENIE 4 Niech funkcja f będzie określona na przedziale otwartym (a,b) oraz niech f posiada skończoną pochodną f' na (a,b). Na to, by funkcja f była wypukła (wklęsła) na (a,b) potrzeba i wystarcza by pochodna f' była niemalejąca(nierosnąca) na (a,b). TWIERDZENIE 5 Niech funkcja f będzie określona na przedziale (a,b) oraz niech f posiada skończoną pochodną f” na (a,b). Na to, by funkcja f była wypukła (wklęsła) na (a,b) potrzeba i wystarcza by ( ) Def: Mówimy, że punkt P=P( jest punktem przegięcia krzywej y=f(x), która jest wykresem funkcji y=f(x), jeżeli w zmienia się charakter wypukłości funkcji, tj. funkcja z wypukłej staje się wklęsłą lub na odwrót. Np.: f(x)=arctgx posiada w (0,0) punkt przegięcia:

TWIERDZENIE 6 Jeżeli funkcja f : (a,b) → posiada skończoną pochodną f” (x) w pewnym otoczeniu punktu oraz wykres funkcji f ma punkt przegięcia to teza mówi . TWIERDZENIE 7 Jeżeli funkcja f posiada w otoczeniu skończone pochodne do rzędu (n-1)-tego włącznie przy czym oraz skończoną pochodną (n-tego rzędu) , gdzie n>2 to w punkcie wykres funkcji f ma punkt przegięcia, gdy n jest liczbą nieparzystą.Np: f(x)= dla ; f' (x)= 3 , f” (x) = 6x, f” (0)=0 - warunek konieczny istnienie punktu przegięcia f'''(x)=6 0 - warunek dostateczny istnienia punktu przegięcia Uwaga. Niech funkcja rzeczywista f będzie określona na niepustym podzbiorze X = V {- } Obok punktów, w których funkcja f posiada maximum lokalne lub minimu lokalne mogą w dziedzinie X isnieć punkty, w których funkcja f przyjmuje wartość największą lub najmniejszą. ASYMPTOTY:Niech będzie dana krzywa y=f(x) określona i ciągła na x , gdzie X jest przedziałem skończonym lub, nieskończonym, o wartościach rzeczywistych. Jeżeli odległość punktu krzywej od pewnej prostej dąży do 0 i jest różna od 0 przy oddalaniu się punktu do (lub do ) lub przy to prosta ta nazywa się asymptotą krzywej y=f(x). Zbadamy 3 rodzaje asymptot: asymptoty poziome Na to by przy prosta y=b była asymptotą krzywej y=f(x), f (x) R potrzeba i wystarcza by: │f(x)=b│=0 oraz f(x) b Co jest równoważne warunkowi oraz f(x) wtedy prostą y=b nazywamy asymptotą poziomą krzywej y=f(x) np.: f(x)=arctgx, x

Asymptoty poziome asymptoty pionowe: Niech funkcja rzeczywista f będzie określona w pewnym otoczeniu punktu : ( - z wyjątkiem[lub w przedziale ( - ), ( w przedziale , + )]. Mówimy, że funkcja f ma asymptotę pionową x= w punkcie (lewostronną asymptotę pionową x= , prawostronną asymptotę pionową x= ), gdy lub Np.: funkcje y= lnx posiada prawostronną asymptotę pionową x=0. asymptoty ukośne Niech funkcja rzeczywista f będzie określona dla x> lub x< , . Mówimy, że prosta y=ax+b jest asymptotą ukośną fukcji f przy , gdy Lub TWIERDZENIE 8 Niech funkcja f będzie określona dla x> , . Prosta y=ax+b jest asymptotą ukośną, której y=f(x) przy istnieją skończone granice oraz Uwaga:Twierdzenie 8 przestaje być prawdziwe, gdy przedział można zastąpić przedziałem oraz zamiast napisać . Przykład: Dana jest hiperbola o równaniu: , wiadomo, że wykres tej funkcji jest następujący:

Część hiperboli, która leży powyżej osi Ox ma równanie dla , proste są asymptotami krzywej y=f(x), gdzie: przy 5) Wyrażenia nieoznaczone. 5.1. Wyrażenia nieoznaczone typu TWIERDZENIE 1 Jeżeli: a) funkcje f, g są określone na przedziale <a,b> b) c) istnieją skończone pochodne przy czym to Dowód:, Ponieważ istnieją skończone pochodne , więc funkcje f, g są ciągłe w , tzn: czyli Ze względu na , więc ze wzoru Taylora wynika, że istnieje takie otoczenie zawarte w przedziale <a,b>, że dla zatem dla mamy

---