Politechnika Śląska

Wydział Automatyki Elektroniki i Informatyki

Kier. Informatyka

grupa IV

TEMAT : WYZNACZANIE SZEROKOŚCI PRZERWY ENERGETYCZNEJ PÓŁPRZEWODNIKA METODĄ TERMICZNĄ (TERMISTOR)

Aleksander Biela

Marcin Bury

Wstęp teoretyczny:

Przewodnictwo elektryczne półprzewodników związane jest z ruchem elektronów w paśmie przewodnictwa oraz dziur w paśmie walencyjnym. W bardzo niskich temperaturach pasmo przewodnictwa nie zawiera elektronów, zaś pasmo walencyjne jest nimi całkowicie zapełniane. W półprzewodnikach już w temperaturze pokojowej przechodzi do pasmo przewodnictwa pewna część elektronów. Proces pojawiania się elektronów w paśmie walencyjnym pod wpływem wzrostu temperatury nosi nazwę generacji termicznej par dziura-elektron.

Przerwa energetyczna jest to odstęp pomiędzy pasmem przewodnictwa, a pasmem walencyjnym. Szerokość tej przerwy oznacza minimalną ilość energii, która musi być dostarczona elektronom, aby przeszły one do pasma przewodnictwa.

W półprzewodnikach przerwa energetyczna jest względnie mała(mniejsza niż 2[eV]), w związku z czym istnieje szansa przeskoku elektronów do pasma przewodnictwa na skutek wzbudzeń cieplnych.

Stanowisko pomiarowe:

W układzie pomiarowym materiał półprzewodnika obecny jest w termistorze. Stanowisko składa się z dwóch termistorów umieszczonych w aluminiowym bloczku, wyznacza się szerokość przerwy dla każdego z termistorów osobno. Bloczek aluminiowy jest podgrzewany przy pomocy tranzystora bipolarnego. Natężenie prądu płynącego przez tranzystor regulowane jest przy pomocy potencjometru. Do pomiaru temperatury wykorzystano czujnik temperatury połączony z miernikiem cyfrowym. Oporność termistorów są mierzone za pomocą mierników cyfrowych.

Przebieg ćwiczenia:

1. Ustalenie z Prowadzącym temperatury granicznej ogrzewania termistorów oraz krok temperaturowy z jakim będą wykonywane pomiary.

2. Zmierzenie oporności termistorów w zastanej temperaturze.

OGRZEWANIE TERMISTORÓW

3. Ustawianie przy pomocy potencjometru żądanej temperatury.

4. Odczekanie aż temperatura bloczka osiągnie żądaną temperaturę.

5. Odczytanie oporności obu termistorów.

6. Przeprowadzenie podobnych pomiarów dla wyższych temperatury

CHOODZENIE BLOCZKA

7. Ustawienie przy pomocy potencjometru temperaturę równą zastanej temperaturze.

8. temperaturze miarę samorzutnego ochładzania się aluminiowego bloczka zanotowano oporność termistorów z zadanym krokiem temperatury.

OGRZEWANIE TERMISTORÓW
T(°C)	R1(kΩ)	R2(kΩ)
24,3	21,77	28,7
30	16,85	25,3
32	15,37	23
34	13,72	20,5
36	12,58	18,8
38	11,59	17,4
40	10,63	15,9
42	9,72	14,5
44	9	13,5
46	8,33	12,4
48	7,7	11,3
50	6,97	10,9
52	6,48	9,6
54	5,92	8,9
56	5,55	8,2
58	5,13	7,5
60	4,68	7
62	4,37	6,4
64	3,98	5,9
66	3,71	5,5
68	3,542	5,1
70	3,229	4,7

CHŁODZENIE TERMISTORÓW
T(°C)	R1(kΩ)	R2(kΩ)
70	3,229	4,7
68	3,5	5,2
66	3,84	5,6
64	4,13	6
62	4,45	6,6
60	4,81	7,1
58	5,17	7,6
56	5,62	8,3

Opracowanie wyników:

1. Na podstawie otrzymanych wyników pomiarowych sporządzono wykres zależności oporu R od temperatury T dla obu termistorów.

2. Słupki błędu zaznaczono za pomocą:

u(T)= 0,1 °C (dane przyrządu)

gdzie:

W - zmierzona wartość

C - rozdzielczość (1Ω dla R < 4 kΩ, 10 kΩ dla 4 Ω<R<40 kΩ)

OGRZEWANIE TERMISTORÓW				CHŁODZENIE TERMISTORÓW
R1(kΩ)	ΔsR1	R2(kΩ)	ΔsR2	R1(kΩ)	ΔsR1	R2(kΩ)	ΔsR2
21,77	0,25416	29	0,312	3,229	0,105832	4,7	0,1176
16,85	0,2148	25,3	0,2824	3,5	0,1216	5,2	0,1216
15,37	0,20296	23	0,264	3,84	0,1248	5,6	0,1248
13,72	0,18976	20,5	0,244	4,13	0,128	6	0,128
12,58	0,18064	18,8	0,2304	4,45	0,1328	6,6	0,1328
11,59	0,17272	17,4	0,2192	4,81	0,1368	7,1	0,1368
10,63	0,16504	15,9	0,2072	5,17	0,1408	7,6	0,1408
9,72	0,15776	14,5	0,196	5,62	0,1464	8,3	0,1464
9	0,152	13,5	0,188
8,33	0,14664	12,4	0,1792
7,7	0,1416	11,3	0,1704
6,97	0,13576	10,9	0,1672
6,48	0,13184	9,6	0,1568
5,92	0,12736	8,9	0,1512
5,55	0,1244	8,2	0,1456
5,13	0,12104	7,5	0,14
4,68	0,11744	7	0,136
4,37	0,11496	6,4	0,1312
3,98	0,11184	5,9	0,1272
3,71	0,10968	5,5	0,124
3,542	0,108336	5,1	0,1208
3,229	0,105832	4,7	0,1176

3. Wykres zależności logarytmu naturalnego oporności od odwrotności temperatury.

lnR=f(1/T)

OGRZEWANIE TERMISTORÓW
1/T	T(K)	R1(kΩ)	lnR1	R2(kΩ)	ln R2
0,00336191	297,45	21,77	3,080533	29	3,367296
0,003298697	303,15	16,85	2,824351	25,3	3,230804
0,003277077	305,15	15,37	2,732418	23	3,135494
0,003255738	307,15	13,72	2,618855	20,5	3,020425
0,003234676	309,15	12,58	2,532108	18,8	2,933857
0,003213884	311,15	11,59	2,450143	17,4	2,85647
0,003193358	313,15	10,63	2,36368	15,9	2,766319
0,003173092	315,15	9,72	2,274186	14,5	2,674149
0,003153082	317,15	9	2,197225	13,5	2,60269
0,003133323	319,15	8,33	2,119863	12,4	2,517696
0,00311381	321,15	7,7	2,04122	11,3	2,424803
0,003094538	323,15	6,97	1,941615	10,9	2,388763
0,003075504	325,15	6,48	1,868721	9,6	2,261763
0,003056702	327,15	5,92	1,778336	8,9	2,186051
0,003038129	329,15	5,55	1,713798	8,2	2,104134
0,00301978	331,15	5,13	1,635106	7,5	2,014903
0,003001651	333,15	4,68	1,543298	7	1,94591
0,002983739	335,15	4,37	1,474763	6,4	1,856298
0,002966039	337,15	3,98	1,381282	5,9	1,774952
0,002948548	339,15	3,71	1,311032	5,5	1,704748
0,002931262	341,15	3,542	1,264692	5,1	1,629241
0,002914177	343,15	3,229	1,172172	4,7	1,547563

CHŁODZENIE TERMISTORÓW
1/T	T(K)	R1(kΩ)	lnR1	R2(kΩ)	ln R2
0,002914177	343,15	3,229	1,172172	4,7	1,547563
0,002931262	341,15	3,5	1,252763	5,2	1,648659
0,002948548	339,15	3,84	1,345472	5,6	1,722767
0,002966039	337,15	4,13	1,418277	6	1,791759
0,002983739	335,15	4,45	1,492904	6,6	1,88707
0,003001651	333,15	4,81	1,570697	7,1	1,960095
0,00301978	331,15	5,17	1,642873	7,6	2,028148
0,003038129	329,15	5,62	1,726332	8,3	2,116256

4. Metodą regresji liniowej dopasowano prostą do punktów pomiarowych:

• dla ogrzewania termistorów:

Pierwszy termistor:

y = 4144,3x - 10,931

Drugi termistor:

y = 3747,4x - 9,1805

• dla chłodzenia termistorów:

Pierwszy termistor:

y = 4111,5x - 10,814

Drugi termistor:

y = 3755,8x - 9,2083

5. Na podstawie parametrów prostej wyznaczono szerokość przerwy energetycznej dla obu termistorów:

gdzie:

a - współczynnik kierunkowy wykresu zależności ln R od 1/T

k - stała Boltzmanna (1,38∙10^-23)

• Dla ogrzania termistorów:

Pierwszy termistor:

Drugi termistor:

• Dal chłodzenia termistorów:

Pierwszy termistor:

Drugi termistor:

TERMISTOR 1		TERMISTOR 2
OGRZEWANIE	CHŁODZENIE	OGRZEWANIE	CHŁODZENIE

6. Korzystając z prawa propagacji niepewności obliczono niepewność u(E) dla obu termistorów. Wartość u(a) odczytano i podzielono przez √3 w programie Microsoft Excel.

TERMISTOR1		TERMISTOR 2
ogrzewanie	ochładzanie	ogrzewanie	ochładzanie

Do obliczeń średniej ważonej wykorzystano wzór:

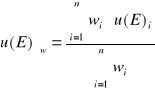
TERMISTOR1		TERMISTOR 2
ogrzewanie	ochładzanie	ogrzewanie	ochładzanie

Ostatecznie szerokość przerwy energetycznej wyniosła:

TERMISTOR 1: E=0,71(22)[eV]

TERMISTOR 2: E=0,65(13)[eV]

Wnioski:

Ćwiczenie miało na celu wyznaczenie szerokość przerwy energetycznej termistorów.

Z obliczeń można zauważyć, że termistory nie są jednakowe, gdyż posiadają różne szerokość przerwy energetycznej. Porównując otrzymane wyniki z tablicowymi, możliwe, że w TERMISTORZE 1 użyto antymonku galu jako materiału półprzewodnikowego, którego E=0,726[eV]. Natomiast w TERMISTORZE 2 materiałem półprzewodnikowym jest german, którego E=0,67[eV].Błędy, które powstały w trakcie wykonywania ćwiczenia wynikają z niedokładności przyrządów pomiarowych, niedokładności odczytu oraz możliwej utracie właściwości fizycznych jak i chemicznych pod upływem czasu badanych materiałów półprzewodnikowych.

---