WYZNACZNIK
Każdej macierzy kwadratowej przyporządkowujemy liczbę nazywaną jej wyznacznikiem.
Definicja
Wyznacznik macierzy kwadratowej
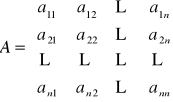
oznaczamy 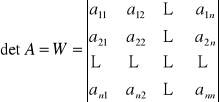
a jego wartość określamy:
jeżeli
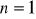
, o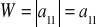
;jeżeli
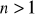
, to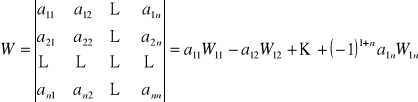
, gdzie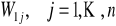
oznacza wyznacznik otrzymany z wyznacznika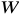
przez pominięcie pierwszego wiersza i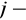
tej kolumny.
Uwaga
Uogólniając, wyznacznik otrzymany z wyznacznika ![]()
przez pominięcie ![]()
tego wiersza i ![]()
tej kolumny oznaczamy symbolem ![]()
i nazywamy podwyznacznikiem wyznacznika ![]()
( minorem elementu ![]()
.
Definicja
Algebraicznym dopełnieniem elementu ![]()
nazywamy iloczyn ![]()
Wyznacznik macierzy jest równy sumie iloczynów elementów pierwszego wiersza tego wyznacznika przez ich algebraiczne dopełnienie ![]()
.
Definicja
Stopniem wyznacznika macierzy nazywamy stopień macierzy.
WŁASNOŚCI WYZNACZNIKÓW
Twierdzenie
Jeżeli w wyznaczniku zamienimy wiersze na kolumny, to wartość wyznacznika nie zmieni się.
Jeżeli w wyznaczniku przestawmy dwa wiersze (kolumny), to wartość wyznacznika zmieni się na przeciwną.
Jeżeli elementy pewnego wiersza (kolumny) wyznacznika są zerami, to wyznacznik jest równy 0.
Jeżeli elementy pewnego wiersza (kolumny) są proporcjonalne (w szczególności równe) do elementów innego wiersza (kolumny) wyznacznika, to wyznacznik jest równy 0.
Jeżeli elementy pewnego wiersza (kolumny) wyznacznika pomnożymy przez liczbę
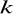
, to wartość wyznacznika też zostanie pomnożona przez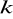
.Jeżeli do elementów pewnego wiersza (kolumny) dodamy elementy innego wiersza (kolumny) tego wyznacznika pomnożone przez tę samą liczbę, to wartość wyznacznika nie zmieni się.
Suma iloczynów elementów
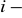
tego wiersza (kolumny) przez algebraiczne dopełnienie elementów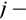
tego wiersza (kolumny) wyznacznika jest równa temu wyznacznikowi gdy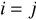
lub jest równa 0 gdy
;
tzn.
jeżeli 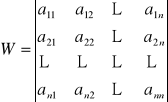
, to
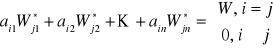
,
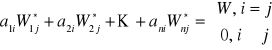
.
Jeżeli
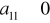
, to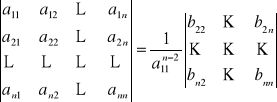
, gdzie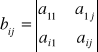
,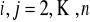
.
METODY OBLICZANIA WYZNACZNIKÓW
Metoda Laplace'a
Z własności (7) wynika, że wyznacznik jest równy sumie iloczynów elementów dowolnego wiesza (kolumny) przez ich algebraiczne dopełnienie, tzn.:
![]()
(rozwinięcie wyznacznika według ![]()
tego wiersza)
lub
![]()
(rozwinięcie wyznacznika według ![]()
tej kolumny).
Uwaga
Łatwo obliczyć wyznacznik rozwijając go według wiersza lub kolumny, w której jest dużo zer.
Metoda Chio ( metoda obniżania stopnia)
Metoda wynika z własności (8) wyznacznika.
Metoda Sarrusa (n=3)
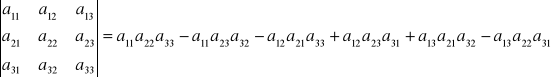
Definicja
Macierzą odwrotną do macierzy ![]()
nazywamy taką macierz ![]()
(o ile istnieje), dla której ![]()
, gdzie ![]()
macierz jednostkowa.
Definicja
Macierz, której wyznacznik jest różny od zera nazywamy macierzą nieosobliwą. Macierz, której wyznacznik jest równy zero nazywamy macierzą osobliwą.
Twierdzenie
Jeżeli ![]()
jest macierzą kwadratową, której wyznacznik ![]()
jest różny od zera (macierzą nieosobliwą), to istnieje dokładnie jedna macierz odwrotna do macierzy ![]()
i jest ona określona wzorem: 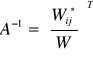
, gdzie ![]()
algebraiczne dopełnieniem elementu ![]()
.
RZĄD MACIERZY
Definicja
Minorem nazywamy wyznacznik, utworzony z macierzy ![]()
przez pominięcie pewnej liczby wierszy i pewnej liczby kolumn.
Definicja
Rzędem macierzy nazywamy największy stopień jej niezerowego minora.
Przyjmujemy, że rząd dowolnej macierzy zerowej jest równy zero.
Rząd macierzy 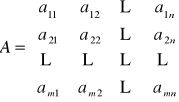
jest równy ![]()
, co zapisujemy
![]()
, gdy istnieje minor stopnia ![]()
tej macierzy różny od zera, a wszystkie
minory stopnia wyższego są równe zeru;
stąd
![]()
.
Twierdzenie
Jeżeli w macierzy:
zamienimy wiersze na kolumny,
przestawimy dwa wiersze (kolumny),
pomnożymy elementy pewnego wiersza (kolumny) przez tę samą, różną od zera, liczbę,
do elementów pewnego wiersza (kolumny) dodamy elementy innego wiersza (kolumny) pomnożone przez tę samą liczbę,
pominiemy wiersz (kolumnę) złożony z samych zer,
pominiemy jeden z dwu wierszy (kolumn) o elementach proporcjonalnych,
to rząd macierzy nie zmieni się.
UKŁADY RÓWNAŃ LINIOWYCH
Definicja
Układem ![]()
równań liniowych o ![]()
niewiadomych ![]()
nazywamy
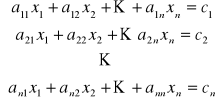
.
Rozwiązaniem tego układu jest ![]()
liczb ![]()
spełniających powyższe równania.
Układ ten możemy zapisać w postaci macierzowej ![]()
, przyjmując:
![]()
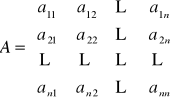
, 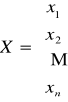
, C=![]()
.
Wyznacznik macierzy ![]()
nazywamy wyznacznikiem głównym układu.
Twierdzenie (Twierdzenie Cramera)
Jeżeli wyznacznik główny ![]()
układu ![]()
równań liniowych o ![]()
niewiadomych ![]()
jest różny od zera, to układ ten ma dokładnie jedno rozwiązanie i jest ono określone tzw. wzorami Cramera: ![]()
, gdzie ![]()
oznacza wyznacznik otrzymany z wyznacznika ![]()
przez zastąpienie ![]()
tej kolumny kolumną wyrazów wolnych ![]()
.
Definicja
Układem ![]()
równań liniowych o ![]()
niewiadomych ![]()
nazywamy
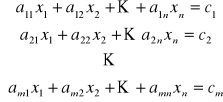
.
Rozwiązaniem tego układu jest ![]()
liczb ![]()
spełniających powyższe równania.
Układ ten możemy zapisać w postaci macierzowej ![]()
, przyjmując:
![]()
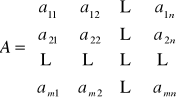
, 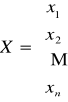
, C=![]()
.
Definicja
Macierzą rozszerzoną (uzupełnioną) ![]()
układu ![]()
równań liniowych o ![]()
niewiadomych ![]()
jest macierz powstała z macierzy ![]()
po dołożeniu do niej (jako ostatnią kolumnę) kolumny wyrazów wolnych, tzn.
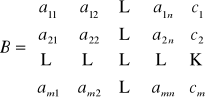
.
Twierdzenie ( Twierdzenie Kroneckera-Capelliego)
Układ ![]()
![]()
równań liniowych o ![]()
niewiadomych ![]()
ma rozwiązanie wtedy i tylko wtedy, gdy rzędy macierzy ![]()
i macierzy rozszerzonej ![]()
są równe
![]()
,
przy tym:
jeżeli
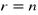
, to układ ma jedno rozwiązanie,jeżeli
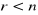
, to układ ma nieskończenie wiele rozwiązań i są one zależne od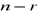
parametrów.
Uwaga
Z twierdzenia wynika, że jeżeli ![]()
, to układ nie ma rozwiązań (jest sprzeczny).
Definicja
Układ równań liniowych ![]()
nazywamy układem jednorodnym, jeżeli w układzie tym ![]()
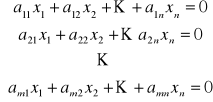
dla ![]()
lub ![]()
.
W przeciwnym wypadku układ nazywamy układem niejednorodnym.
Uwaga
Zauważmy, że każdy układ jednorodny ma rozwiązanie zerowe ![]()
.
Wyszukiwarka
Podobne podstrony:
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
Wyznaczanie przyspieszenie ziemskiego za pomocą wahadła matematycznego
1 Wyznaczanie wartości przyspieszenia ziemskiego g przy użyciu wahadła matematycznego instr przys
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCA WAHADŁA MATEMATYCZNEGO, Fiza
Elementy statystyki matematycznej wykorzystywane do opracowywania wielkości wyznaczanych, Geodezja i
Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła matematycznego, PWSZ Nowy Sącz, I semestr, W
Matematyka [ macierze][ szeregi], matematyka macierze, Liczenie wyznaczników w macierzy 3x3
Wyznaczanie przyspieszenia ziemskiego metodą wahadła matematycznego
Projekt wyznacenie przyśpieszenia ziemskiego za pomocą układu wahadla matematycznego
ZAdania z matematyki, MACIERZE I WYZNACZNIKI-2010, MACIERZE I WYZNACZNIKI - ZADANIA
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO, FIZYKA(1)
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO, FIZYKA(1)
Równania i nierówności z parametrem i z wartością bezwzględną.Wyznaczanie pierwiastków równania., Ma
matematyka, Roz uk równań wyznaczników m, Rozwiązywanie układów równań metodą wyznaczników
Wyznaczanie przyspieszenia ziemskiego wahadłem matematycznym
WŁ wyznaczników, Prywatne, Budownictwo, Matematyka
WYZNACZANIE OGNISKOWEJ SOCZEWEK ZA POMOCĄ ŁAWY OPTYCZNEJ0-2, Matematyka - Fizyka, Pracownia fizyczna
więcej podobnych podstron