Ćwiczenie nr 7 |
TEMAT :ADSORPCJA NA GRANICY FAZ ROZTWÓR-GAZ. IZOTERMA ADSORPCJI GIBBSA. |
||
|
|
||
|
|
||
|
|
|
|
Ocena : |
Podpis : |
||
Napięcie powierzchniowe.
Cząsteczki cieczy w warstewce powierzchniowej znajdują się pod działaniem sił wyciągających ją do wnętrza cieczy. W skutek tego obok ciśnienia wewnętrznego występuje zjawisko napięcia powierzchniowego.
Istniejące siły między cząsteczkami cieczy działają w kierunku zmniejszania powierzchni odgraniczającej ciecz od pary. (na powierzchni siły te, nie są wysycone).
Przemieszczenie cząsteczek z wnętrza cieczy na powierzchnię wymaga wkładu energii , toteż możemy mówić o energii powierzchniowej cieczy, czyli ciecz wykazuje dążność do zmniejszania liczby cząsteczek na swej powierzchni do wielkości możliwie najmniejszą w danych warunkach . W warstwie powierzchniowej musza zatem istnieć siły, zmniejszające powierzchnię które działają wzdłuż powierzchni w każdym jej punkcie. Siły te są niezależne od wielkości powierzchni, lecz jedynie od charakteru cieczy i temperatury, dlatego każda ciecz będzie wykazywać charakterystyczne dla siebie wartości napięcia powierzchniowego.
![]()
(1)
gdzie:σ-napięcie powierzchniowe.
Z równania (1) wynika, że napięcie powierzchniowe jest liczbowo równe pracy wytworzenia powierzchni jednostkowej i ma wymiar erg/cm2 czyli dyna/cm.
Metoda pęcherzykowa pomiaru napięcia powierzchniowego.
Metoda ta polega na pomiarze ciśnienia niezbędnego, do przerwania błonki powierzchniowej cieczy , przez pęcherzyki powietrza. Wymagane do tego ciśnienie Pm. na końcu kapilary równa się sumie ciśnienia hydrostatycznego Ph na poziomie h i ciśnienia kapilarnego Pς.
Pm= Ph + Pσ (2)
Ciśnienie hydrostatyczne na poziomie h oblicza się za pomocą wzoru:
Ph = ρ gh (3)
gdzie: ρ- gęstość cieczy w danej temperaturze .
Ciśnienie kapilarne, zależy od napięcia powierzchniowego oraz promienia pęcherzyka. Wyznacza się je z porównania pracy zmiany objętości i powierzchni:
p d V=σ d s (4)
![]()
(5)
Doświadczalne oznaczenie ciśnienia:
![]()
(6)
stąd:
![]()
(7)
gdzie: ρ-gęstość cieczy manometrycznej w danej temperaturze
h -głębokość zanurzenia kapilary
r -promień kapilary
Pm -zmierzone ciśnienie manometryczne.
Izoterma adsorpcji Gibbsa.
Powierzchnia ma szczególne właściwości, które odgrywają między innymi zasadniczą rolę w zjawisku adsorpcji, gdyż cząsteczki na powierzchni cieczy maja inny potencjał termodynamiczny niż cząsteczki w głębi cieczy.
W oparciu o zasady termodynamiczne , dotyczące adsorpcji na granicy faz roztwór-gaz przeprowadził Gibbs. Rezultaty ujęte zostały w postaci równania mającego charakter ogólny i stanowiącego podstawę fizykochemicznych zjawisk powierzchniowych. Równanie Gibbsa zwane izotermą adsorpcji ustala zależność miedzy nadmiarem stężeniowym Γi tej substancji, jej potencjałem chemicznym i napięciem powierzchniowym i ma postać:
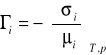
(8)
gdzie: ai oznacza aktywność i-tej substancji.
Ponieważ ![]()
, równanie /8/ można zapisać w postaci:
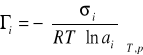
(9)
lub
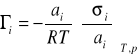
(10)
Jeżeli przyjmiemy, że dla roztworów rozcieńczonych ai≈ci otrzymamy:
![]()
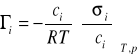
(11)
Równanie to-(11)- przedstawia najczęściej spotykaną postać izotermy adsorpcji Gibbsa.
Obliczanie adsorpcji z równania izotermy Gibbsa.
Za pomocą równania izotermy Gibbsa można obliczyć i wykreślić przebieg funkcji Γi=f(ci), z przebiegu funkcji σ=f(ci) Obliczenia te można wykonać w różny sposób.
Najczęściej przeprowadza się tzw. wykreślne różniczkowanie krzywej σ=f(ci) które daje wartości pochodnych![]()
.Różniczkowania te można wykonać w dwojaki sposób:
1. W różnych punktach krzywej σ=f(ci) wykreślamy styczne do niej doprowadzając je do przecięcia się z osią odciętych. Styczne te tworzą z tą osią kąty α1,α2......... Tangensy tych kątów dają odpowiednie wartości pochodnej ![]()
dla różnych stężeń substancji i w roztworze. Mnożąc uzyskane wartości ![]()
, przez odpowiednie wyrażenia - ci /RT otrzymuje się, szukane nadmiary powierzchniowe
W różnych punktach krzywej σ=f(c) wykreślamy styczne do niej, przedłużając je do przecięcia się, z osią rzędnych. Przez punkty, w których narysowano styczne, prowadzimy proste równoległe do osi odciętych, doprowadzając je do przecięcia z osią rzędnych. Styczne i odpowiednie proste równoległe do osi odciętych wyznaczają na osi rzędnych odcinki z. Z zależności geometrycznej wynika:
![]()
=![]()
(12)
czyli
z = -ci![]()
(13)
oraz
Γi=![]()
(14)
OPRACOWANIE WYNIKÓW:
Wyznaczanie promienia kapilary:
![]()
gdzie:
σ- napięcie powierzchniowe wody = 0,07198 [N/m]
pm- ciśnienie manometryczne [mmH2O];[Pa]
ρ-gęstość wody = 998 [kg/m3]
g- przyśpieszenie ziemskie = 9,81 [m/s2]
h- wysokość słupa cieczy = 0,018 [m]
![]()
Obliczanie napięcia powierzchniowego:
![]()
![]()
![]()
stężenieC2H2OH [%wag] |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
ciś. manometr. pm [mmH2O] |
8,0 |
6,4 |
5,7 |
5,1 |
4,4 |
4,2 |
4,0 |
3,7 |
3,5 |
napięcie pow. [dyna/cm] |
72,75 |
58,38 |
48,47 |
41,97 |
35,54 |
31,4 |
29,55 |
28,82 |
27,01 |
Obliczanie aktywności alkoholu etylowego:
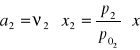
![]()
Obliczanie nadmiarów powierzchniowych etanolu metodą analityczną:
![]()
![]()
![]()
![]()
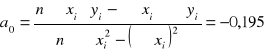
![]()
![]()
![]()
![]()
T=293K
R=8,314 J/mol
(![]()
)T,p= kba2b-1
l.p |
stężenie C2H2OH [%wag] |
x1 |
x2 |
ρ [g/cm3] |
p2 [mmHg] |
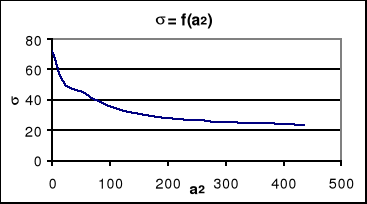
a2 |
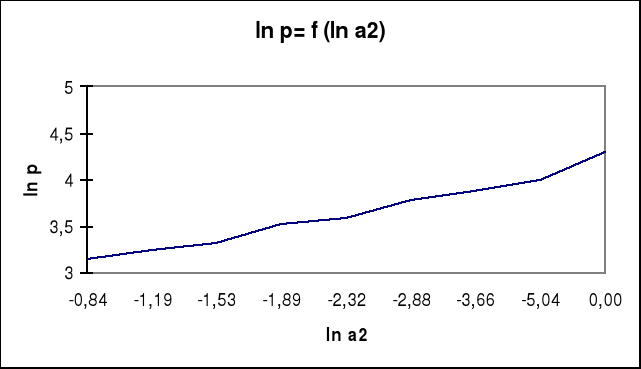
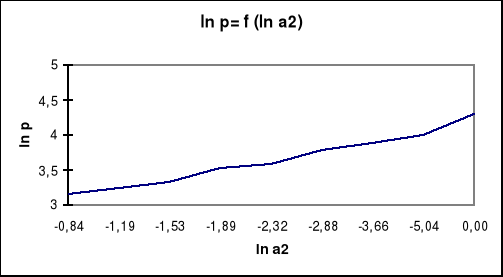
ln a2 |
σ
|
Γ2 [10-6] |
0 |
1,00 |
0,00 |
0,998 |
0,00 |
0 |
0 |
72,75 |
0 |
|
10 |
0,958 |
0,042 |
0,982 |
6,7 |
6,45*10-3 |
-5,044 |
58,38 |
4,86 |
|
20 |
0,911 |
0,089 |
0,969 |
12,6 |
25,7*10-3 |
-3,661 |
48,47 |
3,71 |
|
30 |
0,857 |
0,143 |
0,954 |
17,1 |
56,1*10-3 |
-2,881 |
41,49 |
3,19 |
|
40 |
0,794 |
0,206 |
0,935 |
20,7 |
97,8*10-3 |
-2,325 |
35,54 |
2,86 |
|
50 |
0,719 |
0,281 |
0,914 |
23,5 |
151*10-3 |
-1,890 |
31,40 |
2,63 |
|
60 |
0,631 |
0,369 |
0,891 |
25,6 |
217*10-3 |
-1,528 |
29,55 |
2,45 |
|
70 |
0,524 |
0,476 |
0,868 |
28,0 |
306*10-3 |
-1,184 |
28,82 |
2,29 |
|
80 |
0,391 |
0,609 |
0,843 |
31,2 |
436*10-3 |
-0,830 |
27,01 |
2,14 |
5.Obliczanie nadmiarów powierzchniowych metodą graficzną:
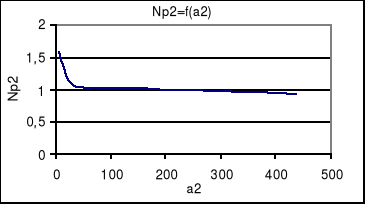
a2 |
|
z |
Γ2 [10-6] |
0 |
0 |
0 |
0 |
6,45*10-3 |
-1,187 |
7,66*10-3 |
3,14 |
25,7*10-3 |
-0,300 |
7,71*10-3 |
3,16 |
56,1*10-3 |
-0,188 |
10,5*10-3 |
4,33 |
97,8*10-3 |
-0,094 |
9,19*10-3 |
3,77 |
151*10-3 |
-0,053 |
8,00*10-3 |
3,28 |
217*10-3 |
-0,025 |
5,43*10-3 |
2,23 |
306*10-3 |
-0,013 |
3,98*10-3 |
1,63 |
436*10-3 |
-0,005 |
2,18*10-3 |
0,89 |
Obliczanie
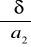
![]()
Obliczanie z:
![]()
Obliczanie Γ2:
![]()
OPRACOWANIE WYNIKÓW:
Napięcie powierzchniowe obliczamy ze wzoru:
![]()
gdzie:
δx- napięcie powierzchniowe badanej cieczy [N/m]
δw- napięcie powierzchniowe wody [N/m.] =
h1- głębokość zanurzenia kapilary [m.] = 0,018 [m]
ρ-gęstość wody
g- przyśpieszenie ziemskie [m/s2]
h- wysokość słupa cieczy [m]
σ = 72,8 [dyn/cm] =72,8∗10-3 N/m
![]()
![]()
![]()
![]()
![]()
Obliczanie napięcia powierzchniowego:
![]()
![]()
![]()
stężenieC2H2OH [%wag] |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
ciś. manometr. pm [mmH2O] |
84 |
66 |
60 |
56 |
48 |
46 |
40 |
38 |
36 |
napięcie pow. [dyna/cm] |
72,8 |
54,34 |
48,19 |
44,09 |
35,88 |
33,83 |
27,68 |
25,63 |
23,58 |
3.Obliczanie aktywności alkoholu etylowego:
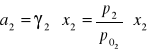
![]()
gdzie:
![]()
prężność alkoholu nad jego roztworem wodnym
![]()
-prężność alkoholu nad czystym etanolem
4.Obliczanie nadmiarów powierzchniowych etanolu metodą analityczną:
![]()
![]()
![]()
![]()
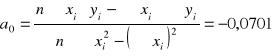
![]()
![]()
![]()
![]()
T=293K
R=8,314 J/mol
(![]()
)T,p= kba2b-1
l.p |
stężenie C2H2OH [%wag] |
x1 |
x2 |
ρ [g/cm3] |
p2 [mmHg] |
a2 |
ln a2 |
σ [dyna/cm]
|
Γ2 [10-6] |
0 |
1,00 |
0,00 |
0,998 |
0,00 |
|
0 |
72,8 |
|
|
10 |
0,458 |
0,042 |
0,9982 |
6,7 |
|
-5,0515 |
54,34 |
|
|
20 |
0,911 |
0,089 |
0,969 |
12,6 |
|
-3,6691 |
48,19 |
|
|
30 |
0,857 |
0,143 |
0,954 |
17,1 |
|
-2,8896 |
44,09 |
|
|
40 |
0,794 |
0,206 |
0,935 |
20,7 |
|
-2,3341 |
35,88 |
|
|
50 |
0,719 |
0,281 |
0,914 |
23,5 |
|
-1,8965 |
33,83 |
|
|
60 |
0,631 |
0,369 |
0,891 |
25,6 |
|
-1,5385 |
27,68 |
|
|
70 |
0,524 |
0,476 |
0,868 |
28,0 |
|
-1,194 |
25,63 |
|
|
80 |
0,391 |
0,609 |
0,843 |
31,2 |
|
-0,83956 |
23,58 |
|
5.Obliczanie nadmiarów powierzchniowych metodą graficzną:
a2 |
|
z |
Γ2 [10-6] |
0 |
0 |
0 |
0 |
6,4541*10-3 |
-0,4715 |
3,0431*10-3 |
1,5776 |
2,5720*10-2 |
-0,1074 |
2,7623*10-3 |
1,1339 |
5,6085*10-2 |
-0,0466 |
2,6136*10-3 |
1,0729 |
9,7803*10-2 |
-0,0257 |
2,5135*10-3 |
1,0318 |
1,5146*10-1 |
-0,0161 |
2,4385*10-3 |
1,0010 |
2,1666*10-1 |
-0,01098 |
2,3789*10-3 |
0,9765 |
3,0569*10-1 |
-0,0076 |
2,3232*10-3 |
0,9537 |
4,3579*10-1 |
-0,0052 |
2,2661*10-3 |
0,9302 |
Obliczanie
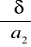
![]()
Obliczanie z:
![]()
Obliczanie Γ2:
![]()
wykres zależności napięcia powierzchniowego od stężenia
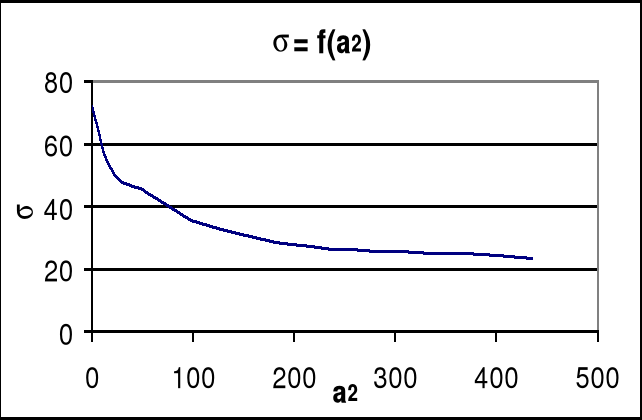
wykres zależności napięcia powierzchniowego od aktywności alkoholu
zależność nadmiarów powierzchniowych od aktywności
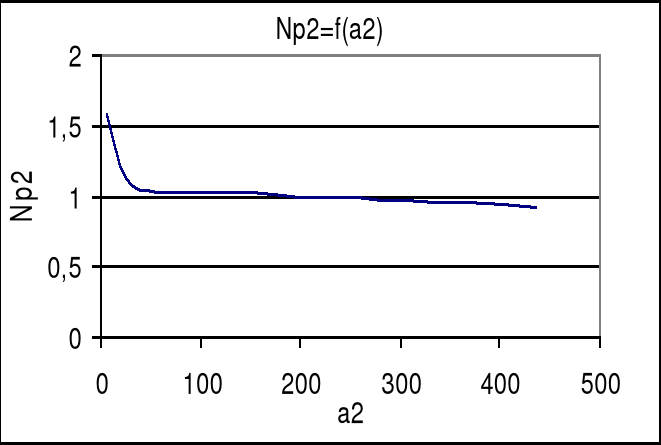
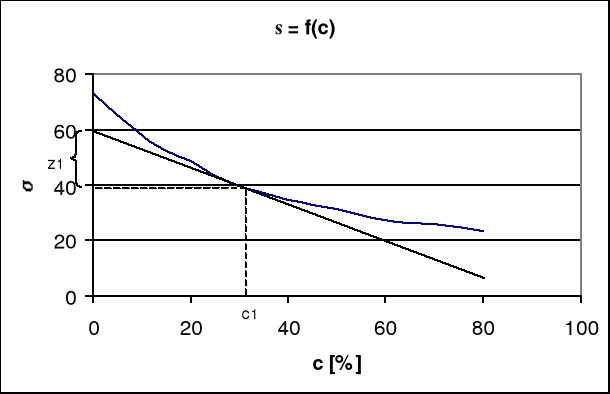
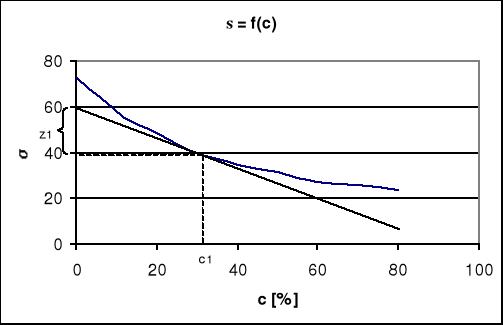
c1
z1
c1
Wyszukiwarka
Podobne podstrony:
cw 5 sprawozdanie, Studia, Politechnika
cw 15, Studia, Politechnika
cw 10m, Studia, Politechnika
cw 5m, Studia, Politechnika
charakterystyka sprężyn(1), Studia Politechnika Poznańska, Semestr IV, Wytrzymałość Materiałów, Labo
cw 7(2), Studia, Politechnika
ćw. 3 - spawanie elektrodą otuloną, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 2 s
sprawozdanie cw 2, Studia - Politechnika Opolska, Semestr 6, NSI
sprawozdanie fiza 6 (cw. 50), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
Sprawozdanie fiza 5 (ćw.71), 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza,
Cw.1 Wirownica, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, Fizyka, sprawka od Mateusza
Cw.2 Wahadło, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, Fizyka, sprawka od Mateusza,
Robimy elementy belkowe, Studia Politechnika Poznańska, Semestr VI, Systemy MES, Lab-Projekt Wojtek,
Charakterystyka sprężyn, Studia Politechnika Poznańska, Semestr IV, Wytrzymałość Materiałów, Laborki
CW 7211, 1 STUDIA - Informatyka Politechnika Koszalińska, finish, fizyka1, fiza, Fizyka 2, 72(dodatk
Sprawozdanie metrologia cw. 1, studia, studia Politechnika Poznańska - BMiZ - Mechatronika, 3 semest
więcej podobnych podstron