Analiza mechanizmu dźwigniowego
Synteza strukturalna i geometryczna mechanizmu
W poniższym podpunkcie zostały przyjęto, wymiary mechanizmu oraz ograniczenia warunkujące jego prawidłową prace i działanie. Również założyłem początkowe położenie mechanizmu, oraz prędkości i przyspieszenie członu napędzającego.
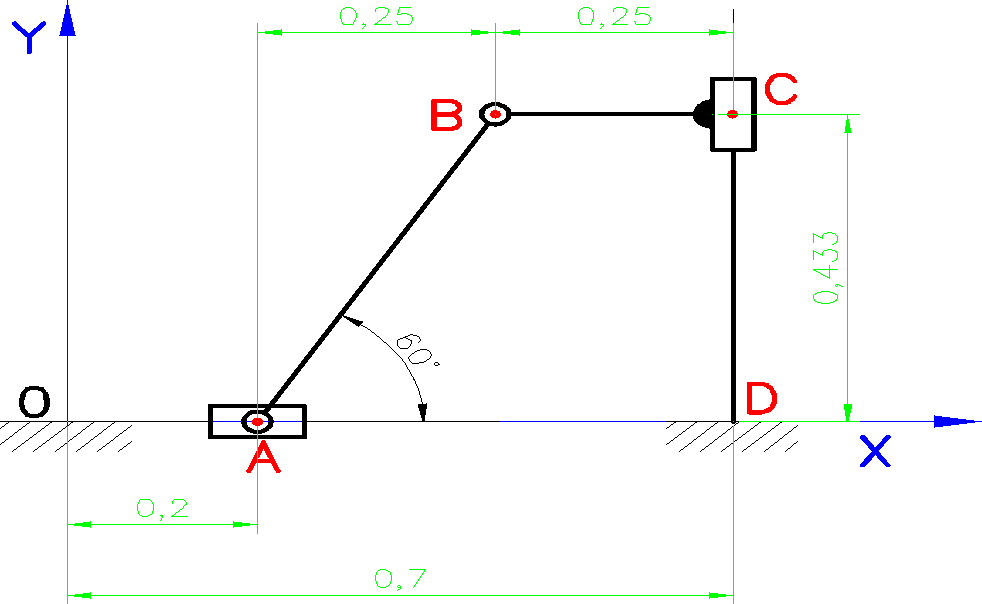
Przyjęto wymiary:
|AB|=0,5[m]
|BC|=0,25[m]
|OD|=0,7 [m]
oraz dla jednego położenia mechanizmu:
|0A|=0,2[m]
|CD|=0,433[m]
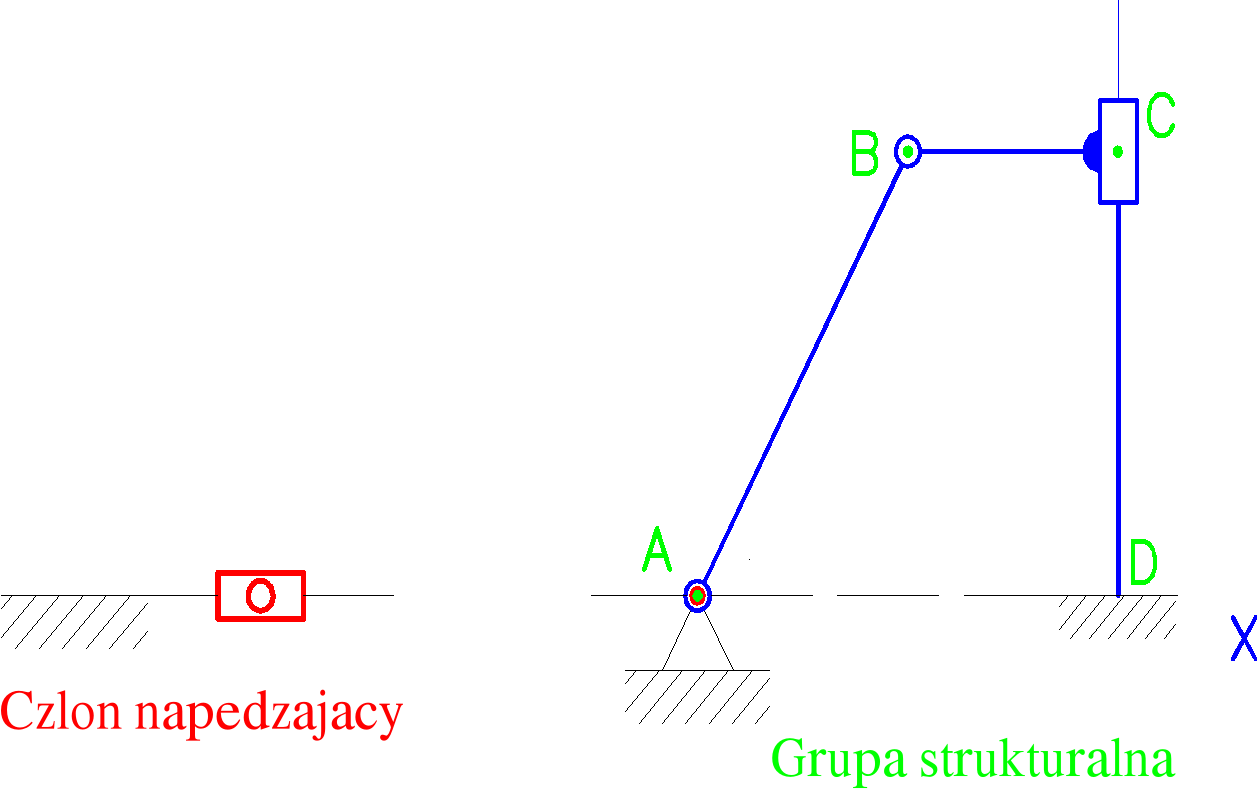
Zdefiniowano prędkość i przyspieszenie członu napędzającego:
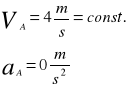
Wyznaczenie ruchliwości mechanizmu, podział na grupy strukturalne oraz klasyfikacja mechanizmu.
Podział na grupy strukturalne.
Grupa strukturalna analizowanego mechanizmu jest klasy II
Ruchliwość mechanizmu:
![]()
w- ruchliwość mechanizmu
n- liczba członów mechanizmu
i- klasa par występujących w łańcuchu kinematycznym
p4- para kinematyczna klasy czwartej
p5- para kinematyczna klasy piątej
Wyznaczenie ruchliwości analizowanego mechanizmu
n= 3
p4=0
p5=4
![]()
Ruchliwość mechanizmu w=1
Analiza kinematyczna mechanizmu.
Analiza kinematyczna mechanizmu metoda grafoanalityczna.
Analiza kinematyczna wykonana jest dla jednego wybranego położenia mechanizmu.
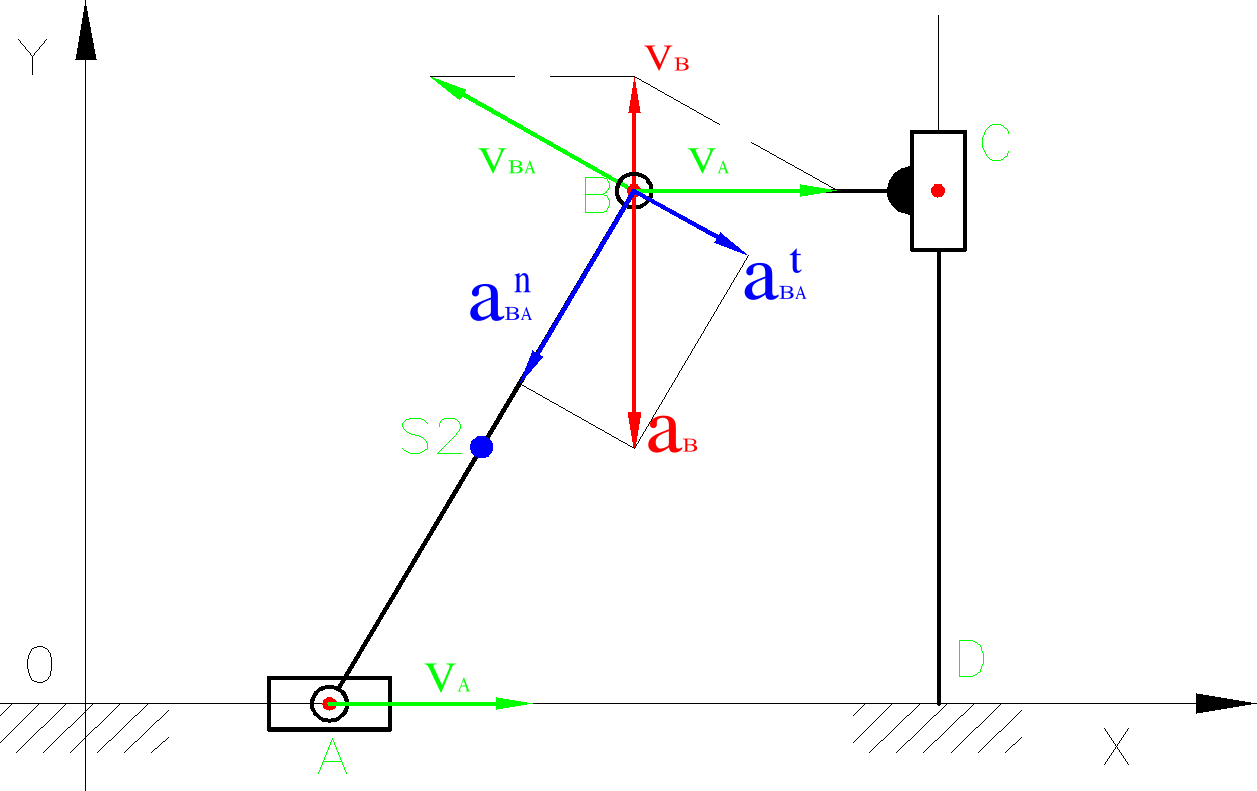
Grafoanalityczna analiza prędkości mechanizmu.
Wyznaczenie prędkości VA(zdefiniowanie))
Prędkość VA=4![]()
Wyznaczenie prędkości VB
![]()
Wektor prędkości ![]()
jest równoległy | CD|
Wektor prędkości ![]()
jest prostopadły |AB|
Wyznaczanie prędkości punktu VC
![]()
Prędkość (m2) środka masy członu napędzającego, równa jest prędkości pkt. punktu D
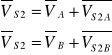
Przyjęcie podziałki rysunkowej dla planu prędkości:
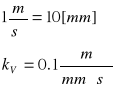
Plan prędkości
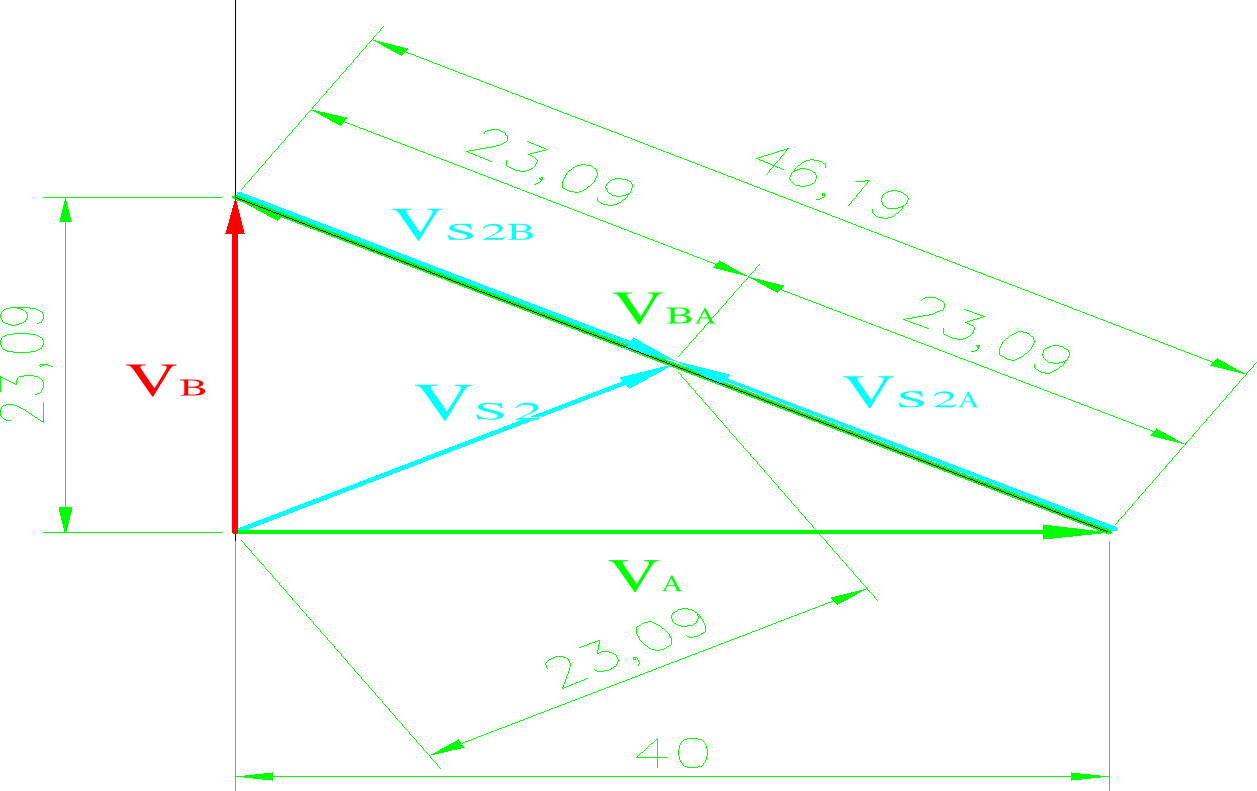
Z planu prędkości odczytano następujące wartości:

Wyznaczenie prędkości kątowej członu drugiego:
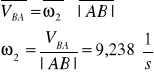
Grafoanalityczna analiza przyśpieszeń mechanizmu.
Przyspieszenie punktu A (członu napędzającego) zostało zdefiniowane w punkcie pierwszym i wynosi:
![]()
Równania przyśpieszeń mechanizmu dla poszczególnych punktów:
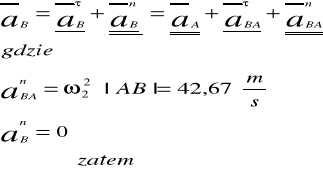

![]()
Przyspieszenie (m2) środka masy członu napędzającego, równe jest przyspieszeniu pkt. punktu D
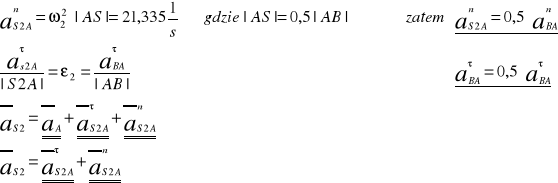
Przyjęcie podziałki rysunkowej dla planu przyśpieszeń:
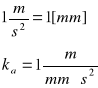
Plan przyśpieszeń
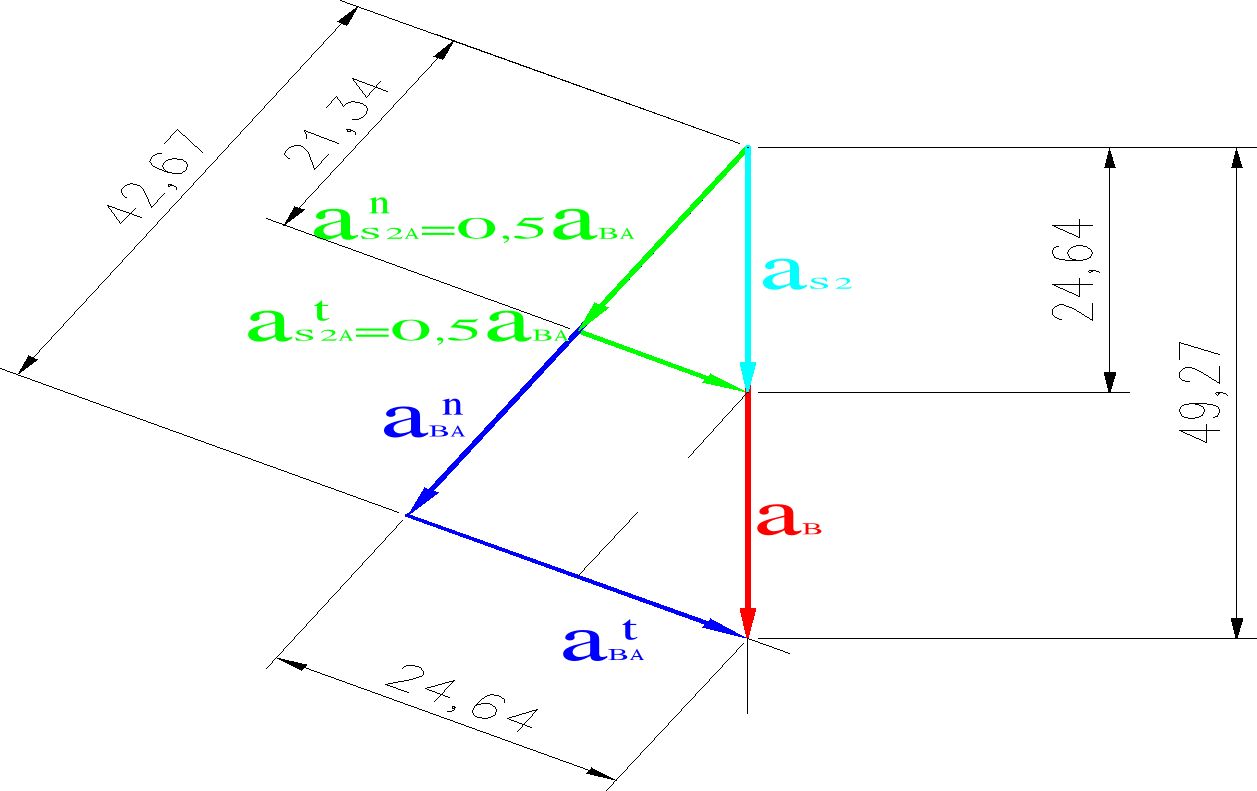
Z planu przyspieszeń odczytano następujące przyspieszeni:

Wyznaczenie przyspieszenia kątowego członu drugiego:
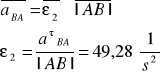
Analiza kinematyczna mechanizmu metoda analityczna.
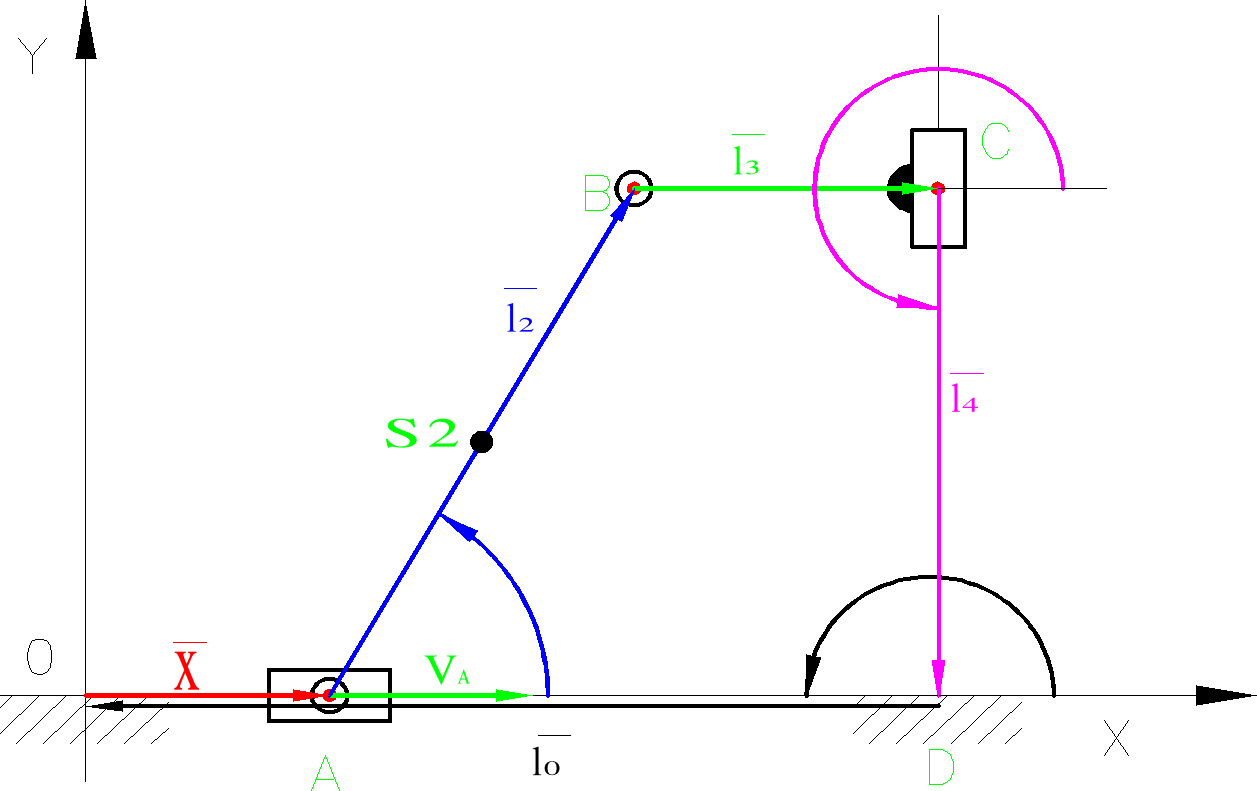
x(t) jest to wektor definiujący ruch członu napędzającego:
l4(t) , φ2(t), są funkcjami zmiennymi w czasie
poniższe funkcje są funkcjami stałymi i nie zależą od czasu, przyjmują zawsze stalą wartość:
φx(t)=0◦ l2(t)=0,5[m]
φ3(t)=0◦ l3(t)=0,25[m]
φ4(t)=270◦ l0(t)= 0,7 [m]
φ0(t)=180 ◦
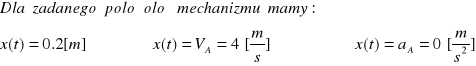
Wyznaczenie ogólnych równań ruchu
Analiza prędkości mechanizmu.
Analiza przyspieszeń mechanizmu.
Podsumowanie analizy kinematycznej mechanizmu oraz zestawienie wyników.
Analiza kinetostatyczna mechanizmu.
Założenia analizy:
Wartości sił obciążających mechanizm:
Człon drugi mechanizmu posiada: masę m2= 1 kg
Mechanizm znajduje się w polu grawitacyjnym
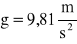
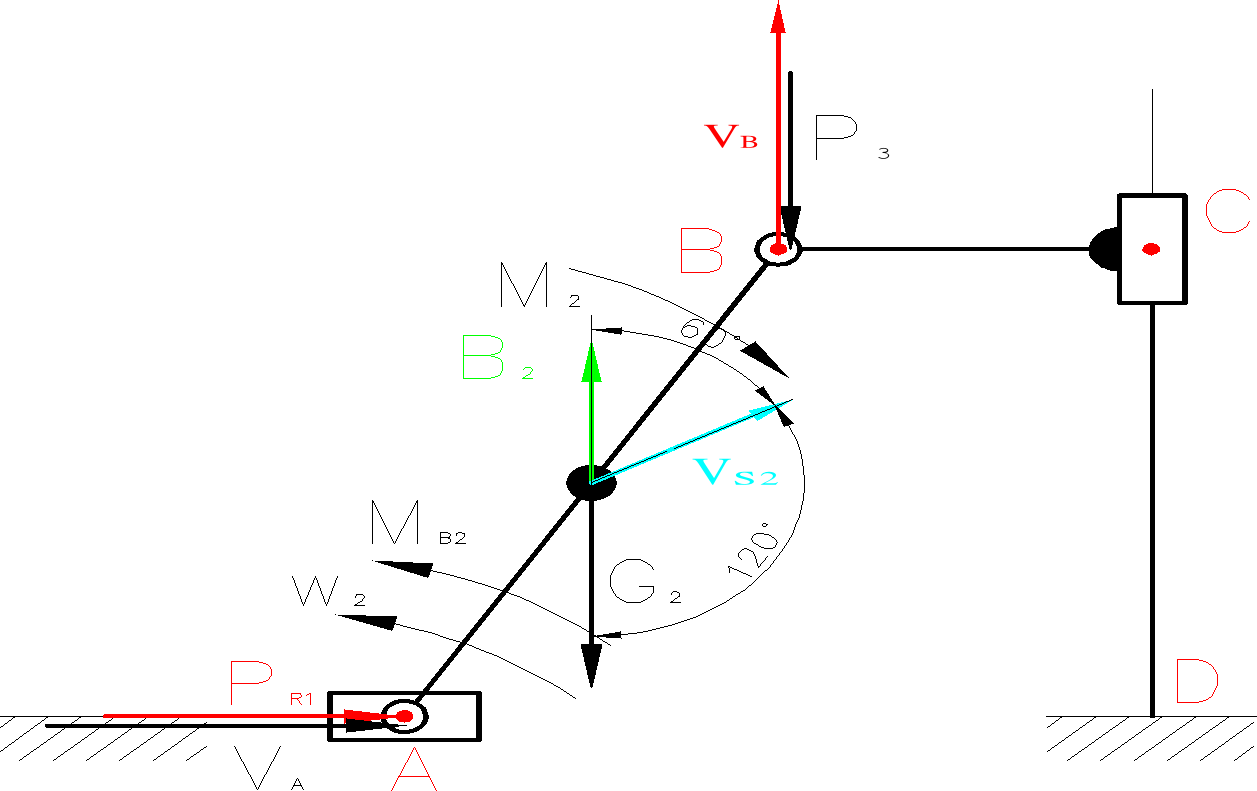
Analiza kinetostatyczna mechanizmu
Wyznaczenie sił bezwładności działających na mechanizm:
Wyznaczenie sił grawitacji działających na mechanizm:
Odrzucenie członu napędzającego, oraz uwolnienie układu od więzów
Równanie wektorowe równowagi sił działających na człon napędzający:
Wyznaczenie nieznanej reakcji R12t z równania momentów względem punktu B (równanie momentów dla członu drugiego)
Wyznaczenie pozostałych reakcji w grupie strukturalnej:
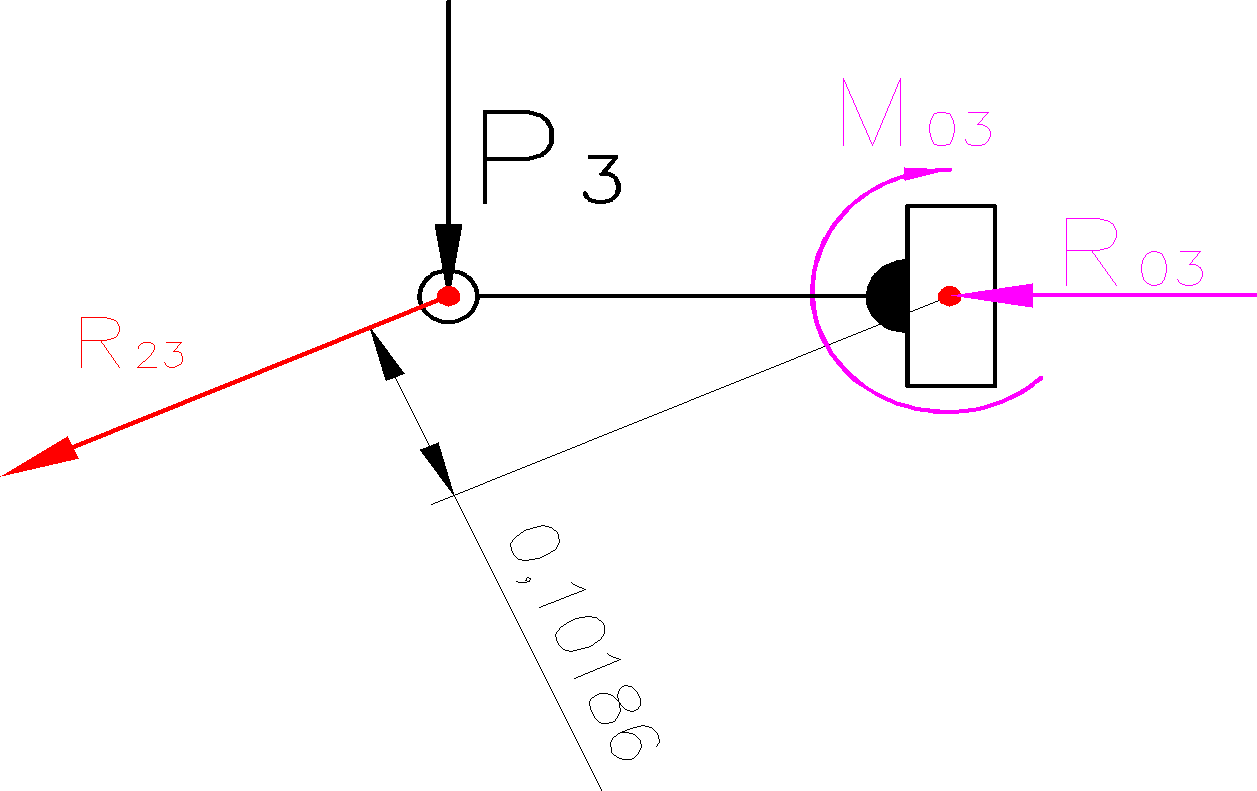
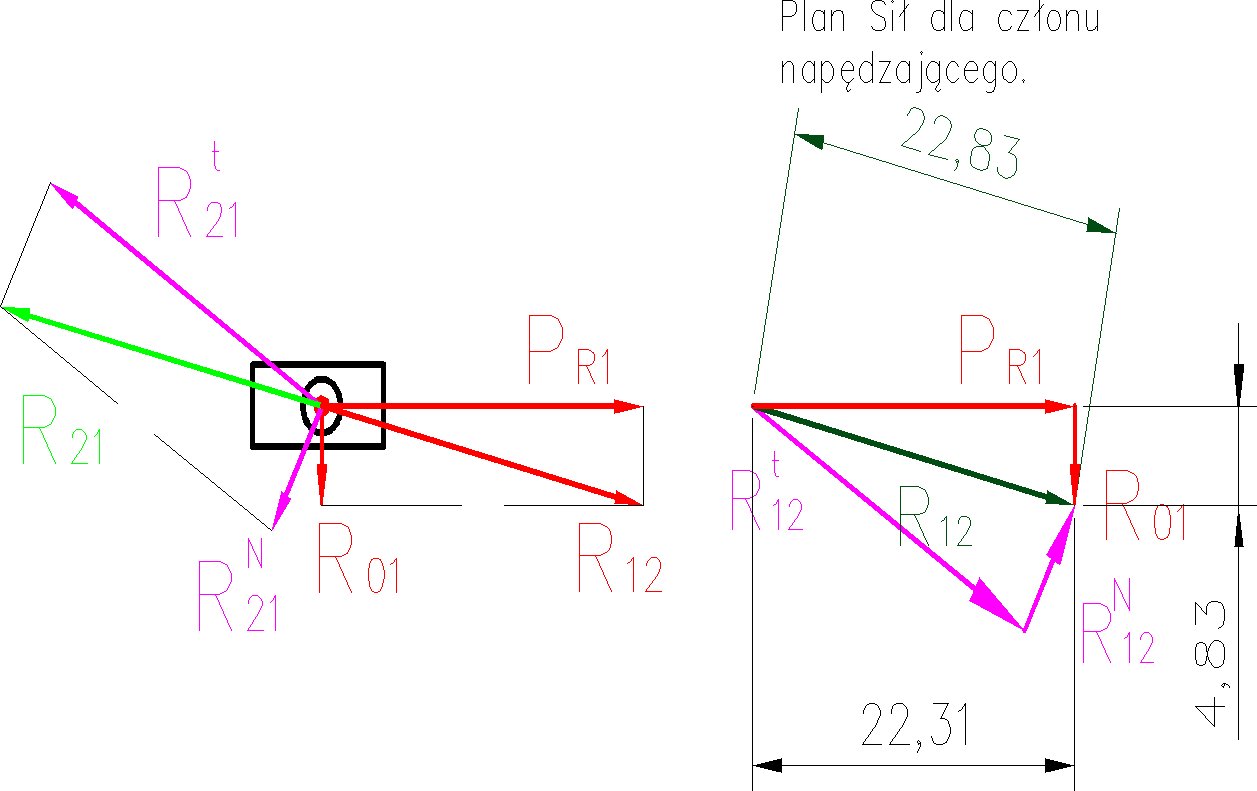
Wyznaczenie siły równoważącej działającej na człon napędzający:Z planu sił dla członu napędzającego odczytano następujące wartości:
Wyznaczenie siły równoważącej działającej na człon metoda mocy chwilowych:
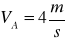
Podsumowanie analizy kinetostatycznej.
![]()
Po zrzutowaniu na osie układu wsp. otrzymujemy:
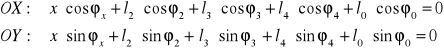
Po uwzględnieniu znanych i stałych w czasie parametrów mechanizmu otrzymujemy:
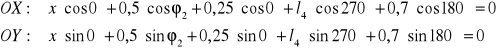

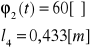
Różniczkując równania drogi po czasie otrzymamy zależność odpowiednich prędkości od czasu. Dla czasu t=0, ![]()
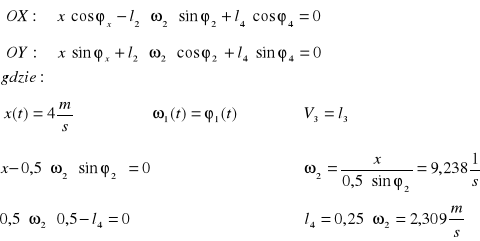

Różniczkując równanie prędkości po czasie otrzymamy zależność odpowiednich przyśpieszeń od czasu.
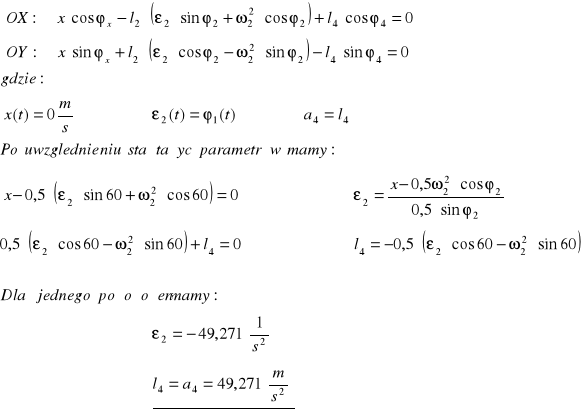
|
metoda grafoanalityczna |
metoda analityczna |
Prędkości liniowe i kątowe mechanizmu |
||
VA |
4 |
4 |
VB |
2,309 |
2,309 |
VBA |
4,619 |
- |
|
4,619 |
2,309 |
VS2 |
2,309 |
- |
ω2 |
9,238 |
9,238 |
ω3 |
0 |
0 |
Przyspieszenia liniowe i kątowe mechanizmu |
||
aA |
0 |
0 |
aB |
49,27 |
49,271 |
|
42,67 |
- |
|
24,64 |
- |
aC |
49,27 |
49,271 |
aS2 |
24,64 |
- |
ε2 |
49,28 |
-49,271 |
ε3 |
0 |
- |
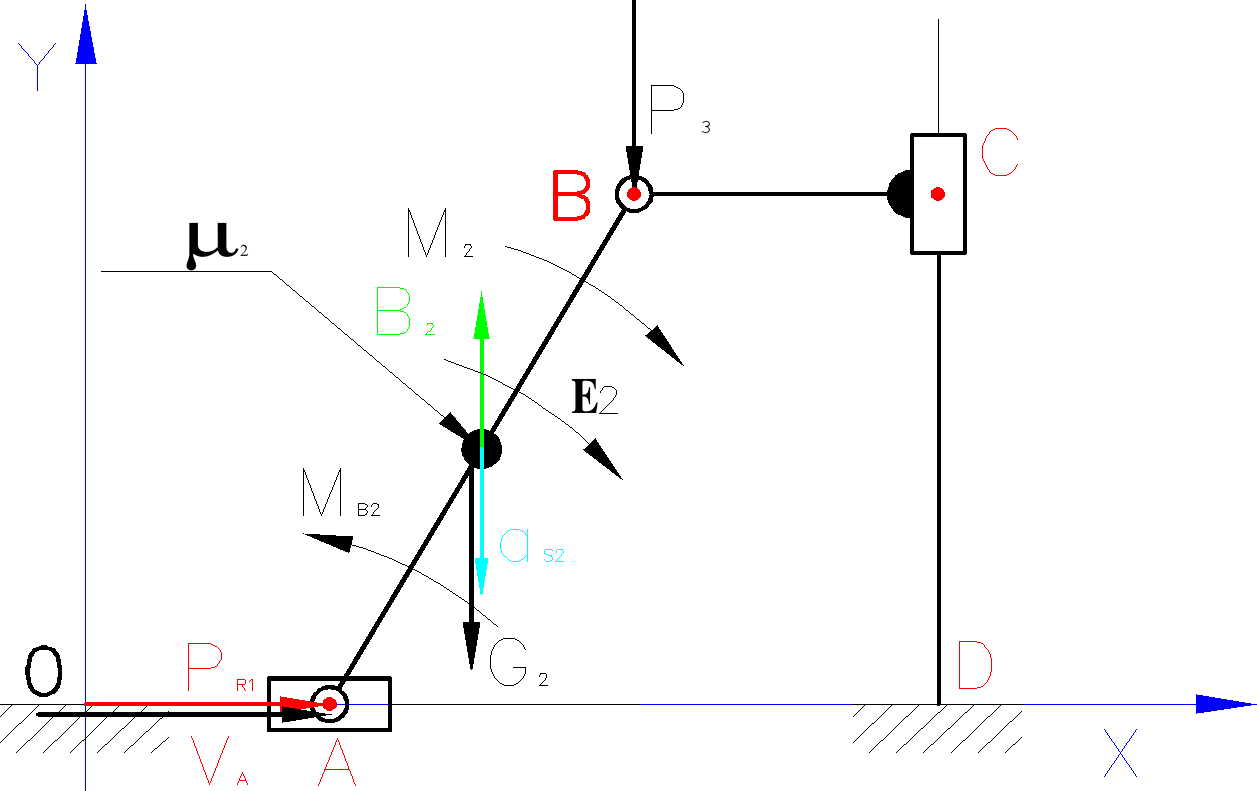
Dla mechanizmu przyjmuje:
P3=10N
M2=10Nm
moment bezwładności JS2
![]()
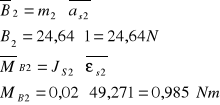
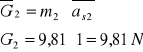

![]()
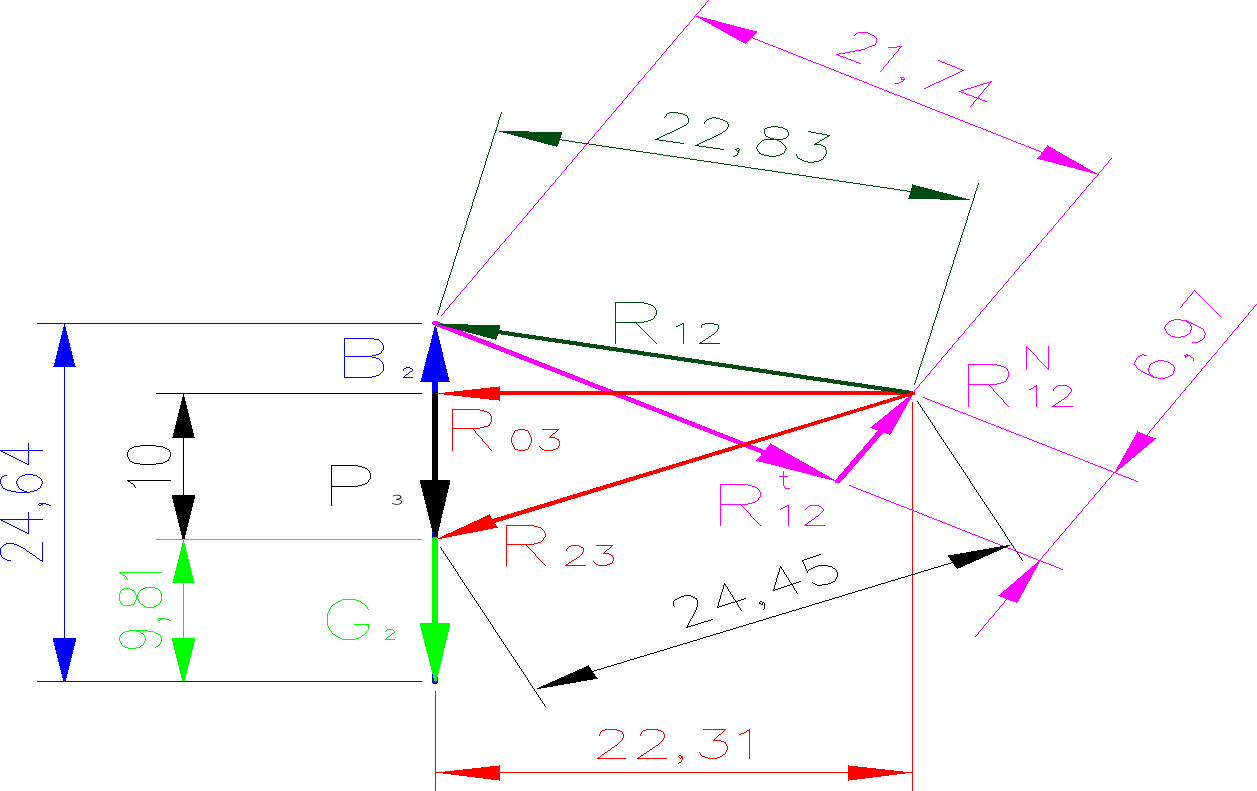
Na podstawie planu sił wyznaczono
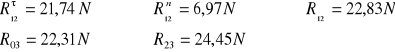
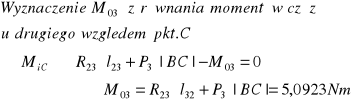
Siła równoważąca:
![]()
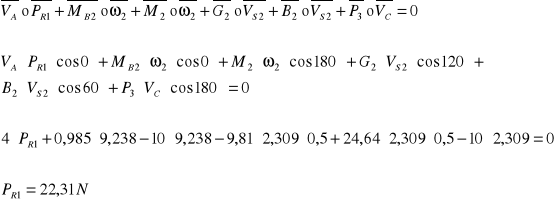
Siła równoważąca:
![]()
|
metoda wykreślna |
metoda mocy chwilowych |
PR1 |
22,31 |
22,31 |
Bartosz Hebda IMiR gr. 3 Projekt z TMM
- 11 -
φ2
φ3
φ4
φ0
φx
πV
πa
Wyszukiwarka
Podobne podstrony:
TMM+3b - zmieniony, Studia Mechatronika, Semestr 4, TMM, Projekty
TMM projekt, Studia Mechatronika, Semestr 4, TMM, Projekty
najlepsz wersja chyba, Studia Mechatronika, Semestr 4, TMM, Projekty
2B-I, Studia Mechatronika, Semestr 4, TMM, Projekty
tmm3a odz, Studia Mechatronika, Semestr 4, TMM, Projekty
5Bmoje, Studia Mechatronika, Semestr 4, TMM
TMM sprawko 1, Studia Mechatronika, Semestr 4, TMM
TI -wyklad 2, Studia - Mechatronika, I semestr, Technologia Informacyjna
Elektronika 6, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 6
Sprawko nasze, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 5
sprawko metro, Studia Mechatronika, Semestr 4, Metrologia
Elektronika 5 protokół stary, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 5
2 projekt Biedka czaro poprawiona, studia IŚ, semestr 9, Biedka, projekt 2
Pytania na kolosa, Studia, Mechatronika, Semestr III, Techniki wytwarzania i systemy montażu, Wykład
Elektronika 6 protokół nowy, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw. 6
Sprawko stabilizacja napięcia, Studia, Mechatronika, Semestr IV, Podstawy elektroniki, Laborki, ćw.
więcej podobnych podstron