POLITECHNIKA ŚLĄSKA W GLIWICACH
WYDZIAŁ MECHANICZNY-TECHNOLOGICZNY

Katedra Technologii Maszyn
i Zintegrowanych Systemów Wytwarzania
Projekt manipulatora
Piotr Tomaszewski
Gr. III
Semestr V AiR
Projekt manipulatora Piotr Tomaszewski
SPIS TREŚCI
ZAŁOŻENIA PROJEKTOWO KONSTRUKCYJNE
1.1. Opis działania 4 1.2. Dane ilościowe 4
1.3. Kryteria projektowe 5 1.4. Dobór wariantu manipulatora 5
KONCEPCJE MANIPULATORA
2.1. Wybrana koncepcja 11
2.2. Schemat gniazda robota 12
OBLICZENIA I DOBÓR NAPĘDÓW
3.1. Strzałka ugięcia ramienia manipulatora 14
3.2. Strzałka ugięcia słupa manipulatora 18
3.3. Warunek wytrzymałościowy ramienia 20
3.4. Dobór siłownika napędzającego ramię 22
3.5. Dobór siłownika napędzającego słup 24
3.6. Dobór siłownika obracającego słup 26
3.7. Dobór połączenia sworzniowego 27
3.8. Dobór łożysk 28
3.9. Obliczenie połączenia śrubowego 29
3.10. Obliczenie połączenia spawanego 33
ZAŁĄCZNIKI 40
ZAŁOŻENIA PROJEKTOWO KONSTRUKCYJNE
Opis działania
Przedmiotem manipulacji jest półfabrykat w postaci walca. Średnica d jest równa jego wysokości H. Przedmiot ten jest obrabiany na obrabiarkach o wysokościach h1 i h2. Gniazdo robocze ma średnicę podaną jako D. Z góry określona została także masa chwytaka, jak i wymiary przedmiotu obrabianego.
Manipulator wykonywać będzie następujące operacje:
uchwycenie obiektu z magazynu wejściowego,
przemieszczenie obiektu przed uchwyt samocentrujący obrabiarki 1,
wprowadzenie obiektu do uchwytu samocentrującego,
obróbka obiektu (wykonuje obrabiarka 1),
uchwycenie obrabianego przedmiotu przez manipulator,
wysunięcie przedmiotu z uchwytu,
przemieszczenie przedmiotu przed uchwyt obrabiarki 2,
wprowadzenie przedmiotu w uchwyt samocentrujący,
obróbka powierzchni (wykonuje obrabiarka 2),
uchwycenie obrabianego przedmiotu przez manipulator,
manipulacja przedmiotem,
wsunięcie obrobionego przedmiotu do odbiornika
Dane ilościowe
Przedmiot obrabiany:
H = 150 [mm]
d = 150 [mm]
tworzywo - aluminium
masa chwytaka mch = 10 [kg]
średnica gniazda D = 4 [m]
wysokość położenia uchwytów obrabiarek: h1 = 190 [mm]
h2 = 480 [mm]
Kryteria
K 1. Minimalna masa manipulatora.
K 2. Minimalna długość ruchów jałowych.
K 3. Prostota działania i wykonania manipulatora.
K 4. Błąd pozycjonowania od 0.2 do 0.4 [mm].
K 5. Estetyka wykonania manipulatora.
K 6. Maksymalny stopień wykorzystania elementów znormalizowanych.
Dobór wariantu manipulatora
-- |
K 1 |
K 2 |
K 3 |
K 4 |
K 5 |
K 6 |
ΣKi |
W 1 |
W 2 |
W 3 |
W4 |
W5 |
Wid |
K 1 |
-- |
0,5 |
0 |
0 |
0,5 |
0 |
1 |
3 |
4 |
3 |
3 |
3 |
5 |
K 2 |
0,5 |
-- |
0 |
0.5 |
1 |
0,5 |
1,5 |
3 |
4 |
3 |
5 |
4 |
5 |
K 3 |
1 |
1 |
-- |
0 |
1 |
0,5 |
3,5 |
4 |
4 |
3 |
4 |
3 |
5 |
K 4 |
1 |
0.5 |
1 |
-- |
1 |
0,5 |
4 |
4 |
5 |
3 |
3 |
3 |
5 |
K 5 |
0,5 |
0 |
0 |
0 |
-- |
0 |
0,5 |
4 |
5 |
4 |
4 |
5 |
5 |
K 6 |
1 |
0,5 |
0,5 |
0,5 |
1 |
-- |
3,5 |
4 |
5 |
3 |
3 |
4 |
5 |
![]()
P1 |
P2 |
P3 |
P4 |
P5 |
Pid |
53,5 |
64 |
42 |
49 |
48 |
70 |
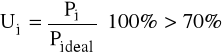
U1 |
U2 |
U3 |
U4 |
U5 |
% |
% |
% |
% |
% |
76,4 |
91,4 |
60 |
70 |
68 |
Wybieram drugi wariant manipulatora
OBLICZENIA
Strzałka ugięcia ramienia manipulatora
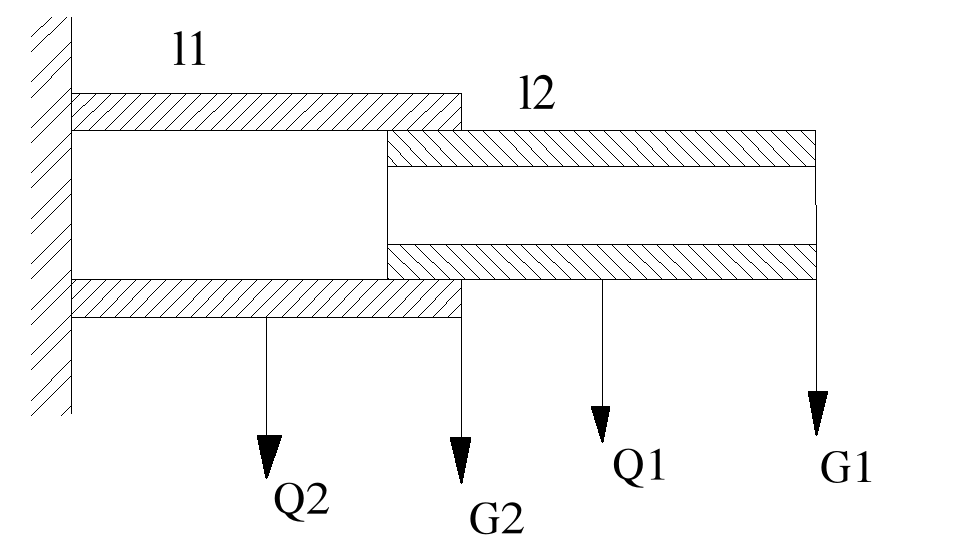
Całkowita strzałka ugięcia ramienia robota jest sumą strzałki ugięcia ramion l1 i l2.
Strzałka ugięcia ramienia l1 składa się z sumy strzałek ugięcia pochodzących od sił G1 i Q1.
Siła G1 składa się z dwóch sił; siły pochodzącej od masy chwytaka i masy przedmiotu.
G1 = ( mch + mp ) ⋅ g
mch - masa chwytaka wynosi 10 [ kg ]
mp. - masa przedmiotu w postaci walca wykonanego z aluminium o
wymiarach:
h = 150 [ mm ]
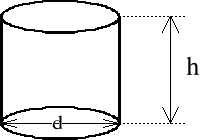
d = 150 [ mm ]
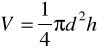
Objętość walca otrzymamy ze wzoru:
![]()
V = 0.0026 [ m3 ]
Gęstość aluminium wynosi ρAl. = 2700 [ kg / m3 ]
Masa przedmiotu wyraża się wzorem:
mp = V⋅ρ = 9,72 [ kg ]
G1 = ( 10 + 9,72 ) ⋅ 9,81 = 193,45 [ N ]
Siła Q1 jest siłą pochodzącą od obciążenia ciągłego ramienia l1
Q1 = l1 ⋅ q1 ⋅ g
gdzie:
q1 - masa obciążenia ciągłego ramienia 1
l1 - długość ramienia 1
g - przyspieszenie ziemskie
Ramię l1 będzie wykonane z kształtownika zamkniętego kwadratowego według BN - 79 / 0656 - 01 o wymiarach 90×90×3, masie ciągłej
q1 = 7.88 [ kg / m. ], momencie bezwładności I1 = 124.8 [ cm4 ] i długości l1 = 1.2 [ m. ].
Q1 = 92.8 [ N ]
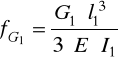
Strzałka ugięcia ramienia robota pochodząca od siły G1
moduł Younga dla stali E = 2.1⋅1011 [ N / m2 ]
fG1 = 4,24⋅ 10- 5 [ m ]
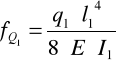
Strzałka ugięcia ramienia robota pochodząca od siły Q1
fQ1 = 7.77⋅10-7 [ m ]
Strzałka ugięcia ramienia l1
fl1 = fG1 + fQ1
fl1 = 4,31 ⋅ 10 -5 [ m ]
Strzałka ugięcia ramienia l2 składa się z sumy strzałek ugięcia pochodzących od sił G2 i Q2.
Siła G2 jest sumą sił G1 i Q1.
G2 = G1 + Q1
G2 = 286,21 [ N ]
Siła Q2 jest siłą pochodzącą od obciążenia ciągłego ramienia l2.
Q2 = l2⋅q2⋅g
gdzie:
q2 - masa obciążenia ciągłego ramienia 2
l2 - długość ramienia 2
g - przyspieszenie ziemskie
Ramię l2 będzie wykonane z kształtownika zamkniętego kwadratowego według BN - 79 / 0656 - 01 o wymiarach 100×100×3, masie ciągłej
q2 = 8.82 [ kg / m. ], momencie bezwładności I2 = 173.9 [ cm4 ] i długości l2 = 1.4 [ m ].
Q2 = 121.1 [ N ]
Strzałka ugięcia ramienia robota pochodząca od siły G2
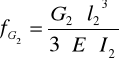
fG2 = 7,15⋅ 10-5 [ m ]
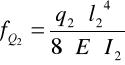
Strzałka ugięcia ramienia robota pochodząca od siły Q2
fQ2 = 1,15 ⋅ 10-6 [ m ]
Strzałka ugięcia ramienia l2
fl2 = fG2 + fQ2
fl2 = 7,26 ⋅ 10 -5 [ m ]
Całkowita strzałka ugięcia ramienia robota
fr = fl1 + fl2
fr = 1,15⋅10-4 [ m ] = 0,15 [ mm ]
3.2. Strzałka ugięcia słupa manipulatora.
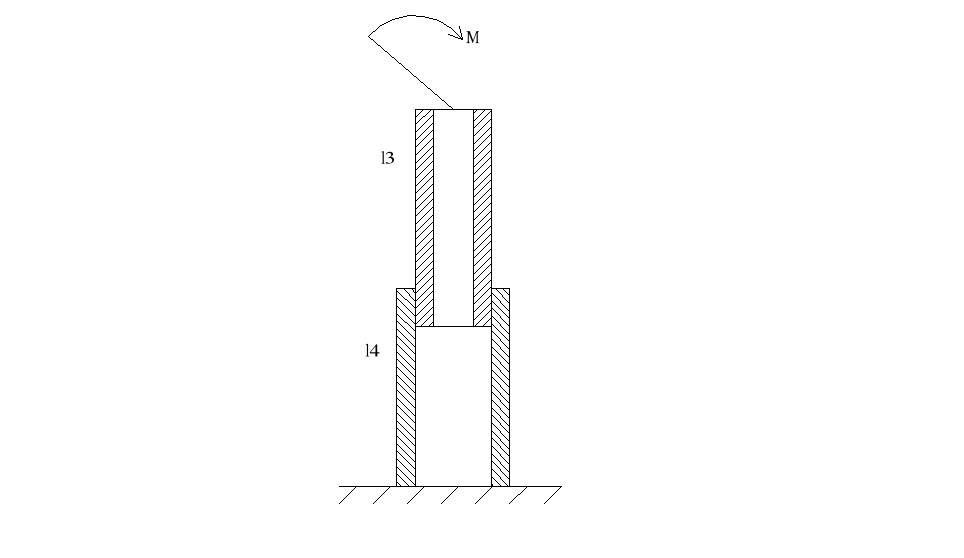
Całkowita strzałka ugięcia słupa manipulatora jest sumą strzałki ugięcia ramienia l3 i l4.. Strzałka ugięcia ramienia l3 wywołana jest momentem gnącym Mg.
Moment gnący M składa się z momentów gnących działających na słup pochodzących od ramienia robota i wynosi.
Mg = G2⋅l2 + Q2⋅l2
Mg = 570,22 [ Nm ]
Ramię l3 będzie wykonane z kształtownika zamkniętego kwadratowego według BN - 79 / 0656 - 01 o wymiarach 90×90×3, masie ciągłej
q3 = 7.88 [ kg / m. ], momencie bezwładności I3 = 124.8 [ cm4 ] i długości l3 = 0.8 [ m ].
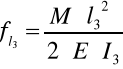
Zatem strzałka ugięcia ramienia l3
moduł Younga dla stali E = 2.1⋅1011 [ N / m2 ]
fl3 = 6,94 ⋅ 10 -5 [ m ]
Strzałka ugięcia ramienia l4 wywołana jest także momentem gnącym M.
Ramię l4 będzie wykonane z kształtownika zamkniętego kwadratowego według BN - 79 / 0656 - 01 o wymiarach 100×100×3, masie ciągłej
q4 = 8.82 [ kg / m. ], momencie bezwładności I4 = 173.9 [ cm4 ] i długości l4 = 1,0 [ m ].
Zatem strzałka ugięcia ramienia l4
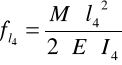
fl4 = 7,78⋅10-5 [ m ]
Całkowita strzałka ugięcia słupa robota
fs = fl3 + fl4
fs = 1,47 ⋅ 10 -4 [ m ] = 0,14 [ mm ]
3.3. Warunek wytrzymałościowy ramienia
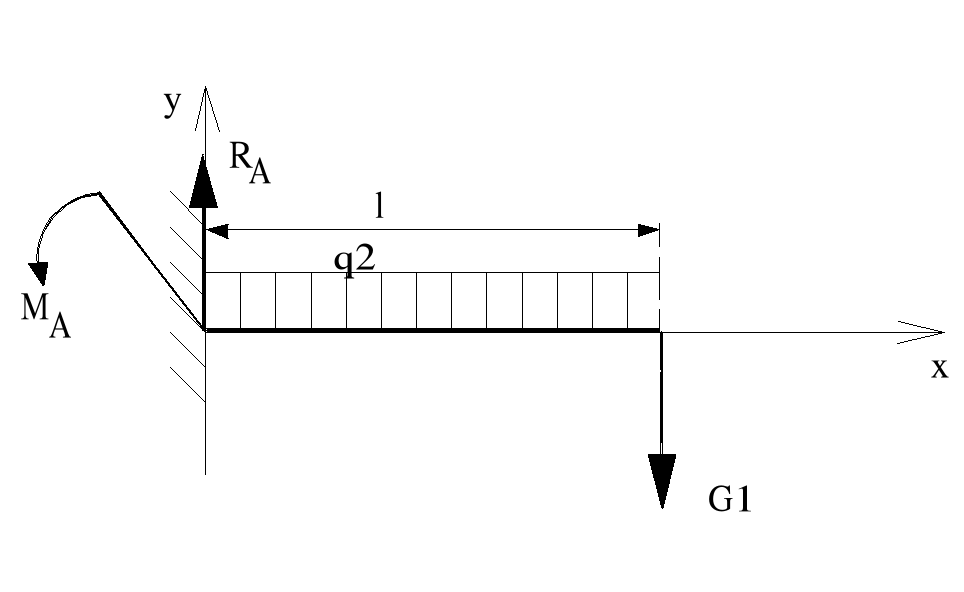
Dane:
l = l1 + l2 = 2.6 [ m. ]
G1 = 193,45 [ N ]
q2 = 8.82 [ kg / m. ] = 86.5 [ N / m. ]
ΣFix = 0
ΣFiy = RA - q2 ⋅ l - G1
RA = 86,5⋅ 2,6 + 193,45
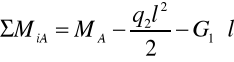
RA = 418,3 [N]
MA = ˝⋅ (86,5 ⋅ 2,62) + 193,45 ⋅ 2,6
MA = 795,3 [ Nm ]
Maksymalny moment gnący
Mg max = MA = 795,3 [ Nm ]
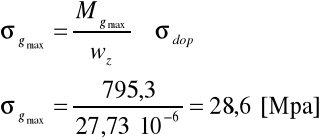
Warunek wytrzymałościowy
σdop - naprężenie dopuszczalne na zginanie
wz - wskaźnik wytrzymałości na zginanie dobrano z norm
wz = 27.73⋅10-6 [ m3 ]
σdop dla stali ST3S wynosi około 100 [ Mpa ]
28,6 [ Mpa ] ≤ 100 [ Mpa ]
Ponieważ powyższa nierówność jest spełniona kształtownik został dobrany prawidłowo.
Dobór siłownika napędzającego ramię
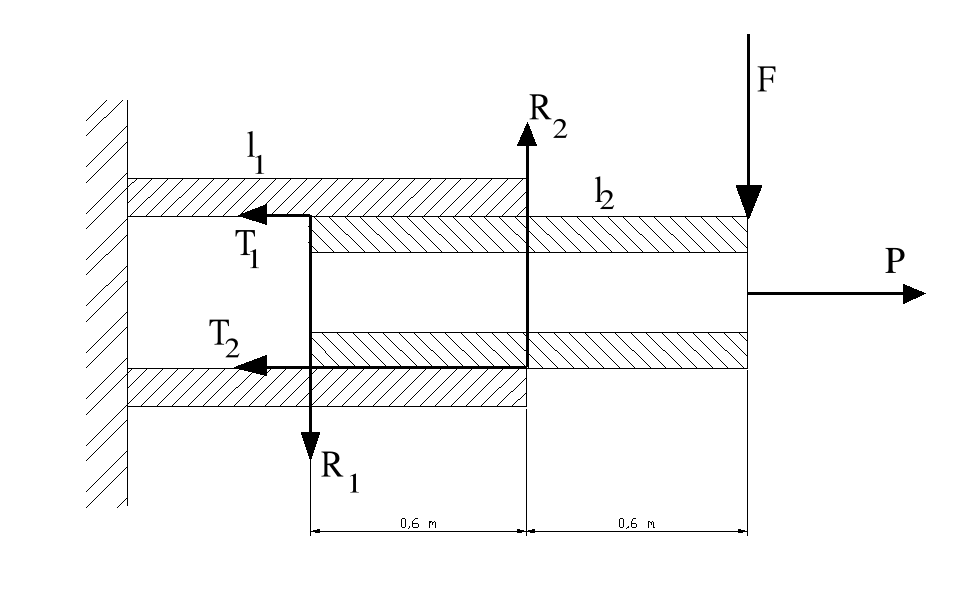
Siła P napędzająca ramię musi być większa od sił tarć T1 i T2 występujących na górnej i dolnej ściance.
Aby obliczyć te siły należy wyznaczyć siły reakcji R1 i R2.
Wyznacza się je z równania sumy rzutów sił na oś pionową „ y ” oraz z równania sumy momentów względem punktu 0.
Siłę F przyjmuje się jako sumę sił G1 i Q1; (siły pochodzącej od masy chwytaka i masy przedmiotu obrabianego ) i (siły pochodzącej od masy obciążenia ciągłego ramienia l1 ).
ΣFiy = - F - R1 + R2 = 0
ΣMio = R2⋅0.6 - F⋅1.2 = 0
R1 = R2 - F
R2 = 2 F
R1 = F
R1 = 286,2 [ N ]
R2 = 572,4 [ N ]
Siła tarcia T jest iloczynem siły reakcji R i współczynnika tarcia posuwistego μ ( dla stali μ = 0.3 )
T1 = R1 ⋅ μ T2 = R2 ⋅ μ
T1 = 82.29 [ N ] T2 = 171,7 [ N ]
Siła P musi być większa od sumy sił tarć T1 i T2 więc:
P > T1 + T2
P > 246.8 [ N ]
powinna być ona większa od wartości podanej powyżej.
Dobieram siłownik:
FESTO PNEUMATIC LINEAR DRIVER DSNU-25-500PPV-A
o sile 294,5 N
3.5. Dobór siłownika napędzającego słup.
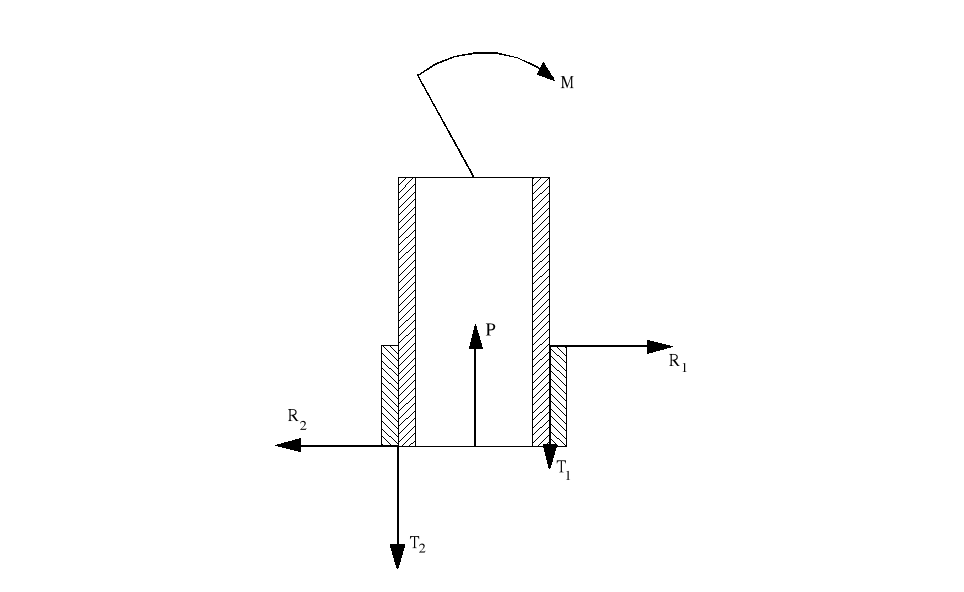
Siła P napędzająca słup musi być większa od siły tarć T1 i T2 występujących na bocznych ściankach. Aby obliczyć te siły należy wyznaczyć siły reakcji R1 i R2. Wyznacza się je z równania sumy rzutów sił na oś poziomą „ x ” oraz z równania sumy momentów względem punktu 0.
ΣFix = R1 - R2 = 0
ΣMio = R2⋅0.3 - M = 0
R1 = R2
R2 = M / 0.3
R1 = R2
R1 = 2651 [ N ]
R2 = 2651 [ N ]
Siła tarcia T jest iloczynem siły reakcji R i współczynnika tarcia posuwistego μ = 0.3
T1 = R1 ⋅ μ T2 = R2 ⋅ μ
T1 = 795 [ N ] T2 = 795 [ N ]
Siła P musi być większa od sumy sił tarć T1 i T2, co daje nam:
P > T1 + T2
P > 1590 [ N ]
powinna być ona większa od wartości podanej wyżej.
Dobieram siłownik:
FESTO PNEUMATIC LINEAR DRIVER DNC-63-500PPV-A
o sile 1870 N
3.6. Dobór siłownika obracającego słup nośny --> [Author:AM]
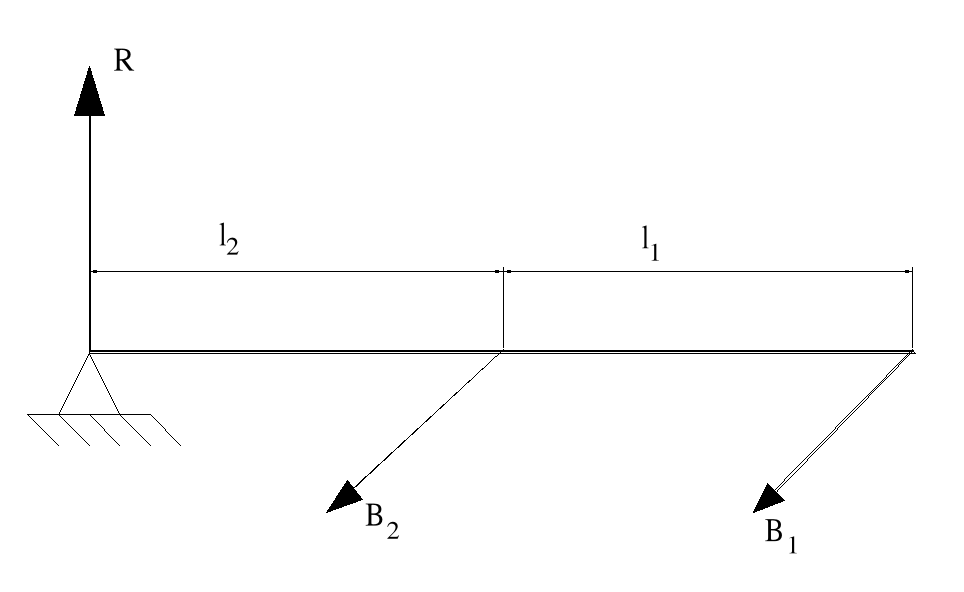
α = 1.25 współczynnik wyrównawczy
l1 = 1.2 [ m. ]
l2 = 1.4 [ m. ]
m1 = q1⋅l1 = 7.88 ⋅ 1.2 = 9.5 [ kg ]
m2 = q2⋅l2 = 8.82 ⋅ 1.4 = 12.4 [ kg ]
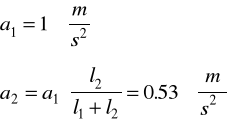
B1 = α⋅m1⋅a1 = 11.8 [ N ]
B2 = α⋅m2⋅a2 = 8.2 [ N ]
M = B1⋅l1 + B2⋅l2 = 25.64 [ Nm ]
Mzn = M ⋅ 0.2 = 5.2 [ Nm ]
Dobieram siłownik:
FESTO PNEUMATIC CYLINDRICAL DRIVER DSM-40-270-FW-CR
o sile 20 Nm
3.7. Dobór połączenia sworzniowego
Siłownik połączony jest poprzez ucho i sworzeń z ramieniem manipula-tora. Ponieważ sworzeń jest pasowany oblicza się go z warunku na ścinanie. Sworzeń wykonany jest ze stali St 5, dla której:
ks = 90 [ Mpa ]
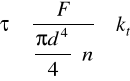
a skoro ks ≈ kt
Największą siłą powodującą ścinanie sworznia przy połączeniu z ramieniem bądź słupem robota jest siła napędzająca słup ustroju nośnego, czyli
F = 1770 [ N ]
n = 1
kt = 90 [ Mpa ]
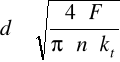
Z warunków wytrzymałościowych oblicza się średnicę sworznia
d ≥ 0.0074 [ m ]
PRZYJMUJĘ ŚREDNICĘ SWORZNIA d = 12 mm
3.8. Dobór łożysk
Łożyska dobieram na podstawie danych ilościowych:
Średnica wałka dla łożyska oporowego = 150 mm
Dobieram łożysko kulkowe zwykłe nr 16030 o wymiarach:
D = 250 mm
d = 150 mm
Średnica wałka dla łożyska oporowo-nośnego = 150 mm
Dobieram łożysko baryłkowe wzdłużne nr 29330 o wymiarach:
D = 250 mm
d = 150 mm
gdzie:
D - średnica zewnętrzna łożyska
d - średnica wewnętrzna łożyska
3.9. Obliczenie połączenia śrubowego
Obliczenie połączenia śrubowego dotyczyć będzie czterech śrub mocujących robota do sufitu.
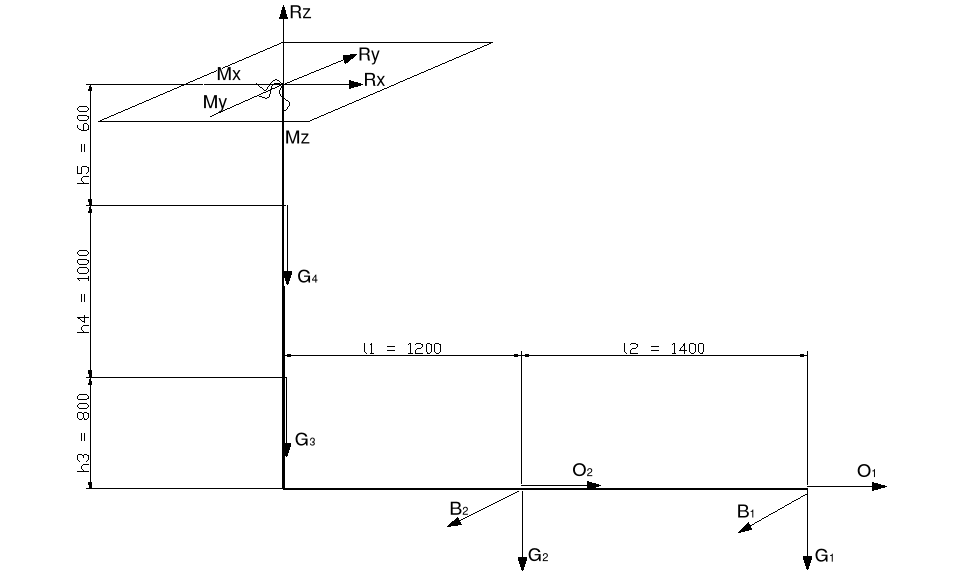
Siły ciężkości:
G1 = 193,45 [N]
G2 = 286,21 [N]
G3 = 61,81 [N]
G4 = 86,52 [N]
Przyspieszenia :
a1 = 1 [m/s2]
a2 = 0,53 [m/s2]
Siły bezwładności
B1 = m1a1 = 193,45 [N]
B2 = m2a2 = 286,21 [N]
Siły odśrodkowe:
v1 = a1t = 2 [m/s] dla t = 2 [s]
v2 = a2t = 1,06 [m/s]
Siły odśrodkowe poszczególnych punktów
O1 = m1 (v12 / l1 ) = 25,2 [N]
O2 = m2 (v22 / l2 ) = 8,84 [N]
Obliczam śruby metodą naciskową
Siły i momenty w złączu:
Rx = O1 + O2 = 44 [N]
Ry = -B1 - B2 = -20 [N]
Rz = -G1 - G2 - G3 = -628 [N]
Mx = -B1h - B2h = -51,3 [Nm]
My = -O1h - O2h + G1l + G2l = 1133 [Nm]
Mz = -B2l2 - B1l1 = -25,6 [Nm]
Płyta mocująca manipulator:
y
x
a as
as
a
a = 180 [cm] as = 150 [cm]
Nacisk wywołani siłami napięcia wstępnego:
![]()
gdzie: z = 4 - ilość śrub
Powierzchnia Fst styku blachy z podłożem wynosi:
Fst = a2 = 3,24 [m2]
Naciski od sił ciężkości i momentów gnących:
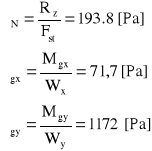
Wartość wypadkowa nacisku:
![]()
Uwzględniając warunek wytrzymałościowy:
![]()
otrzymamy:
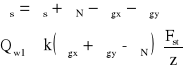
gdzie k = 1.5 - liczba bezpieczeństwa
Qw1 = 1746 [N]
Drugi warunek wynika z rozpatrzenia sił próbujących przesunąć płytę po podłożu i sił tarcia wywołanych przez nacisk śrub na podłoże. Przy uwzględnieniu k=1.5 otrzymamy:
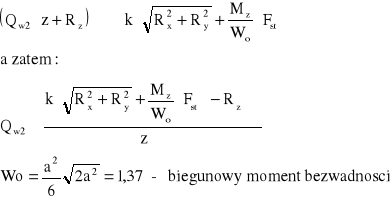
Qw2 = 293,1 [N]
Do dalszych obliczeń przyjmuję większą z dwóch wartości w rdzeniu śruby:
Qw = max [ Qw1, Qw2 ] = 293,1 [N]
Obliczenie rdzenia śruby:
Opierając się na warunku wytrzymałościowym:
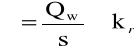
oraz tym, że powierzchnia s ze wzoru powyższego dana jest wzorem:
![]()
zapisujemy minimalną średnicę rdzenia:
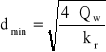
Naprężenie dopuszczalne oblicza się na podstawie granicy plastyczności dla materiału śruby Re = 180 Mpa ( dla śrub klasy 3.6 wg. PN/M-85061) i przyjmując współczynnik bezpieczeństwa x = 2 mamy:
kr=90 Mpa
otrzymamy minimalną średnicę śruby:
d min = 5,12 [ mm ]
Na tej podstawie dobieram cztery śruby M10
3.10. Obliczenie połączenia spawanego
Obliczenie połączenia spawanego dotyczyć będzie spoiny czołowej mocującej obudowę robota do płyty nośnej.
Masy poszczególnych elementów (z dokładnością + 10 %)
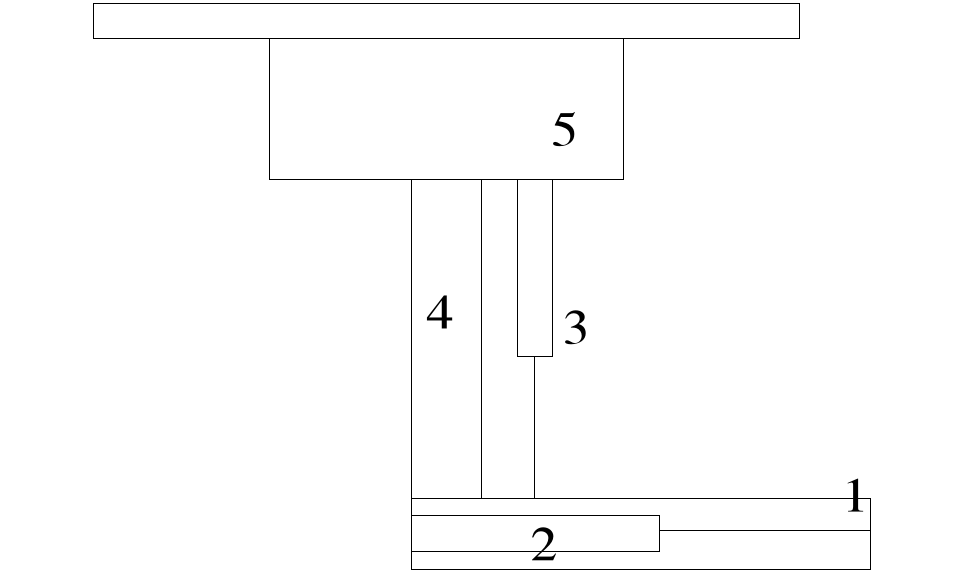
m1 = 22 [kg]
m2 = 12 [kg]
m3 = 22 [kg]
m4 = 15 [kg]
m5 = 50 [kg]
przyjmuję współczynnik wyrównawczy = 1.25
Siły ciężkości:
G1 = m1g = 270 [N]
G2 = m2g = 147 [N]
G3 = m3g = 270 [N]
G4 = m4g = 184 [N]
G5 = m5g = 613 [N]
Przyspieszenia:
a1 = 1 [m/s2]
a2 = 0,53 [m/s2]
a3 = 0,14 [m/s2]
Siły bezwładności
B1 = m1a1 = 27,5 [N]
B2 = m2a2 = 8,5 [N]
B3 = m3a3 = 3,8 [N]
Siły odśrodkowe:
v1 = a1t = 2 [m/s]
v2 = a2t = 1,14 [m/s2] dla t = 2 [s]
v3 = a2t = 0,28 [m/s2]
Siły odśrodkowe poszczególnych mas
O1 = m1 (v12 / l1 ) = 42,3 [N]
O2 = m2 (v22 / l2 ) = 16,2 [N]
O3 = m3 (v32 / l3 ) = 9,62 [N]
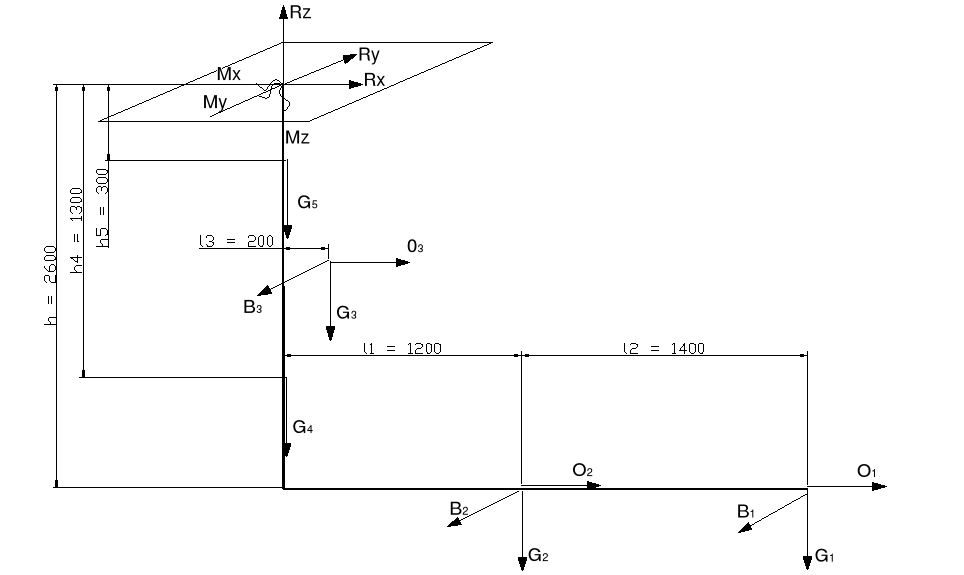
Siły i momenty w spoinie:
Rx = O1 + O2 + O3 = 68,1 [N]
Ry = -B1 - B2 - B3 = -39,8 [N]
Rz = -G1 - G2 - G3 - G4 - G5 = -1500 [N]
Mx = -B1h1 - B2h2 - B3h3 = -97 [Nm]
My = -O3 h3 - (O2 + O1)h + G3 h3 + (G2 + G1)h = 1166 [Nm]
Mz = -B3h3 - (B1 + B2) h = 97 [Nm]
y
b = 1300
X
g = 5 a = 1300
B = b + 2 g
H = a + 2 g
Momenty bezwładności przekroju:
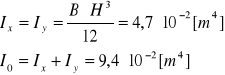
Wskaźniki wytrzymałościowe:
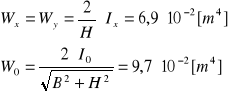
Naprężenia w spoinie wywołane siłami i momentam
Dla i spoiny czołowej trzeba określić naprężenia dopuszczalne. Zgodnie z normą PN/B 03200 dla spoiny czołowej ss = 0.6 w przypadku ścinania oraz sn = 1 dla naprężeń normalnych. Naprężenia muszą spełniać następujące warunki:
![]()
![]()
Pole przekroju spoiny:
P = BH = 0,15 [m2]
Poszczególne naprężenia w złączu spawanym wynoszą:
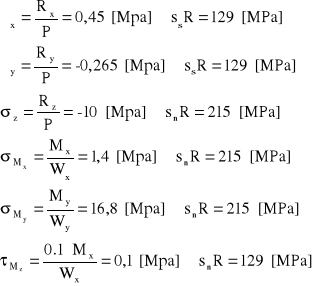
Weryfikacja najbardziej obciążonego miejsca spoiny
σz
y
x
Mz
σMy
σMx
A
Najbardziej obciążonym punktem spoiny jest punkt A i dla niego przeprowadzone zostaną dalsze obliczenia
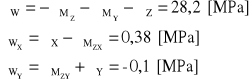
Zatem wypadkowe naprężenie styczne przyjmie postać:
![]()
Zgodnie z normą PN/B-03200 wypadkowe naprężenie normalne musi spełniać następujący warunek:
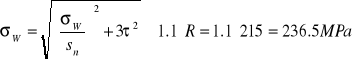
Ponieważ σW = σA
σ = 28.2 [Mpa] < σW = 236.5 [Mpa]
Przedstawione sprawdzenie warunku w sposób jednoznaczny wykazuje, że warunek został spełniony.
Dobrane złącze czołowe o grubości 5 mm jest wystarczające
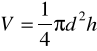
![]()
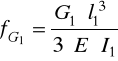
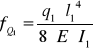
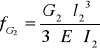
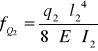
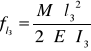
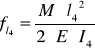
![]()
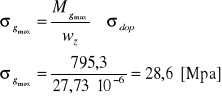
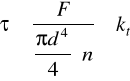
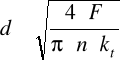
Wyszukiwarka
Podobne podstrony:
Projekt manipulatora, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, A PROJEKT MANIPULA
Konstruowanie katalogowe manipulatorów, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty,
Manipulator, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty
Projekt pkm2, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa
pkm, Automatyka i Robotyka, Semestr 5, PKM, projekty
pstan, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa, Manip
man r2, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa, Mani
man r3, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa, Mani
Pytania z PKM, Automatyka i Robotyka, Semestr 5, PKM, pytania
obliczenia do robota, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatoró
Kinematyka odwrotna, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów
Notacja Denavita, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów, p
POLITECHNIKA ŚLĄSKA W GLIWICACH fffffff, Automatyka i Robotyka, Semestr IV, Podstawy Konstrukcji mas
projekt dla rudego, Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji maszyn, Projekt
interpolacja projekt, Automatyka i Robotyka, Semestr 1, Podstawy Sterowania, projekt1-Interpolacja
Analiza cyklogramu szeregowego, Automatyka i Robotyka, Semestr 2, Robotyzacja, projekt, projekt 2
interpolacje projekt2, Automatyka i Robotyka, Semestr 1, Podstawy Sterowania, projekt1-Interpolacja
więcej podobnych podstron