OBLICZANIE BŁĘDÓW BEZPOŚREDNICH POMIARÓW JEDNOKROTNYCH

1. Wprowadzenie

Wynik pomiaru przedstawia wartość jedynie wtedy, gdy można podać stopień jego wiarygodności, tzn. przedział niepewności określany przez błąd pomiaru. Najczęściej wykonywane są jednokrotne pomiary bezpośrednie, tzn. takie, w których obiekt badany jest skojarzony z jednym przyrządem pomiarowym, bezpośrednio przystosowanym do pomiaru wartości danej wielkości, a zatem wyniki uzyskuje się bezpośrednio z urządzenia odczytowego tego przyrządu.

Błąd bezpośredniego pomiaru jednokrotnego zależy od wielu czynników, lecz przede wszystkim wynika on z błędów użytego przyrządu pomiarowego. W pierwszym przybliżeniu można przyjąć, że błąd rezultatu pomiaru jednokrotnego jest równy błędowi, którym w danym punkcie zakresu pomiarowego, charakteryzuje się użyty przyrząd pomiarowy.

Szacowanie błędów pomiaru odbywa się na podstawie wzorów właściwych dla poszczególnych typów przyrządów pomiarowych, z uwzględnieniem ich klasy dokładności, zawartej w świadectwie uwierzytelniania lub świadectwie legalizacji. Przy czym, oblicza się zarówno błąd bezwzględny Δ jak i błąd względny γ. Pierwszy z nich jest nieodzowny dla prawidłowego zaokrąglenia wyniku pomiaru i jego prawidłowego zapisu, drugi zaś w celu jednoznacznego i porównywalnego scharakteryzowania dokładności tego wyniku.

Poszczególne narzędzia pomiarowe (czujniki, przetworniki, przyrządy) charakteryzują się błędami, których natura może być różna. Jedne z nich mają praktycznie błędy
o charakterze addytywnym zwane również błędami zera. Inne - błędy multiplikatywne - zwane również błędami czułości. W jeszcze innej grupie przyrządów błąd, wzdłuż skali przyrządu, posiada bardziej złożony charakter, np. addytywno-multiplikatywny. Aby umożliwić użytkownikowi orientację w zakresie metrologicznych możliwości narzędzia pomiarowego i wcześniejszą ( a priori) ocenę błędu, który wniesie ono w końcowy wynik pomiaru, błędy narzędzi podlegają normalizacji.

Pod pojęciem błędów znormalizowanych (unormowanych) rozumie się błędy graniczne (maksymalne) dla danego typu narzędzia pomiarowego. Przy czym błędy poszczególnych egzemplarzy narzędzi tego samego typu mogą różnić się tak co do składowej systematycznej jak i składowej przypadkowej, jednakże dla danego typu narzędzia, wartość błędu nie przekracza gwarantowanej wartości. Normalizacji podlega zarówno składowa multiplikatywna jak też składowa addytywna błędu i w dokumencie towarzyszącym każdemu egzemplarzowi narzędzia pomiarowego te granice błędu podstawowego są zamieszczane.

Błąd podstawowy narzędzi pomiarowych, w zależności od wielkości mierzonej X (wzdłuż skali), określany jest na różne sposoby, o wyborze których decyduje głównie charakter związku (obszar zajmowany przez punkty X_i, Y_i) między wielkościami X i Y, ustalony podczas skalowania (kalibracji) narzędzia pomiarowego. Wielokrotnie wyznaczone charakterystyki pojedynczego narzędzia pomiarowego, lub grupy narzędzi tego samego typu, zajmują na wykresie pewien obszar. Pewna ściśle określona linia w tym obszarze jest przyjmowana za charakterystykę znamionową narzędzia danego typu jest zamieszczana
w dokumentacji i wykorzystywana w celu określenia wyniku pomiaru.

W zależności od przyjętego sposobu normalizacji błędów narzędzia pomiarowego, postępowanie, przy obliczaniu błędu pomiaru tym przyrządem jest różne.

2. Szacowanie błędów przy normalizacji addytywnej

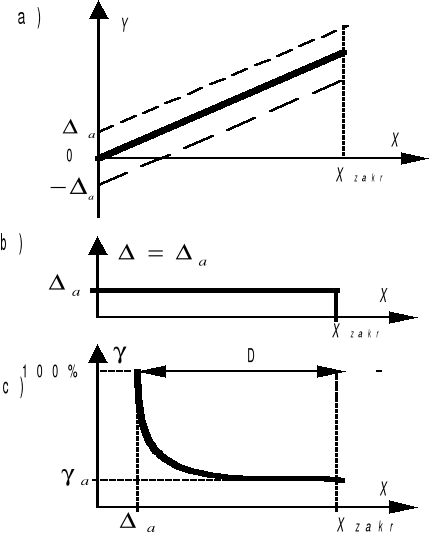
Przy normalizacji addytywnej punkty kalibracyjne (a więc i charakterystyka statyczna) układają się wewnątrz obszaru ograniczonego przez dwie proste równolegle (rys.1a). Błąd bezwzględny Δ_a pozostaje niezmienny wzdłuż skali przyrządu (rys.1b). Jednak normalizowanie błędu bezwzględnego jest w tym przypadku niewygodne i niecelowe ponieważ dla przyrządów wielozakresowych wartość Δ_a jest różna dla każdego
z podzakresów i w dokumencie towarzyszącym przyrządowi należałoby przytaczać wszystkie te wartości, dla każdego z podzakresów.

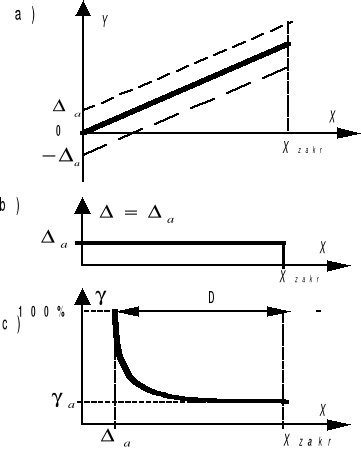
Rys.1. Ilustracja normalizacji addytywnej

Dlatego też normalizuje się nie wartości błędu bezwzględnego Δ_a a wyrażoną w procentach, sprowadzoną wartość tego błędu γ_a, odniesioną do zakresu X_zakr, tzn.:

(1)

Wartość γ_a wykorzystuje się do oznaczenia klasy dokładności tego typu przyrządów pomiarowych. Klasa, podawana za pomocą liczby należącej do szeregu: 0,05; 0,1; 0,2; 0,5; 1; 1,5; 2,5; 5, jest umieszczana na skali przyrządu i w towarzyszącej mu dokumentacji.

Bezwzględny błąd pomiaru Δ (w jednostkach wielkości mierzonej), dokonanego przyrządem o normalizacji addytywnej, jest obliczany z wzoru (2):

, (2)

zaś względny błąd pomiaru γ (w procentach) jest obliczany z zależności (3):

. (3)

Podczas pomiarów takim przyrządem, oprócz zanotowania odczytanej wartości mierzonej wielkości i klasy przyrządu obowiązkowo należy zanotować zakres pomiarowy X_zakr, przyrządu. Zaniechanie tego uniemożliwi obliczenie względnego błędu pomiaru. Warto podkreślić, że względny błąd pomiaru γ jest równy klasie przyrządu jedynie dla X=X_zakr. Przy X = 0,1X_zakr względny błąd pomiaru γ jest 10 razy większy niż γ_a, a przy dalszym zmniejszaniu X błąd pomiaru dąży do nieskończoności (rys.1c). Przy zmniejszaniu wielkości mierzonej X do wartości X_min=Δ_a, względny błąd pomiaru osiąga 100%, tzn.:

. (4)

Taka wartość wielkości mierzonej X, dla której względny błąd pomiaru γ wynosi 100%, nazywa się progiem czułości przyrządu. Ponieważ dla małych X względny błąd pomiaru γ przyjmuje bardzo duże wartości to zakres użytkowy przyrządu - zwany zakresem dynamicznym D (rys.1c) - jest ograniczany od dołu do takiej wartości, dla której γ wynosi np. 4%, 10%. Na początku skali pomiary są niedopuszczalne, co wynika z ujemnego wpływu błędu addytywnego nie pozwalającego wykorzystać tego samego przyrządu do pomiarów zarówno małych jak i dużych wartości wielkości mierzonej bez zmiany zakresu.

Źródłem błędów addytywnych są szumy, dryfty, tarcie w łożyskach, wibracje, pola postronne, indukowane napięcia, nieuniknione siły termoelektryczne itp. W celu minimalizacji błędu addytywnego przyrządy pomiarowe wyposażane są w tzw. korektory zera - mechaniczne lub elektryczne.

3. Szacowanie błędów przy normalizacji multiplikatywnej

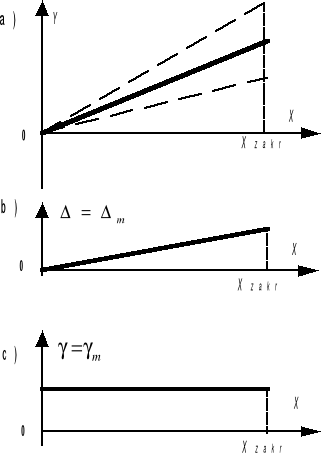
Przy normalizacji multiplikatywnej punkty kalibracyjne (a więc i charakterystyka statyczna narzędzia pomiarowego) układają się w obszarze rozszerzającym się proporcjonalnie do wzrostu wielkości mierzonej X, a przy X=0 szerokość obszaru także jest równa zero (rys.2a). Taki błąd nazywa się błędem multiplikatywnym lub błędem czułości, niezależnie od tego czy źródło tego błędu jest o charakterze przypadkowym czy systematycznym. Przyczynami błędów multiplikatywnych mogą być: zmiana stałej sprężynek wytwarzających moment zwracający w przyrządach elektromechanicznych, zmiana współczynnika wzmocnienia wzmacniacza pomiarowego, zmiana wartości napięcia wzorcowego w przetwornika A/C przyrządów cyfrowych itp.

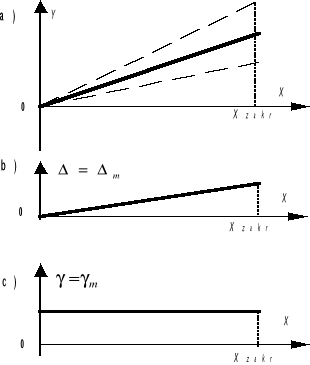
Rys. 2. Ilustracja normalizacji multiplikatywnej

Błąd bezwzględny multiplikatywny Δ_m wzrasta proporcjonalnie wraz ze wzrostem wielkości mierzonej X (rys.2b), a więc względny błąd multiplikatywny γ_m, t.j. błąd czułości takiego narzędzia pomiarowego:

(5)

jest stały przy dowolnej wartości X (rys.2b).Właśnie, wyrażony w procentach, γ_m jest wykorzystywany do normalizacji błędów i oznaczenia klasy dokładności tego typu narzędzi pomiarowych. W celu podkreślenia różnicy w stosunku do normalizacji addytywnej, klasa przyrządów o normalizacji multiplikatywnej jest podawana w postaci liczb umieszczonych
w okręgu np.:

W tym przypadku, wyrażony w procentach, względny błąd pomiaru γ (6) jest równy klasie przyrządu:

, (6)

zaś bezwzględny błąd pomiaru Δ (7), w jednostkach wielkości mierzonej, jest obliczany
z zależności:

. (7)

Jeśliby zależności (6) i (7) obowiązywały w całym zakresie pomiarowym, od X=0 do X=X_zakr to tego typu narzędzia pomiarowe byłyby najbardziej doskonałymi, ponieważ posiadałyby nieskończenie wielki zakres dynamiczny. Oznaczałoby to, że umożliwiałyby pomiar, z tym samym błędem, dowolnie małych wielkości. W związku z nieuchronną obecnością szczątkowych błędów addytywnych dla realnych narzędzi pomiarowych
z multiplikatywną normalizacją dokładności, zawsze podawane są granice zakresu pomiarowego (pewne X_min), w którym taka ocena błędów pomiarów jest w przybliżeniu możliwa.

Normalizacja multiplikatywna ma zastosowanie w odniesieniu do przetworników skali, a więc dzielników napięcia, boczników, przekładników napięciowych i prądowych,
a także liczników energii elektrycznej i liczników ilości ciepła, dla których nie można uwzględnić zmian X (zmian mocy elektrycznej lub cieplnej), ponieważ dostępna jest jedynie całka z tej wielkości. Warto zaznaczyć, że w przypadku liczników energii trudno byłoby mówić o zakresie pomiarowym.

4. Szacowanie błędów przy normalizacji addytywno-multiplikatywnej

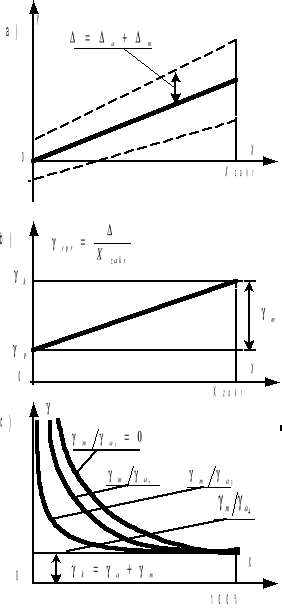
Gdy błędy, addytywny i multiplikatywny, przyrządu pomiarowego mają współmierne wartości jego strefa błędów posiada kształt trapezu (rys. 3a), którego ramiona ograniczają położenie charakterystyki przetwarzania. Błąd bezwzględny Δ jest równy sumie błędów addytywnego Δ_a i multiplikatywnego Δ_m, a więc po uwzględnieniu (5) możemy napisać:

. (7)

Jeżeli strony (7) podzielić przez wartość zakresową X_zakr otrzymuje się tzw. błąd sprowadzony γ_spr, przedstawiony na rys.3b):

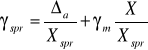
. (8)

Tak więc w obecności zarówno składowej addytywnej jak i multiplikatywnej, błąd sprowadzony przyrządu pomiarowego rośnie liniowo (rys.3b) od
dla X=0, a więc na początku zakresu, do
do X=X_zakr, a więc na końcu zakresu.

Po uwzględnieniu (1) oraz (7) względny błąd pomiaru γ, przyrządem o normalizacji addytywno-multiplikatywnej, wyrazi się zależnością (9):

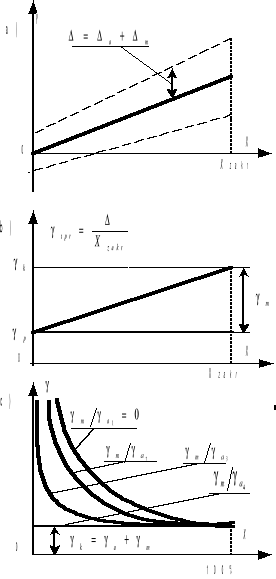
. (9)

Rys.3 Ilustracja normalizacji addytywno-multiplikatywnej dla γ_a4 < γ_a3 < γ_a2 < γ_a1

Dla X=X_zakr, względny błąd pomiaru

, i w miarę zmniejszania X rośnie do nieskończoności jak to pokazano na rys.3c). Jednakże w tym przypadku zmiana γ, w porównaniu z błędem przy czysto addytywnym charakterze, jest zauważalna tym później im mniejszy jest γ_a w porównaniu z γ_m. Z przebiegu krzywych z rys.3c) zauważamy, że zakres roboczy przyrządu ulega rozszerzeniu w miarę wzrostu γ_m/γ_a, tj. przy zmniejszaniu Δ_a i przybliżaniu charakteru błędów do błędów czysto multiplikatywnych rozważanych w p. 2.

Przedstawiony na rys.3 charakter błędów jest właściwy dla cyfrowych multimetrów a także dla kompensatorów napięcia stałego i innych precyzyjnych przyrządów. Charakterystycznym jest to, że w dokumentacji tego typu przyrządów nie jest podawana klasa dokładności lecz wzory służące do obliczania błędów pomiarów. Postać tych wzorów nie jest jednolita i zależy od kraju pochodzenia wytwórcy przyrządu.

W dokumentacji wytwórców przyrządów z krajów anglosaskich, dokładność najczęściej jest charakteryzowana przez podanie, wyrażonych w procentach, względnego błędu multiplikatywnego γ_m i względnego błędu addytywnego γ_a (± γ_m% of reading ± γ_a% of range). W tym przypadku, uwzględniając (7), bezwzględny błąd pomiaru Δ, w jednostkach wielkości mierzonej, obliczamy z wzoru (10):

, (10)

zaś względny błąd procentowy bezpośrednio z wzoru (9).

Niekiedy błąd bezwzględny addytywny
Δ_a podawany jest jako liczba najmniej znaczących cyfr niepewnych z (± γ_m% of reading ± z digit). Wówczas błąd bezwzględny pomiaru Δ, w jednostkach wielkości mierzonej, należy wyliczyć z wzoru (11):

, (11)

zaś względny błąd procentowy γ z zależności (12):

. (12)

W dokumentacjach technicznych przyrządów wyprodukowanych w byłych krajach socjalistycznych, dla przyrządów o normalizacji addytywno-multiplikatywnej, podaje się ich klasę dokładności, jednak w postaci dwucyfrowej γ_k/γ_p (np.0,02/0,01). Uzasadnienie dla takiego sposobu oznaczenia klasy przyrządu otrzymujemy przekształcając wzór (9) do postaci:

, (13)

z której, po przekształceniach i przyjęciu oznaczeń z rys.3b) i rys.3c), otrzymujemy wzór (14) do obliczenia względnego procentowego błędu pomiaru:

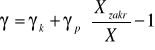
(14)

i wzór (15) umożliwiający obliczenie bezwzględnego błędu pomiaru, w jednostkach wielkości mierzonej

(15)

4. Podsumowanie

Szereg narzędzi pomiarowych charakteryzuje się bardziej złożoną strefą błędów niż te strefy, które zostały przedstawione na rys.1, rys.2 i rys.3. Na przykład:

• błędy cyfrowych częstościomierzy zależą nie tylko od wartości wielkości mierzonej, lecz także od czasu pomiaru,

• mostki do pomiarów rezystancji charakteryzują się tym, że posiadają dolny i górny próg czułości, dla których błędy osiągają 100%,

• błędy najdokładniejszych kompensatorów napięcia stałego normalizowane są zgodnie
  z zależnością (7), a ich klasa dokładności podawana jest za pomocą jednej liczby γ_m itd.

We wszystkich tego typu sytuacjach należy dokładnie analizować dokumentację przyrządu i wykorzystywać, dla obliczenia błędów pomiarów, zawarte w niej specjalne formuły.

1

J.R. Jasik 5.02.2011

---