• Laboratorium fizyki CMF PŁ

• Dzień 04.10.2007 godzina 10¹⁵ grupa 6

Wydział Elektrotechnika

semestr I rok akademicki 2007/08

ocena _____

Wstęp teoretyczny:

Efekt Halla możemy występuje w przewodnikach i półprzewodnikach gdzie prędkość dryfu nośników prądu V_p jest różna od zera.

Jeżeli przez płytkę półprzewodnika (przewodnika) popłynie prąd o natężeniu I, i jednocześnie poddamy działaniu zewnętrznemu polu magnetycznemu o wartości indukcji B, skierowanym prostopadle do naszej płytki, na nośniki prądu zacznie działać siła zakrzywiająca ich tory ruchu, siła Lorenza - F_L której kierunek zależy od rodzaju nośnika prądu (dodatniego, bądź ujemnego). Wytworzy się wówczas pole elektryczne E_H, zwanym polem Halla, którego siła F
równoważyć będzie działanie siły F_L, w wyniku czego w ptk. A i Z wytworzy się różnica potencjałów i powstanie napniecie Halla - U_H. wyrażające się wzorem:

Gdzie:

R - to współczynnik proporcjonalności (stała Halla)

B - indukcja magnetyczna pola

j - gęstość prądu

d - szerokość płytki

Opis sprzętu użytego w doświadczeniu:

Do pomiarów wartości natężenia prądu, napięcia Halla i wartości indukcji elektromagnetycznej użyte zostały:

1. Miliwoltomierz, badający napięcie poprzeczne U_H, podłączony do ptk A i B naszej płytki.

2. Miliamperomierz mierzący natężenie prądu I w badanej próbce.

3. Teslometr badający wartość pola magnetycznego połączony z czujnikiem pola - Hallotronem.

4. Elektromagnes wytwarzający poprzeczne względem próbki pole magnetyczne.

5. Statyw utrzymujący próbkę.

6. Przewody łączące poszczególne części zestawu.

7. Zasilacz.

Opis pomiaru:

Badaliśmy zachowanie U_H w zależności od wartości indukcji pola B oraz natężenia prądu I płynącego w próbce o wymiarach

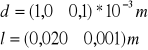
I oporności R₀

Dla ustawionej jednej stałej wartości, natężenia lub indukcji, przeprowadzone zostały pomiary, których wyniki widnieją w tabelach poniżej.

1. badanie napięcia U_H Halla w funkcji natężenia I

U_H = f(I)

B [mT]	100
I [mA]	5	10	15	20	25	30	35	40
UH [mv]	1	5	11,5	17,1	23,8	31,2	36,2	42

a = 1.211 - współczynnik kierunkowy prostej
a = 0.027 korelacja = 0,998

b = -6.282 - wyraz wolny
b = 0.670

B [mT]	150
I [mA]	5	10	15	20	25	30	35	40
UH [mv]	2,4	11,1	19,2	27,8	37,5	43,9	54,5	62,6

a = 1.729 - współczynnik kierunkowy prostej
a = 0.0225 korelacja = 0,999

b = -6.314 - wyraz wolny
b = 0.569

B [mT]	200
I [mA]	5	10	15	20	25	30	35	40
UH [mv]	6,2	17,1	29,5	41,4	54,9	65,4	78,1	89

a = 2.395 - współczynnik kierunkowy prostej
a = 0.021 korelacja = 0,999

b = -6.182 - wyraz wolny
b = 0.541

2. badanie napięcia U_H Halla w funkcji wartości indukcji B

U_H = f(B)

I [mA]	10
B [mT]	50	100	150	200	250
UH [mv]	1,6	5,3	11,7	17,8	24,2

a = 1.154 x 10^-1- współczynnik kierunkowy prostej
a = 0.059 x 10^-1 korelacja = 0,996

b = -5.19 - wyraz wolny
b = 0.979

I [mA]	20
B [mT]	50	100	150	200	250
UH [mv]	3,2	16,2	28,3	40,5	51,6

a = 0.621 x 10^-1 - współczynnik kierunkowy prostej
a = 0.023 korelacja = 0,999

b = -6.314 - wyraz wolny
b = 0.569

I [mA]	30
B [mT]	50	100	150	200	250
UH [mv]	7,5	26,7	45,1	61,3	78

a = 3.512 x 10^-1- współczynnik kierunkowy prostej
a = 0.074 x 10^-1 korelacja = 0,999

b = -8.96 - wyraz wolny
b = 1.227

Wyznaczenie stałej Halla :

Do wyznaczenia stałej Halla R_H należy wziąć wykres zależności napięcia Halla w funkcji natężenia prądu U_H = f(I)

Wykres zmian napięcia względem natężenia ma charakter liniowy y = ax + b, gdzie a stanowi współczynnik kierunkowy prostej.

ponieważ
a
gdzie S oznacza pole przekroju poprzecznego przewodnika

zatem wartość stałej Halla wynosi po obliczeniach:

Dla B =100 [mT].

R_H = 0,121

Dla B =150 [mT]

R_H = 0,173

Dla B =200 [mT]

R_H = 0,239

Wnioski:

Znak przy stałej Halla jest dodatni, z czego wynika, ze w badanej próbce nośnikami prądu są ładunki dodatnie tzw. „dziury” jest to zatem półprzewodnik typu „p”.

Wielkość natężenia prądu płynącego próbce nie ma wpływu na wartość stałej Halla.

Wyznaczenie koncentracji nośników prądu:

Przyjmując, że e = 1.61 x 10^-19 C a koncentrację nośników nazwiemy p możemy napisać, że:

Dla R_H = 0,121

Dla R_H = 0,173

R_H = 0,239

Wnioski:

Koncentracja nośników prądu maleje wraz ze wzrostem wartości pola magnetycznego.

Wyznaczanie ruchliwości:

Znając wartości współczynnika Halla R_H, koncentracji nośników (n lub p) i oporność próbki R_o oraz jej długość l, określamy wielkość zwaną ruchliwością nośników prądu

Dla R_H = 0,121

Dla R_H = 0,173

Dla R_H = 0,239

Wnioski:

Ruchliwość nośników prądu wzrasta wraz z wzrostem wartości pola magnetycznego.

Podsumowanie:

Metoda ta wyznaczania stałej Halla, ruchliwości nośników oraz ich koncentracji przy użyciu dokładnych urządzeń pomiarowy jest skuteczna.

Za pomocą tego doświadczenia można określić rodzaj badanej próbki, a na podstawie znaku przy stałej Halla rodzaj nośników prądu.

Stopień popełnienia błędu sądząc po korelacji linii prostej na wykresach jest nieznaczny.

Przyczyny powstawania błędów:

• niedokładności urządzeń pomiarowych..

• niedokładności ludzkiej ręki ustawiającej parametry

• stopniowe nagrzewanie się próbki, co zmniejsza oporność i wpływa na wyniki

Literatura:

I.W. Sawielew Kurs Fizyki, Warszawa 1989r.

Kod ćwiczenia	Tytuł ćwiczenia
E1a	Efekt Halla w germanie typu „p”

Przemysław Radecki

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu _ _ _ _ _ _145268_ _ _ _

Przemysław Kostrzewa

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu _ _ _ _ _ _ _ _ _ _ _ _

Adrian Fronk

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

imię i nazwisko

nr indeksu _ _ _ _ _ _ _ _ _ _ _ _

---