1.Iloczyn skalarny i wektorowy

a)Ilocz. Skalarny a*b=|a|*|b|*cos<(a,b)[rzut wektora b na kierunek a]
Własności: - Przemienny: a*b = b*a

- Jeśli a ↓ b => a*b=0 e_x*e_x=1; e_y*e_y=1;

- e_z*e_z=1 e_x*e_y=0; e_x*e_z=0; e_y*e_z=0

- a*b= a_xb_x+a_yb_y+a_zb_z

b)Iloczyn Wektorowy axb = c; c ↓ a; c ↓ b
Własności: -Nie przemienny axb = -bxa

-Jeśli a || b => axb=0

2.Punkt materialny. Układ odniesienia. Względność ruchu.

a)Punkt materialny (masa punktowa) - ciało fizyczne obdarzone masą, ale mające nieskończenie małe rozmiary (będące punktem).

b) Punkt materialny nie jest obiektem istniejącym w rzeczywistości. Jego stosowanie jest przybliżeniem i upraszcza znacząco opis ruchu danego ciała.

3.Wektor wodzący. Prędkość liniowa. Przyspieszenie liniowe. Przyspieszenie styczne i normalne.

a)Wektor Wodzący - wektor opisujący położenie punktu materialnego r = r(t) r = [x,y,z] r = x_ex +y_ey + z_ez

b)Prędkość Liniowa - wektor prędkości jest styczny do toru

V_x = dx/dt = x' V_y = dy/dt = y' V_z = dz/dt = z'

c)Przyspieszenie Liniowe - zmiana prędkości w czasie

a_x = dV_x/dt = V_x' = x'' a_y = dV_y/dt = V_y' = y'' a_z = dV_z/dt = V_z' = z''

d)Przyspieszenie Styczne i Normalne

- a^2 = a_s ²+ a_n²

- a_s = d|V|/dt związane ze zmianą wartości prędkości

- a_n = V ² /r związane ze zmianą kierunku prędkości

4.Zasady dynamiki Newtona dla ruchu postępowego.

a) I Zasada Dynamiki Newtona - Zasada Bezwładności - Jeżeli na punkt materialny nie działają żadne siły lub działające siły się równoważą to ciało pozostaje w spoczynku albo porusza się ruchem jednostajnym

b) II Zasada Dynamiki Newtona - Przyśpieszenie punktu materialnego ma wartość proporcjonalną do wartości siły działającej na ten punkt i ma kierunek siły F = m*a; F = p' (p - pęd)

c) III Zasada Dynamiki Newtona - Akcją i Reakcja - Siły, które wywierają na siebie dwa punkty materialne są równe, co do wartości, są skierowane wzdłuż prostej łączącej te punkty oraz zwrócone przeciwnie F_AB = -F_BA

5/Siła zachowawcza. Związek między siłą a energią potencjalną. SIŁA TARCIA

a)Siła Zachowawcza - Siła Potencjalna - ∫Fds = 0 (np. siła grawitacji)

- Siła Tarcia nie jest siła zachowawczą

- Praca siły zachowawczej nie zależy od kształtu drogi, ale od punktu początkowego i końcowego

b) Związek siły i energii potencjalnej:
E_pot = mgh ; ∫Fds = 0

6.Praca siły stałej i zmiennej w czasie.

a)Praca siły Stałej w czasie: W = F*s = F*s*cos<(F,s)
b)Praca siły Zmiennej : F₁*ds₁ + F₂*ds₂+ … F_n*ds_n W = ∫Fds

c) Tarcie to całość zjawisk fizycznych towarzyszących przemieszczaniu się względem siebie dwóch ciał fizycznych (tarcie zewnętrzne) lub elementów tego samego ciała (tarcie wewnętrzne) i powodujących rozpraszanie energii podczas ruchu.

, współczynnik tarcia*siła nacisku

7.Układy inercjalne i nieinercjalne, siły bezwł, dośrd, odśrd

a)Układ inercjalny to taki układ odniesienia, który porusza się ze stałą prędkością po linii prostej. Innymi słowy, jego wektor prędkości nie zmienia się. Stałe pozostają jego kierunek, zwrot i wartość.
b) Układ nieinercjalny to układ odniesienia, którego wektor prędkości zmienia się, czyli taki, który ma niezerowe przyspieszenie.
c) Siła bezwładności (siła inercji, siła pozorna) - siła pojawiająca się w nieinercjalnym układzie odniesienia, będąca wynikiem przyspieszenia tego układu. F=-m*a

d) Siła dośrodkowa - siła powodująca zakrzywianie toru ruchu ciała, skierowana wzdłuż normalnej (prostopadle) do toru, w stronę środka jego krzywizny. F=(mv^2)/r r-promień krzywizny toru

e) Siła odśrodkowa  - jedna z sił bezwładności występująca w obracających się układach odniesienia. Układy takie zalicza się do układów nieinercjalnych. F=(mv^2)/r r-promień krzywizny toru

8.Ruch obrotowy. Prędkość kątowa i przyspieszenie kątowe. Przyspieszenie dośrodkowe.

a)Droga Kątowa φ

b)Prędkość kątowa ω = dφ/dt lub ω=V/R

c)Przyspieszenie kątowe α = dω/dt

d) Przyspieszenie dośrodkowe - wektor prostopadły do osi obrotu, przedstawiający odległość punktu bryły od osi obrotu

e)Okres ruchu T=t/N, N-ilość wykonanych okrązen, t - czas

f)Częstotliwość  f=N/t

9.Pęd. Moment pędu. Moment siły.

a)Pęd - p = m*V F = dp/dt Pęd - w mechanice wielkość fizyczna opisująca ruch obiektu fizycznego.

b)Moment Pędu (Kręt) - K = r x p = r x (m*v) i r ↓ V => K = rmv = mωr²

c)Moment Siły - M = r x F, r - promień wodzący |M|=|s|*|F|sin<(s;F)

10.Układ środka masy (współrzędne środka masy, twierdzenie o ruchu środka masy).

a)Środek masy może być określony jako punkt mający tę właściwość, że wektor wodzący tego punktu pomnożony przez masę układu równa się sumie iloczynów wektorowych wodzących wszystkich punktów układów pomnożonych przez ich masy.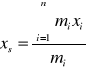

b)F_zew = mr_s = ma_s

11.Moment bezwładności bryły sztywnej. Twierdzenie Steinera.

a)Moment bezwładności: I = Σm_i*r_i²

b)Twierdzenie Steinera: I = I₀ + md² Moment bezwładności względem dowolnej osi jest równy sumie momentu bezwładności względem osi przechodzącej przez środek masy (oś równoległa) i iloczyny masy bryły o kwadratu odległości względem obu osi

12/Energia kinetyczna ruchu obrotowego bryły sztywnej. Moment pędu bryły sztywnej. Energia kinetyczna postępowa

a)Energia kinetyczna ruchu obrotowego: E_k = ½ Iω²

b)Moment pędu bryły sztywnej: K = Iω

c) E_k=mV²/2

13.Zasady zachowania w mechanice

a)Zasada Zachowania Energii Mechanicznej

- Układy odosobnione - nie działają żadne siły zewnętrzne

- Układy zachowawcze - siły wewnętrzne siłami zachowawczymi, praca po torze zamkniętym=0

- Energia mechaniczna układu odosobnionego i zachowawczego jest stała E_kin + E_pot = const

b)Zasada Zachowania Pędu - pochodna całkowitego pędu układu równa się wypadkowej sile zewnętrznej działającej na układ

Suma wektorowa pędów wszystkich elementów układu izolowanego pozostaje stała.
F_i = dp_i/dt_i Σ F_i = d/dt * Σ p_i F_zew = 0 => p=const

c)Zasada Zachowania Momentu Pędu

- Mz = dK/dt Mz= 0 => K=const

14.Zderzenia sprężyste i niesprężyste.

a)Zderzenia Sprężyste - Występuje Zasada Zachowania Pędu i Energii (m₁V₁²)/2 + (m₂V₂²)/2 = (m_1kV_1k²)/2 + (m_2kV_2k²)/2

b)Zderzenie Niesprężyste - Wstępuje Zasada Zachowania Pędu
m₁V₁² + m₂V₂² = (m₁ + m₂)V _końcowe

15.Zasady dynamiki Newtona dla ruchu obrotowego.

a)II Zasada M=I*α (M = dK/dt; M = I*dω/dt = I*α)

b)III Zasada M_AB = -M_BA

b)I Zasada M=0 =>α=0 bryla pozostaje w spoczynku lub porusza się ruchem jednostajnie obrotowym

16.Pole grawitacyjne (Prawo grawitacji Newtona. Energia w polu grawitacyjnym. Prędkości kosmiczne), prawa Keplera

a)Prawo Grawitacji Newtona: F_gr = G(Mm/r²) G=6,672*10^-11

b)Energia w polu grawitacyjnym (praca siły zachowawczej): Ep(r) = W_p(r) = -GMm/r <0 E_p (∞) = 0

c)Prędkości Kosmiczne:

- I Prędkość: Minimalna prędkość jaką należy nadać ciału aby poruszało się po stabilnej orbicie (wokół Ziemi) V_I = √GM/R

- II Prędkość (prędkość ucieczki): Minimalna prędkość umożliwiająca osiągnięcie nieskończonej odległości od planety V_II = √2GM/R

d)I prawo keplera: Każda planeta Układu Słonecznego porusza się wokół Słońca po elipsie, w której w jednym z ognisk jest Słońce

e)II prawo keplera:w równych odstępach czasu, promień wodzący planety poprowadzony od Słońca zakreśla równe pola.

f)III prawo keplera: Stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu wielkiej półosi jej orbity (czyli średniej odległości od Słońca) jest stały dla wszystkich planet w Układzie Słonecznym

17.Postulaty szczególnej teorii względności.

a)Zasadzie względności: Zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych — musi obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki.

b)Niezmienność prędkości światła: Prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła światła.

18.Transformacja Galileusza i transformacja Lorentza.

a)Tr. Galileusza: zależności między współrzędnymi przestrzenno-czasowymi dowolnego zdarzenia rozpatrywanego w 2 różnych inercjalnych układach odniesienia poruszających się względem siebie prostoliniowo i jednostajnie z prędkością. Dla V << c
r = r + V*t V = V' + V

b)Tr. Lorentza: dla V zbliżonego do c. Jeśli V<<c Tr. Lorentza przechodzi w Tr. Galileusza γ = 1/√[1-(v²/c²)]

19.Relatywistyczne składanie prędkości.

(v_x, v_y, v_z — składowe prędkości ruchu układu K' względem układu K)
v: x = x' + v_xt', y = y' + v_yt', z = z'  + v_zt', t = t'

20.Skrócenie Lorentza: Ciało poruszające się z dużą prędkością ulega skróceniu w kierunku ruchu
l = l₀/γ = l₀√[1-(v²/c²)]

21.Zagadnienie jednoczesności w STW: Jednoczesność zdarzeń zależy od układu odniesienia, a czas nie ma charakteru absolutnego.

22.Dylatacja czasu w STW: w teorii względności efekt polegający bądź na opóźnianiu się zegara będącego w ruchu w stosunku do zegara spoczywającego w pewnym inercjalnym układzie odniesienia (kinematyczna dylatacja czasu), bądź na opóźnianiu się zegara znajdującego się w silnym polu grawitacyjnym (grawitacyjna dylatacja czasu) t=γt'

23.Relatywistyczny efekt Dopplera. Przesunięcie ku czerwieni.

a)Zjawisko Dopplera uwidacznia się przesunięciem linii w widmie optycznym w kierunku fioletu lub czerwieni, w zależności od tego, czy następuje zbliżenie, czy oddalenie odbiornika i źródła światła; jest też przyczyną poszerzania linii widmowych światła emitowanego przez atomy gazu wykonujące chaotyczne ruchy termiczne (poszerzenie dopplerowskie); wykorzystywane m.in. w astrofizyce do badania gwiazd podwójnych, w miernikach radiolokacyjnych (dopplerowskich)

b)Przesunięcie Ku Czerwieni: przesunięcie widma promieniowania ciała niebieskiego w kierunku fal długich, wynikające ze zmiany długości fali tego promieniowania mierzonej na Ziemi w porównaniu z długością fali emitowanej przez ciało; wynik zjawiska Dopplera lub poczerwienienia grawitacyjnego.
ω = 2Π/T = 2Πc/λ ω = ω₀√[1-(v/c)]/ [1+(v/c)] ω - odbieranie ω₀ - wysłanie

24.Przestrzeń Minkowskiego:
a)Przestrzeń Minkowskiego - czterowymiarowa przestrzeń stosowana do opisu zjawisk fizycznych w szczególnej teorii względności; trzy wymiary tej przestrzeni odpowiadają trzem wymiarom przestrzennym, a czwarty - czasowi

b)Zdarzenie można umiejscowić w czasoprzestrzeni przez podanie jego 4 współrzędnych: trzech określających położenie i czwartej - czasu

c)Interwał: odległość miedzy dwoma zdarzeniami. Niezmienność Interwałów: ds² = dx² + dy² + dz² - c²dt² = (x₂-x₁ )² +(y₂-y₁)² +(z₂-z₁)² -(ct₂-ct₂)² ds² = dx² - c²dt²
ds'² = dx'² - c²dt'² dx'= γ(dx-(v²/c²)dx)
ds²=ds'²
d)Rodzaje Interwałów:

- Interwał przestrzenny - nie można powiązać przyczynowo ds^2>0

- Interwał zerowy - można powiazć sygnałem o prędkości V=c ds^2=0

- Interwał czasowy - można powiązać przyczynowo ds^2<0

25.Stożek świetlny
a)Podział Czasoprzestrzeni - 4 współrzędne określające zdarzenie: 3 współrzędne przestrzenne i czas

b)Odwrócenie kolejności zdarzeń gdy nie są dwa zdarzenia powiązane przyczynowo.

26.Równoważność masy i energii - wzór Einsteina. Masa relatywistyczna, pęd relatywistyczny

a)Równoważność masy: m = γm₀ m - masa relatywistyczna m₀ - masa spoczynkowa

b)Energia: E = mc² E₀ = m₀c² Ek = E - E₀

c) E²=p²c²+m²c⁴
27.Defekt masy i energia wiązania
a)Defekt masy - różnica między sumą mas poszczególnych składników układu fizycznego a masą tego układu; dla jądra atom. złożonego z Z protonów i N neutronów niedobór masy wynosi Δ(Z, N) = Zm_p + Nm_n - m (Z, N), gdzie m_p - masa protonu, m_n - masa neutronu, m(N, Z) - masa jądra; niedobór masy jest miarą energii wiązania układu.
b)energia wiązania - energia, jaką trzeba dostarczyć układowi fizycznemu (np. cząsteczce, jądru atom.), aby rozdzielić go na poszczególne składniki. Ubytekmasy E maleje przyrost masy E rosnie E=mc^2
28.Foton, jego energia i masa, pęd
a)Foton - cząstka elementarna niemająca ładunku elektrycznego, o masie spoczynkowej m₀ = 0, spinie 1 ħ; jest nośnikiem oddziaływań elektromagnetycznych; stanowi kwant energii promieniowania elektromagnetycznego
b)Energia fotonu E = h (h — stała Plancka,  — częstość promieniowania), pęd p = h/c
c)Masa spoczynkowa m₀ = 0\

d) Pęd fotonu p jest określony wzorem p=h/ λ=hf/c. Foton (jako cząstka) oddziałując z materią podczas odbicia, pochłonięcia czy emisji zmienia swój pęd, a tym samym i pęd ciała, z którym oddziałuje.

29. OTW. Efekty fizyczne przewidywane przez OTW
Zasada równoważności: prawa fizyki są takie same we wszystkich układach odniesienia (trzeba je tylko odpowiednio zapisać)

a)Odchylenie toru światła α=4GM/Rc²

b)Precesja geodezyjna- Obrót osi orbity planet wokół słońca deltaφ=6piGM/rc² M - masa słońca, r - promień orbity

C)Grawitacyjne opóźnienie Zegarów: dτ = √(1-2GM/Rc²)dt
D)Grawitacyjny efekt Dopplera -grawitacyjne przesunięcie prążków widmowych ku czerwieni
30. Czarne dziury
a)Czarne dziury - obiekt będący źródłem na tyle silnego pola

grawitacyjnego, że niemożliwe jest przesłanie zeń na zewnątrz żadnej informacji
b)Promień Schwarzschilda (promień grawitacyjny) - Jeśli promień grawitacyjny jest większy od promienia geometryczny, to prędkość ucieczki z powierzchni ciała przekracza prędkość światła, a zatem z ciała tego nie może wydostać się żaden rodzaj materii; ciało takie nazywa się czarną dziurą r_g = 2Gm/c²
c)Osobliwość i Horyzont zdarzeń
31.Efekty fizyczne w pobliżu czarnej dziury
a)Siły pływowe - „rozlewanie” się ciał
b)Rotacja (wleczenie)
32.Odległości w astronomii (rok świetlny)
a)Rok świetlny - jednostka długości w stosowana w astronomii. Odległość, którą światło przebiega w próżni w ciągu roku; 1 rok świetlny = 9,46 ∙ 10 ¹² km = 0,307 pc
33.Proste drgania harmoniczne (amplituda, okres, pulsacja, faza początkowa, energia punktu drgającego). Równanie różniczkowe drgań swobodnych. Składanie drgań równoległych - dudnienia
a)Proste drgania harmoniczne - składowe drgań o częstości równej wielokrotności częstości podstawowej. x = Acos(ωt+φ)
b)Amplituda - największa wartość A₀ osiągana przez wielkość fizyczną A zmieniającą się w czasie t w sposób harmoniczny
c)Okres - Czas potrzebny do wykonania jednego cyklu drgań. T = 1/f [Hz] T = 2Π√m/√k
d)Pulsacja - Częstość własna: ω² = √k/m. Okresowa zmiana jakiejś wielkości fizycznej. Faza początkowa - φ
e)Energia punktu drgającego - E_c = E_k + E_p E = mv²/2 + kx²/2 E=A²k/2
f)Równanie Różniczkowe drgań swobodnych: ξ = ξ(x,t)

F_s=-kx II zasada: ma=F_s=>
+(k/m)x=0
x=A₀cos(ω₀+φ) E_c=E_k+E_p=1/2mv²+1/2kx²=1/2kA₀² A₀-> amplituda E=const Spełnione zostają zasady zachowania energii mechan.

Prędkość Falowa - V= ω/k
g)Składowe drgań równoległych - Dudnienie
x₁ = A*cosωt x₂ = A*cos[(ω+Δω)t
x = x₁+ x₁ = A*cosωt + A*cos[(ω+Δω)] = 2A*cos[(ω+Δω/2)t]cos(Δωt/2) = 2A*cos(Δωt/2)cos(ωt)
34.Drgania tłumione. Logarytmiczny dekrement tłumienia.
a)Drgania Tłumione: β - Współczynnik tłumienia
F_t=-bv b-współczynnik oporu (dla małych v) II zasada: Ma=F_s+F_t => ma+bv+kx=0 e+(b/m)v+(k/m)x=0 {
+2B(dx/dt)+ ω₀²x=0; d²x+2B(dx/dt)+ ω₀²x=0} Rozw: x=A₀^-Btcos(ω₀t+ φ) Pulsacja drgań tłumionych ω₁=
ω - częstość drgań układu bez tłumienia B=b/2m
b)Logaryt Dekrement Tłumienia - Λ=ln[A(t)/A(t+T)] = β*T
c)Tłumienie krytyczne - stan przejściowy pomiędzy tłumieniem wykładniczym a ruchem periodycznym a = ω
d)Tłumienie nadkrytyczne - układ powoli przechodzi do położenia równowagi i nie wykonuje dalszych drgań β> ω₀
35.Drgania wymuszone.
a)Drgania wymuszone - układ na który działa okresowo zmienna siła zewnętrza. siła wymuszająca F_w=F_ocos(Ωt+φ) Ω-pulsacja siły F_w, F_o-amplituda F_w II zasada: ma=F_W+F_T+F_S =>
+2B
+ ω₀²x+(F₀/m)cos(Ω+φ) ROZW: x=Ae^-Btcos(ωt+φ)+Acos(Ω+ϕ)

b)Rezonans - szybki wzrost amplitudy drgań układu fizycznego, gdy częstość zewnętrzna drgań wymuszających f jest zbliżona do częstości drgań własnych układu f₀ . dA/dΩ=0 => Ω_R=
- pulsacja rezonansu A_n=(F₀/m)/2B
- amplituda rezonansu
36.Fala poprzeczna i podłużna
a)Fala poprzeczna - kierunek drgań cząsteczek ośrodka prostopadła ( ↓ )do kierunku rozchodzenia się
b)Fala podłużna - Kierunek drgań równoległy ( | | ) do kierunku rozchodzenia się
c)Fala płaska - powierzchnie falowe są płaszczyznami; promienie fali prostymi | | rozchodzi się w jednym kierunku
d)Fala kulista - powierzchnie falowe sferami; promienie fali promieniami sfery, rozchodzi się w różnych kierunkach
e)Fala monochromatyczna - nieograniczona w przestrzeni fala o okreslonej dlugosci i czestotliwosci
Długość Fali - λ = V*T = V/f Wektor falowy - k=2Π/λ
ξ = A*sin(k*r - ω*t) ω = 2Π/T ξ = A*sin[(2Π/λ)(x - v*t)]
37.Interferencja i dyfrakcja fal. Fale stojące. Zasada Huygensa
a)Interferencja Fal (superpozycja)- nakładanie się 2 lub więcej fal prowadzące do zwiększenia lub zmniejszenia amplitudy fali wypadkowej w zależności od różnicy faz fal składowych
ξ = ξ₁ + ξ₂ = [A*sin(k*x - ω*t) + A*sin(k*x - ω*t + φ)] = 2A*cos(φ/2)sin(k*x - ω*t + φ/2)
b)Dyfrakcja Fal - Zniekształcenie powierzchni fali
c)Fale Stojące - w falach tych wyróżnia się punkty, w których zaburzenie stale znika - węzły i punkty, w których zaburzenie ma w określonej chwili wartość maksymalnej - strzałka
d)Zasada Huygensa - każdy punkt ośrodka, do którego dochodzi czoło fali, staje się źródłem fal elementarnych; obwiednia tych fal tworzy nową powierzchnię falową.
38.Ładunek elementarny. Ziarnistość ładunku
a) Ładunek elementarny - najmniejszy ładunek elektryczny występujący samodzielnie w przyrodzie, równy 1,60277∙10^-19 C
b) Ładunek cechuje się ziarnistością. Oznacza to, że jego wartość jest zawsze całkowitą wielokrotnością ładunku element. równego e
39.Zasada zachowania ładunku elektrycznego - zachowania zasada ładunku elektrycznego jest związana z niezmienniczością względem tzw. transformacji cechowania.
40.Prawo Coulomba - jedno z podstawowych praw elektrostatyki, określające siłę F wzajemnego oddziaływania (odpychania lub przyciągania) dwóch punktowych ładunków elektrycznych q₁ i q₂, odległych od siebie o r i znajdujących się w ośr. o przenikalności elektrycznej 
41.Natężenie pola elektrostatycznego. Ładunek próbny.
a) Natężenie pola elektrostatycznego E = lim F/q; E = k*(q/r²)_er
b) ładunek próbny - malutki ładunek dodatni (+)
c) Zasada Superpozycji - E= E₁ + E₂ + … + E_n
42.Linie sił pola elektrostatycznego (definicja, przykłady dla ładunków punktowych). Pole jednorodne
a)Siły elektrostatyczne działają wzdłuż linii pola
b)Styczna do linii sił pola w danym punkcie wyznacza kierunek wektora natężenia E w tym punkcie
c)Liczba linii na jednostkę przekroju poprzecznego jest proporcjonalna do wartości natężenia E=lim N/s
d)Pole jednorodne - Pole w którym siły w każdym punkcie działają ze stałą wartością (stałe natężenie)
43.Potencjał i powierzchnie ekwipotencjalne
a)Potencjał - Stosunek energii potencjalnej do ładunku obranego - φ= lim Ep(r) = k*q/r
b)Powierzchnie ekwipotencjalne - Powierzchnia stałego potencjału (nie zmienia się) φ=const. Linie pola są prostopadłe do powierzchni Ekwipotencjalnej.
44.Dipol elektryczny. Elektryczny moment dipolowy.
a)Dipol - zespół 2 blisko siebie położonych ładunków elektrycznych
b)Elektryczny moment dipolowy - p_e = q*a

c) Dipol elektryczny w jednorodnym  polu elektrycznym: F₊=F_- Para sił stara się obrócić dipol do polożenie równoległego do linii sił pola.
45.Strumień pola elektrycznego - Liczba linii sił pola przechodzących przez powierzchnię
a)Poprzeczną - Φ=E*S Nie poprzeczną - Φ=E*Scosα
46.Prawo Gaussa dla pola elektrycznego w próżni i w dielektrykach
a)Prawo Gaussa dla pola - strumień wektora indukcji elektrycznej D przez dowolną powierzchnię zamkniętą jest równy całkowitemu ładunkowi Q zawartemu w przestrzeni V ograniczonej tą powierzchnią: Φ=∫D*ds = ∫ρ*ds
b)Prawo Gaussa w Dielektrykach Φ=∫D*ds = Q_cał ∫ε₀εW*ds = Q_cał
47.Gęstość liniowa, powierzchniowa i objętościowa ładunku
a)Gęstość Liniowa - ρ = Q/V Gęstość Powierzchniowa - δ = Q/S
Gęstość Objętościowa - λ=Q/L
48.Dielektryki. Rodzaje dielektryków. Polaryzacja
a)Dielektryki - Nie przewodzą ładunków elektrycznych (Izolatory)
b) Polarne - molekuły posiadają trwały moment dipolowy (brak pola)
c) Niepolarne - nie ma momentu dipolowego. Pole zewnętrzne powoduje rozsunięcie ładunków
d)Polaryzacja - indukowany moment dipolowy p = lim Σ p_e/V p_e - suma momentów dipolowych w V

Natężenie pola elektr w dielektryku

E - wypadkowe pole elektryczne w dielektryku, E_o - zewnętrzne pole elektryczne przyłożone do dielektryka, ε - przenikalność elektryczna próżni, ε_r - przenikalność względna dielektryka.

49.Wektor indukcji elektrycznej (wektor przesunięcia)- D= ε_0*E + P= ε_0*E + ε_0*χ*E= ε₀(1+χ)E = ε_0*ε*E
50.Pole elektryczne na powierzchni i wewnątrz przewodnika
a)Na powierzchni przewodnika - E || ds; natężenie ↓ do powierzchni; E=0 ∫D*ds = Q_cał∫δ*ds
b)Wewnątrz przewodnika
51.Pojemność przewodnika. Pojemność kondensatora
a)Pojemność przewodnika - Q = C*φ C - Pojemność; φ - potencjał względem ∞
b)Pojemność kondensatora - Q = C*∆φ

52. Natężenie i gęstość prądu elektrycznego
a)Natężenie - ładunek przepływający przez przekrój poprzeczny przewodnika w jednostce czasu J = dq/dt
b)Gęstość prądu - ilość ładunku przepływająca przez jednostkę powierzchni w jednostce czasu
j = J/S J = j*s J = ∫j*ds.
53.Strumień pola magnetycznego. Prawo Gaussa dla pola magnetycznego
a)Strumień pola magnetycznego przechodzący przez powierzchnię zamkniętą równy jest ZERO
b)Prawo Gaussa dla pola magnetycznego - Φ=∫B*ds = 0 B - indukcja pola magnetycznego
54.Prawo Biota-Savarta - prawo określające wielkość i kierunek indukcji magnetycznej w dowolnym punkcie pola magnetycznego wytworzonego przez przewodnik z prądem elektrycznym
dH = (J/4Π)*[(dl x r)/r³]; dB = μ₀(J/4Π)*[(dl x r)/r³]
55.Siła Lorentza. Ruch naładowanej cząstki w polu magnetycznym
a)Siła Lorentza - siła F, z jaką pole elektromagnetycznej działa na poruszającą się cząstkę naładowaną: F = q₀(v × B), gdzie q — ładunek elektryczny cząstki, B — indukcja magnet.,
v — prędkość cząstki
b)Ruch naładowanej cząstki w polu magnetycznym: F_L=q(v × B) = dv/dt = v × qB/ω gdzie ω=qB/m a po okręgu v= ω × r

56.Działanie pola magnetycznego na przewodnik z prądem. Oddziaływanie dwóch równoległych przewodników z prądem
a) Działanie pola magnetycznego na przewodnik z prątem dF = J(dl x B) dl - długość przewodnika; B - wektor indukcja magnetyczna; J - natężenie prądu
57.Prawo Oersteda(ampera) (zastosowanie dla prostoliniowego przewodnika z prądem)
a)∫B*ds. = μ₀J (J = ↓J₁ - ↑J₂);( J = ↑J₁ + ↑J₂);( J = ↓J₁ + ↓J₂)
b)Dla próżni B = μ₀H H - natężenie pola magnetycznego
58.Rodzaje materiałów magnetycznych (pętla histerezy magnetycznej)
a)Diamagnetyki χ < 0 (złoto, srebro, miedz) Nadprzewodnik χ = -1 WYPYCHANY przez magnez
b)Paramagnetyki χ (małe) >0 (ciekły tlen, platyna, wolfram) WCIĄGANY przesz magnes
c)Ferromagnetyki χ (duże) > 0 (żelazo, nikiel, kobalt) Zależy od wewnętrznego pola magnetycznego. Występują domeny - obszary jednakowo namagnetyzowane
59.Indukcja elektromagnetyczna. Reguła Lenza
a)Siła Elektromotoryczna indukcji jest wprost proporcjonalna do szybkości zmian strumienia przechodzącego przez powierzchnię S
Є_ind = -dΦ_B/dt Є_ind - siła elektromotoryczna indukcji
b)Reguła Lenza - Obwód nie pozwala na zmiany. Reguła określająca kierunek prądu elektrycznego w obwodzie elektrycznym, powstającego przez indukcję elektromagnetyczną: kierunek prądu indukowanego jest zawsze taki, że jego pole magnetyczne przeciwdziała przyczynie, która go wywołała

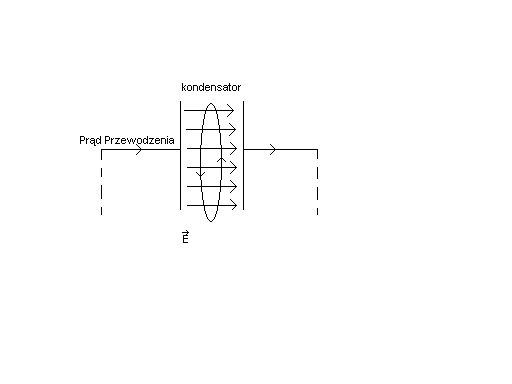
60.Prąd przesunięcia i prąd przewodzenia
a)Prąd przesunięcia - prąd elektryczny związany ze zmianami strumienia indukcji elektrycznej; występuje np. wewnątrz kondensatora umieszczonego w obwodzie prądu zmiennego
b)Prąd przewodzenia - Ukierunkowany ruch (przepływ) swobodnych ładunków elektrycznych w środowisku przewodzącym, pod wpływem pola elektrycznego
c)Uogólnione prawo Oersteda (Ampera) - ∫H*dl = J + J_przes = J + dΦ_D/dt
61.Równania Maxwella w postaci całkowej
a)I uogólnione prawo Faradaya:
∫E*dl = - dΦ_B/dt
E - natężenie pola elektrycznego; Φ_D = B*ds. - strumień indukcji pola magnetycznego
Zmienne pole magnetyczne wytwarza wirowe pole elektryczne które może wywołać prąd elektryczny
b)II uogólnione prawo Oersteda:
∫H*dl = J + J_przes = J + dΦ_D/dt dΦ_D = ∫D*ds.
H - natężenie pola magnetycznego; D - wektor indukcja pola elektrycznego; J - Prąd przewodzenia
Prąd elektryczny lub zmienne pole elektryczne, wytarza wirowe pole magnetyczne
c)III Prawo Gaussa dla pola Elektrycznego:
Φ_D = ∫D*ds. = Q_cał = ∫δ*ds
D - wektor indukcja pola elektrycznego; Q_cał - całkowita ilość ładunku powierzchni; δ - gęstość pow.
Strumień indukcji elektrycznej przez dowolną powierzchnię zamkniętą jest równy całkowitemu ładunkowi zawartemu wewnątrz tej powierzchni
d)IV Prawo Gaussa dla pola Magnetycznego:
Φ_B = ∫B*ds. = 0 Równanie Materiałowe - D = ε₀*ε*E B = μ₀*μ*H B - indukcja pola magnetycznego
e)Strumień indukcji pola magnetycznego przez dowolną powierzchnię zamkniętą jest równy ZERO
f)Nie istnieje w przyrodzie monopol magnetyczny
g)Linie strumienia indukcji magnetycznej są krzywymi zamkniętymi

1

---