Obiektem badań jest przenośnik taśmowy, w którego pracy mogą wystąpić awarie następujących typów:
Mechaniczne (zmienne z tym typem awarii oznaczane są jako Xm. lub X1)
Elektryczne (Xe lub X2)
Taśmy (Xt lub X3)
Górnicze (Xg lub X4)
Czasy poprawnej pracy i usuwania awarii są wykładnicze.
Znając intensywność powstawania poszczególnych typów awarii: λm., λe, λt, λg i średnie czasy usuwania awarii: Tam, Tae, Tat, Tag możemy wyznaczyć:
Średni czas poprawnej pracy przenośnika
![]()
gdzie:
λ1 = 0,0015
λ2 = 0,0033
λ3 = 0,0005
λ4 = 0,0427
λz = Σ λi = 0,048
Tśr=20,83
Średni czas usuwania awarii przenośnika
![]()
gdzie:
![]()
![]()
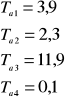
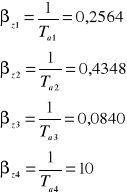
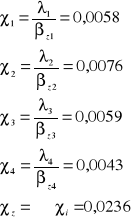
![]()
![]()
0,4917
Prawdopodobieństwo, że przenośnik jest zdatny w każdej chwili
![]()
gdzie:
χ = χz = 0,0236
K = 0,9769
Prawdopodobieństwo, że przenośnik zdatny na początku zmiany przepracuje zmianę bezawaryjnie
![]()
gdzie:
K = 0,9769
t0 = 8 h; czas bezawaryjnej pracy (czas trwania 1 zmiany)
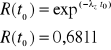
![]()
Prawdopodobieństwo, że przenośnik zdatny na początku zmiany będzie zdatny na końcu zmiany
![]()
gdzie:
K = 0,9769
t = 8 h
βz = 2,0339
λz = 0,0026
![]()
Prawdopodobieństwo, że przenośnik zdatny na początku zmiany będzie zdatny na końcu zmiany i przepracuje bezawaryjnie następną zmianę
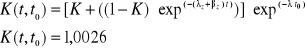
Dla szeregowego ciągu złożonego z trzech przenośników wyznaczyć:
Średni czas poprawnej pracy ciągu przenośników
![]()
gdzie:
λz = 0,048
λz1 = 3 ∙ λz
![]()
Średni czas usuwania awarii ciągu przenośników
![]()
gdzie:
βz1 = βz = 2,0339
![]()
Prawdopodobieństwo, że ciąg przenośników jest zdatny w dowolnej chwili
![]()
gdzie:
λz1 =
βz1 =
![]()
K= 0,9769
Średni sumaryczny czas poprawnej pracy ciągu przenośników w ciągu doby
![]()
gdzie:
t = 24
K = 0,9769
![]()
Średnia liczba odnów w ciągu przenośników w doby
![]()
gdzie:
t = 24
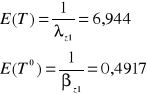
![]()
Przyjmując średni czas poprawnej pracy wentylatora Tp i średni czas usuwania awarii Ta oraz nieograniczoną odnowę dla dwuelementowej i trójelementowej stacji wentylatorowej (rezerwa nieobciążona, k elementów roboczych, 1 element rezerwowy) wyznaczyć:
Gotowość
Stacja dwuelementowa
![]()
gdzie:
k = 1
Tp = 3531,5
Ta = 24,0
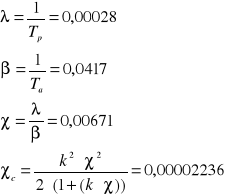
K = 0,99997763
Stacja trójelementowa
![]()
gdzie:
k = 2
Tp = 3531,5
Ta = 24,0
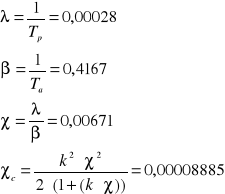
K=0,99991115
Średni czas poprawnej pracy stacji
Stacja dwuelementowa
![]()
gdzie:
k = 1
χ = 0,00671
λ = 0,0028
T=53939,75
Stacja trójelementowa
![]()
gdzie:
k = 2
χ = 0,00671
λ = 0,0026
T = 14714,55
Średni czas awarii stacji
Stacja dwuelementowa
![]()
gdzie:
β = 0,4167
![]()
Stacja trójelementowa
![]()
gdzie:
β = 0,4167
![]()
Wyszukiwarka
Podobne podstrony:
dałkowski, W10- mechaniczny
dałkowski, W10- mechaniczny
dałkowski, W10- mechaniczny
choroszy, W10- mechaniczny
janus, W10- mechaniczny
janus, W10- mechaniczny
zamonik, W10- mechaniczny
zamonik, W10- mechaniczny
biernacki, W10- mechaniczny
wilczewski, W10- mechaniczny
Baszczuk, W10- mechaniczny
cholewa, W10- mechaniczny
pękalski, W10- mechaniczny
Baszczuk, W10- mechaniczny
Baszczuk, W10- mechaniczny
Iwko, W10- mechaniczny
janus, W10- mechaniczny
pękalski, W10- mechaniczny
więcej podobnych podstron