Zagadnienia na egzamin

1. Model sferyczny ciała stałego. Defekty w ciele stałym.

2. Naprężenia w ciele stałym.

3. Gęstość liniowa i powierzchniowa atomów.

4. Ciepło właściwe klasycznego ciała stałego.

5. Temperaturowa zależność ciepła właściwego

6. Rozszerzalność cieplna ciał stałych

7. Pasma energetyczne. Metale, półprzewodniki i izolatory

8. Klasyczna teoria przewodnictwa metali

9. Półprzewodnik typu n.

10. Półprzewodnik typu p.

11. Złącze p-n.

12. zależność temperaturowa przewodnictwa

elektrycznego półprzewodników

13. Fotoprzewodnictwo

14. Magnetyczne właściwości ciał stałych, diamagnetyzm i paramagnetyzm.

Orbitalny moment magnetyczny, wpływ pola magnetycznego na ruch

orbitalny elektronu. Spinowy moment magnetyczny .

15. Ferromagnetyzm, domeny ferromagnetyczne.

Antyferromagnetyzm i ferrimagnetyzm

Gęstość liniowa i gęstość powierzchniowa

Liniowa gęstość jest określona jako liczba atomów na jednostkę długości, których środki leżą na wektorze kierunkowym wybranego kierunku krystalograficznego.

w ogólności

r - odległość pomiędzy środkami sąsiednich atomów.

Gęstość powierzchniowa jest to liczba atomów na jednostkę powierzchni, których środki leżą na wybranej płaszczyźnie krystalograficznej.

Dyslokacja krawędziowa - wektor Burgersa

Dodatkowa półpłaszczyzna atomów.

Linia dyslokacji.

Zniekształcenie sieci krystalicznej w obszarze wokół tej linii. Wielkość tego odkształcenia zmniejsza się wraz z odległością od linii dyslokacji. W dalekiej odległości sieć krystaliczna jest już idealna. Dyslokacja krawędziowa - symbol _┴ (+).

Dodatkowa półpłaszczyzna która jest wbudowana w dolnej części kryształu:

┬ (-).

Wielkość i kierunek zniekształcenia sieci krystalicznej - wektor Burgersa

Dla metali o strukturze ściśle upakowanej wartość tego wektora jest równa jednej odległości międzyatomowej.

Naprężenie rozciągające (ściskające)

odkształcenie (wydłużenie lub skrócenie)

^lub

Odkształcenie sprężyste

Prawo Hooke'a

lub

gdzie E - moduł Younga (moduł sprężystości podłużnej).

Odkształcenie poprzeczne - zwężenie lub poszerzenie.

W zakresie, w którym prawo Hooke'a jest spełnione:

lub

ν - liczba Poissona

- „minus” oznacza, że ε i ε_p mają przeciwne znaki

Naprężenie ścinające

Stan naprężeń

Naprężenie normalne σ_α i naprężenie styczne τ_α

Zależność ciepła właściwego od temperatury dla metali

W wysokich temperaturach ciepło właściwe przyjmuje niemal stałą wartość wynoszącą około 25 J/molK.

„zredukowana” skala temperatur, czyli w funkcji T/θ_D.

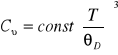
Prawo jest spełnione w zakresie temperatur

Temperatura Debye'a.

W tej temperaturze ciepło właściwe osiąga wartość wynoszącą około 96 % wartości maksymalnej.

v_D - charakterystyczna maksymalna dla danego ciała częstość drgań

h - stała Plancka

k - stała Boltzmana

Przyjmujemy, że v_D jest równe częstości v uzyskanej ze wzoru:

Rozszerzalność cieplna ciał stałych

l = l₀(1+ α∆T)

l = l₀+ l₀ α∆T)

l - l₀ = l₀ α∆T)

∆l = l₀ α∆T

α = ∆l/l₀∆T [α]=1/K

α - współczynnik rozszerzalności liniowej

Rozszerzalność powierzchniowa

l = l₀(1+ α∆T)

a powierzchnia S = l²

ponieważ α <<1 wyraz (α∆T)² można pominąć

γ = 2α - współczynnik rozszerzalności

powierzchniowej

Rozszerzalność objętościowa

l = l₀(1+ α∆T)

objętość sześcianu V = l³

ponieważ α <<1 wyraz (3α∆T)² i (α∆T)³ można pominąć.

β = 3α - współczynnik rozszerzalności

objętościowej

Struktura pasmowa - metale, półprzewodniki, półprzewodniki domieszkowane.

Metale

Przewodzenie prądu przez metale.

Metal przewodzi prąd, ponieważ elektrony w niewypełnionym paśmie walencyjnym mogą przechodzić do wyższych stanów energetycznych istniejących w tym samym paśmie. Energia elektronów o najwyższej energii ruchu translacyjnego w temperaturze zera bezwzględnego nosi nazwę energii Fermiego E_F.

Poziom ten rozgranicza poziomy wszystkie poziomy (stany) zapełnione od poziomów (stanów) pustych.

Izolatory

W przypadku izolatorów również mamy do czynienia ze strukturą pasmową, ale pasmo walencyjne jest całkowicie wypełnione elektronami. Elektrony nie mogą więc poruszać się wewnątrz pasma pod wpływem pola elektrycznego. Poziomy nieobsadzone znajdują się w paśmie wyższym. Jednakże aby elektron mógł przejść do wyższego pasma musi mieć energię wystarczającą do pokonania dużej przerwy energetycznej E_g oddzielającej pasmo obsadzone od nieobsadzonego. W przypadku diamentu ta różnica energetyczna wynosi około 5,5 eV. W zasadzie żaden elektron nie może pokonać tak dużej przerwy. Dlatego diament jest dobrym izolatorem.

Półprzewodnik

Pasmo walencyjne jest całkowicie wypełnione. Szerokość przerwy energetycznej E_g, w półprzewodniku jest znacznie mniejsza niż w izolatorze. W przypadku krzemu E_g = 1,1 eV a więc jest to półprzewodnik. W przypadku półprzewodnika wyróżniamy: pasmo walencyjne i pasmo przewodnictwa. Drgania termiczne - przejście pewnej liczby elektronów z pasma walencyjnego do pasma przewodnictwa i tym samym przewodzenie elektryczności (ruch ładunków -nośników- po przyłożeniu różnicy potencjałów). Nośniki ładunków w krzemie w paśmie przewodnictwa - elektrony w oraz dziury w paśmie walencyjnym. Dziury nieobsadzone stany energetyczne w paśmie walencyjnym.

Nośniki ładunku - elektrony i dziury.

Półprzewodniki domieszkowane

Wprowadza się zwykle na każde 10⁷ atomów krzemu 1 atom domieszki, który zastępuje w sieci atom krzemu. Istnieją dwa typy domieszkowania:

typ n i typ p.

Struktura elektronowa atomu krzemu: 1s²2s²2p⁶3s²3p² - 14 elektronów

Prędkość efektywna i prędkość unoszenia.

Elektron doznający przyspieszenia uzyskuje w czasie pomiędzy zderzeniami prędkość υ_τ .

τ - średni czas pomiędzy zderzeniami

Prędkość ta zmienia się więc od wartości 0 do υ_τ. Średnia prędkość nosi nazwę prędkości unoszenia i oznaczamy ją jako υ_d.

υ_d ≈ 10^-13 υ_ef υ_ef ≈ 1,6·10⁶ m/s.

Dlaczego w przypadku metali spełnione jest prawo Ohma.

Dlaczego w przypadku metali spełnione jest prawo Ohma.

Ruchliwość elektronów:

Ilość stanów w jednostce objętości o energiach z przedziału od E do E + dE - g(E)dE;

g(E) - gęstość stanów dla energii E. Jednostką wielkości g(E)dE jest liczba stanów na metr sześcienny [m^-3]. Jednostką gęstości stanów g(E) jest liczba stanów ma metr sześcienny na elektronowolt [m^-3∙eV^-1].

Wykres tej funkcji

Funkcja rozkładu energii Fermiego-Diraca:

Ze wzoru widać, że prawdopodobieństwo zależy od różnicy E - E_F. Różnica ta może być dodatnia lub ujemna.

Jeśli T = 0 to dla E - E_F < 0 e^(E-EF)/kT= e^-∞ = 0

i f(E) = 1

Jeśli T = 0 to dla E - E_F > 0 to e^(E-EF)/kT = e^+∞ i f(E) = 0

Dla temperatur wyższych część elektronów o energiach mniejszych od energii Fermiego przechodzi do stanów o energiach niewiele większych od energii Fermiego.

Jeśli energia E = E_F to w każdej temperaturze czynnik e^(E-EF)/kT = e⁰ = 0 i f(E_F)=0,5.

Energia Fermiego jest energią stanu kwantowego, który jest obsadzony przez elektron z prawdopodobieństwem 0,5.

Gęstość stanów obsadzonych N(E)

- iloczyn gęstości stanów g(E) i prawdopodobieństwa obsadzenia tych stanów f(E):

N(E) = g(E)∙f(E)

Zależność przewodnictwa od temperatury

- półprzewodnik samoistny:

Energia aktywacji w tym wzorze wynosi

Wyznaczanie energii aktywacji i E_g.

Pomiar przewodnictwa w funkcji temperatury:

Przewodnictwo silnie zależy od temperatury.

Dla T = 0 nie ma elektronów w paśmie przewodnictwa.

Przewodniki domieszkowe

W przypadku półprzewodników domieszkowanych liczby dziur (N_p) i elektronów (N_e) są różne. Energia Fermiego w przypadku półprzewodników typu n jest bliska energii poziomu donorowego a w przypadku półprzewodników typu p bliska energii poziomu akceptorowego.

Półprzewodniki samoistne

Przewodnictwo silnie zależy od temperatury.

Dla T = 0 nie ma elektronów w paśmie przewodnictwa.

Wzrost temperatury powoduje zwiększenie liczby elektronów w tym paśmie i wzrost przewodnictwa.

W przypadku półprzewodników domieszkowych całkowite przewodnictwo będzie związane z przewodnictwem domieszek i przewodnictwem samoistnym.

lub

Niskie temperatury

- przewodnictwo samoistne małe

- przewodnictwo domieszkowe znacznie większe

Wysokie temperatury

- przewodnictwo samoistne duże

- przewodnictwo domieszkowe znacznie mniejsze

Fotoprzewodnictwo

Półprzewodniki nie poddawane działaniu światła.

Prąd „ciemny” - opór „ciemny”

Półprzewodniki naświetlane odpowiednio dobranym rodzajem promieniowania.

Obserwacja - skokowy wzrost natężenia prądu płynącego w obwodzie.

Fotoprąd - I_f

różnica prądu płynącego w przypadku półprzewodnika nieoświetlonego i oświetlonego.

Obserwowane zjawisko - fotoprzewodnictwo.

Półprzewodniki samoistne

Promieniowanie o energii kwantów równych lub przewyższających E_g powoduje przeniesienie elektronów z pasma walencyjnego do pasma przewodnictwa.

Generowanie par elektron-dziura.

Dodatkowe nośniki prądu - wzrost przewodnictwa właściwego, zmniejszenie oporu i wzrost prądu. Przewodniki samoistne - częstość progowa

Półprzewodniki domieszkowe

Półprzewodniki typu n

Częstość progowa

Półprzewodniki typu p

Częstość progowa

Zjawisko fotoprzewodnictwa

- zjawisko fotoelektryczne wewnętrzne

Energia dostarczona do półprzewodnika jest „zmagazynowana” jako przeniesienia elektronów na wyższy poziom energetyczny (do pasma przewodnictwa).

Złącze p-n dioda

Złącze p-n (zjawiska kontaktowe)

Jeden obszar kryształu domieszkujemy na typ n a sąsiedni obszar na typ p.

Płaszczyzna złącza.

Ruch nośników większościowych

Elektrony w obszarze typu n, znajdujące się blisko płaszczyzny złącza będą dyfundować przechodząc do obszaru p, gdzie jest niewiele elektronów. Ruch elektronów i dziur - prąd dyfuzji I_dyf, który jest skierowany z lewa na prawo (od p do n).

W pobliżu płaszczyzny złącza pojawią się więc nieruchome ładunki dodatnie. Elektron, który przedyfundował do obszaru p zrekombinuje ze zjonizowanym atomem akceptora, co jest równoznaczne z pojawieniem się nieruchomych ładunków ujemnych w obszarze p.

W wyniku dyfuzji powstanie po obydwu stronach złącza ładunek przestrzenny

Ruch ładunków większościowych (elektronów i dziur) powoduje więc wytworzenie dwóch obszarów ładunku przestrzennego (dodatniego i ujemnego). Te dwa obszary tworzą tzw. obszar zubożony, którego nazwa wynika z faktu, że znajduje się tam niewiele ruchomych nośników ładunku.

Szerokość obszaru zubożonego - d_o.

Kontaktowa różnica potencjałów V_o. Ta różnica potencjałów hamuje dalszą dyfuzję elektronów i dziur.

Ruch nośników mniejszościowych

Różnica potencjałów stanowi barierę dla nośników większościowych. Jednakże w części p i w części n mamy również nośniki mniejszościowe. Ruch nośników mniejszościowych

- prąd unoszenia (prąd dryfowy) I_dryf.

W równowadze wypadkowy prąd jest równy zero.

Tranzystor

Magnetyzm

B_o = μ_oH

B = B_o + μ_oM = μ_oH + μ_oM = μ_o(H + M) = μ_oμ_rH

μ = μ_rμ_o

B = μH= μ_rμ_oH

Paramagnetyki

Paramagnetyzm

Materiały posiadające niesparowane elektrony

- moment magnetyczny rzędu magnetonu Bohra. Wypadkowe namagnesowanie w nieobecności zewnętrznego pola magnetycznego wynosi 0.

Działanie pola magnetycznego:

- na każdy moment magnetyczny działa moment siły, który ustawia ten moment w pozycji o najmniejszej energii potencjalnej.

Materiał wewnątrz cewki, która wytwarza indukcję B_o.

Pojawienie się magnetycznego momentu dipolowego w materiale

- namagnesowanie lub magnetyzacja (M).

Moment magnetyczny przypadający na jednostkę objętości nosi nazwę namagnesowania (M) .

Indukcja występująca w materiale wynosi wtedy:

B = B_o + μ_oM lub B = μ_oH + μ_oM

μ_o - przenikalność magnetyczna próżni

Inne wielkości charakteryzujące magnetyczne właściwości materiałów:

- przenikalność magnetyczna μ

- względna przenikalność μ_r

Związek pomiędzy tymi wielkościami :

μ = μ_rμ_o

B = μH= μ_rμ_oH

Zależność namagnesowania (M) od natężenia zewnętrznego pola magnetycznego :

M = χ_mH

χ_m - podatność magnetyczna

χ_m = μ_r-1

Materiały paramagnetyczne.

Zależność podatności magnetycznej w funkcji temperatury - prawo Curie:

C - stała charakterystyczna dla danego materiału magnetycznego.

Paramagnetyzm elektronów swobodnych, który jest niezależny od temperatury.

Ferromagnetyki

Istnieją materiały (żelazo, nikiel, kobalt), w których oddziaływania momentów magnetycznych elektronów (niesparowanych) prowadzą do ich wzajemnego równoległego uporządkowania i pojawienia się namagnesowania spontanicznego. Jest to porządkowanie ferromagnetyczne.

Materiały ferromagnetyczne - ferromagnetyki.

Dla większości ferromagnetyków istnieje pewna temperatura zwana temperaturą Curie -T_c poniżej której materiał jest ferromagnetyczny a powyżej której materiał zachowuje się tak jak paramagnetyk.

Przemiana fazowa paramagnetyk - ferromagnetyk.

Zależność podatności magnetycznej od temperatury.

Prawo Curie-Weissa :

- temperatura Curie

Właściwości ferromagnetyczne są związane z uporządkowaniem spinowych momentów magnetycznych.

Własności ferromagnetyczne pojawiają się u pierwiastków, których podpowłoki wewnętrzne są niezapełnione (żelazo, kobalt, nikiel).

Domeny ferromagnetyczne. Obszary, w których (namagnesowanie) magnetyzacja ma określony kierunek, ale inny niż w obszarach sąsiadujących. Obszary te nazywamy domenami. Ściany lub granice domenowe. Struktura domenowa.

Działanie pola magnetycznego zewnętrznego powoduje zmianę struktury domenowej i ruch granic.

Działanie silnych pół - zjawisko nasycenia namagnesowania. Wektor namagnesowania ma jeden kierunek w całej próbce.

W materiałach ferromagnetycznych zależność magnetyzacji od pola zewnętrznego jest inna przy wzroście i zmniejszaniu się pola magnetycznego. Zjawisko histerezy (pętle histerezy), pole koercji:

Klasyfikacja materiały ferromagnetycznych

• materiały magnetycznie miękkie - małe pole koercji

• materiały magnetycznie twarde - duże pole koercji. Materiały miękkie magnetycznie

1

---