4EKRAN_151
Lekcja 7
Obwody nieliniowe prądu stałego
W lekcji czwartej przedstawiono problematykę związaną z obwodami nieliniowymi. Na początku omówiono zależność rezystancji przewodników od temperatury. Zaprezentowano sposób tworzenia charakterystyk wypadkowych dla elementów połączonych szeregowo i równolegle. Szereg przykładów przedstawia zasady analizy obwodów nieliniowych prądu stałego.
4EKRAN_152
Zależność rezystancji od temperatury
Rezystancja ciał jednorodnych jest przy danych rozmiarach geometrycznych proporcjonalna do ich rezystywności, która zależy od temperatury, wilgotności, naświetlenia, pola magnetycznego i elektrycznego.
Rozwijając funkcję temperatury w szereg Taylora i biorąc dwa pierwsze wyrazy mamy:
![]()
(1)
Przyjmijmy następujące podstawienie:
![]()
Wówczas otrzymamy:
![]()
Komentarz-EKRAN_152
Współczynnik![]()
nazywamy współczynnikiem temperaturowym w temperaturze to
Współczynnik ten najczęściej określa się dla temperatury ![]()
.
4EKRAN_153
Jeżeli przyjmiemy temperaturę odniesienia t0=200 C to rezystancję w funkcji temperatury określa się wzorem:
![]()
(2)
Dla miedzi współczynnik temperaturowy w temperaturze 20 0C ma wartość: ![]()
Dzieląc powyższe równanie (2) przez l/s otrzymamy zależność rezystywności od temperatury (uważa się za pomijalny fakt zmiany geometrycznej metalu)
![]()
(3)
Komentarz-EKRAN_153
W rzeczywistości metal ze wzrostem temperatury zwiększa swoją objętość, ale stosunek długości do powierzchni l/S w dwóch różnych temperaturach nie musi być zachowany. Pomimo tego uznaje się, że wzór (2) jest proporcjonalny do (3) a wynikające stąd przybliżenie jest mniejsze od faktu ograniczenia się w rozwinięciu szeregu Taylora do dwóch wyrazów.
4EKRAN_154
Dla większej dokładności niekiedy uwzględnia się trzeci wyraz rozwinięcia szeregu Taylora. Wówczas funkcja rezystancji przyjmuje postać.
![]()
![]()
Powyższe wzory można wykorzystywać z wystarczającą dokładnością dla obliczenia rezystancji metali w zakresie temperatur ![]()
Komentarz-EKRAN_154
W przypadku niektórych metali np. takich jak wolfram dla uzyskania satysfakcjonującej dokładności należy użyć wzoru na R(t) uwzględniającego współczynnik ![]()
. Zakres temperaturowy może być także większy.
4EKRAN_155
Przykład
Rezystancja zimnej cewki miedzianej o temperaturze 100C wynosi 10 . Po wyłączeniu zasilania zmierzono rezystancję ponownie i wyniosła 12 Obliczyć temperaturę końcową cewki przyjmując, że 20=0.004 1/K
Wykorzystując wzór określający rezystancję przewodu w funkcji temperatury możemy sformułować dwa wzory:
![]()
![]()
Dzieląc powyższe równania stronami eliminujemy nieznaną rezystancję R20 i otrzymujemy równanie z jedną niewiadomą tx.
Odpowiedź: Szukana temperatura wyniosła 580C.
4EKRAN_156
Elementy nieliniowe w obwodach prądu stałego.
Charakterystyka prądowo-napięciowa
Komentarz-EKRAN_156
Charakterystyki elementów nieliniowych mogą być przedstawione jako prądowo-napięciowe lub napięciowo-prądowe. Klasycznym przykładem elementu nieliniowego o niesymetrycznej charakterystyce jest dioda.
4EKRAN_157
Charakterystyka napięciowo-prądowa
Komentarz-EKRAN_157
Jeżeli charakterystyka elementu nieliniowego jest symetryczna względem początku układu to znaczy, że polaryzacja napięcia nie ma wpływu na rezystancję statyczną tego elementu.
4EKRAN_158
Definicja rezystancji statycznej i dynamicznej
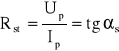
![]()
Komentarz-EKRAN_158
Rezystancja statyczna w danym punkcie pracy jest stosunkiem napięcia do prądu w tym punkcie. W geometrycznej interpretacji jest to tangens kąta nachylenia siecznej przechodzącej przez ten punkt i początek układu. Rezystancję dynamiczną definiujemy jako pochodną funkcji nieliniowej w tym punkcie, czyli jest to tangens kąta nachylenia stycznej do charakterystyki w rozpatrywanym punkcie pracy.
4EKRAN_159
Równoległe połączenie elementów nieliniowych.
Komentarz-EKRAN_159
Dwójnik zastępczy dwóch równolegle połączonych elementów charakteryzuje się tym, że przy danym napięciu, prąd przez niego płynący jest sumą prądów płynących w tych elementach. Tą własność wykorzystuje się przy tworzeniu charakterystyki zastępczej.
4EKRAN_160
Szeregowe połączenie elementów nieliniowych.
Komentarz-EKRAN_160
Analogicznie jak dla połączenia równoległego w celu wyznaczenia charakterystyki zastępczej dwóch szeregowo połączonych elementów należy narysować proste poziome ( w przypadku charakterystyki prądowo-napięciowej) i wzdłuż nich zaznaczać punkty wypadkowej charakterystyki dodając odpowiednie napięcia.
3EKRAN_161
Podstawowa metoda graficzna wyznaczania punktu pracy.
![]()
Komentarz-EKRAN_161
Równanie z II Prawa Kirchhoffa można zamienić na dwa z których pierwsze to równanie charakterystyki źródła napięciowego, a drugie charakterystyki elementu nieliniowego. Stąd punkt przecięcia tych charakterystyk wyznacza nam punkt pracy.
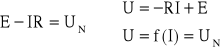
4EKRAN_162
Metody analityczne.
II prawo Kirchhoffa
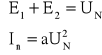
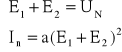
![]()
- analityczna charakterystyka elementu nieliniowego
Komentarz-EKRAN_162
W przypadku gdy znamy analityczną postać charakterystyk elementów nieliniowych, możemy dla danego obwodu sformułować układ równań np. na podstawie praw Kirchhoffa. Układ ten będzie układem nieliniowym stąd może nie istnieć jego analityczne rozwiązanie.
4EKRAN_163
Czy obwód nieliniowy można rozwiązać metodą superpozycji?.
Komentarz-EKRAN_163
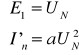
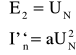
![]()
![]()
![]()
Porównując rozwiązanie obwodu z wszystkimi źródłami z rozwiązaniem otrzymanym metodą superpozycji widać niezgodność wyników.
WNIOSEK: Zasady superpozycji nie można stosować w obwodach nieliniowych!
4EKRAN_164
Przykład 4.1
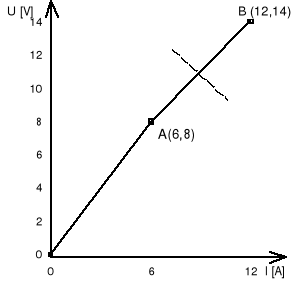
Zastąpić element nieliniowy dwójnikiem liniowym przy założeniu że punkt pracy będzie na przecięciu z odcinkiem AB. Następnie dobrać Rw jeżeli punkt pracy będzie środkiem odcinka AB, a E=18 V.
Komentarz-EKRAN_164
Na odcinku AB charakterystyka rezystora nieliniowego jest liniowa, a napięcie oraz prąd na tym rezystorze spełniają równanie prostej przechodzącej przez punkty A i B:
![]()
Podstawiamy do równania wartości odpowiadające punktom A i B na wykresie i rozwiązujemy układ równań:
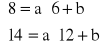
![]()
Zatem prąd i napięcie na rezystorze nieliniowym (gdy punkt pracy leży na odcinku AB) spełniają równanie:
![]()
(4.1)
gdzie:E`=2V, oraz R`=1![]()
.
4EKRAN_165
W takiej sytuacji element nieliniowy można zastąpić następującym dwójnikiem liniowym (rys.4.3)
Wówczas możemy rozważać nasz obwód jako liniowy:
Komentarz-EKRAN_165
Gdyby Rw było dane, to znalezienie punktu pracy sprowadzałoby się do rozwiązania obwodu z rys.4.4 przy założeniu, że znaleziony punkt znajdowałby się na półprostej AB. W przeciwnym razie należałoby element nieliniowy zastąpić rezystorem odpowiadającym charakterystyce do punktu A.
4EKRAN_166
W rozpatrywanym przypadku punkt pracy jest pośrednio podany (połowa odcinka AB). Stąd prąd płynący przez element nieliniowy można określić z wykresu I=9A. Formułując równanie Kirchhoffa dla obwodu z rys.4.4 otrzymamy:
E-E`-IR`-IRw = 0 stąd Rw=![]()
Odp. Parametry dwójnika liniowego zastępującego rezystor nieliniowy to E'= 2 V, R=1 , a rezystancja Rw gdy punkt pracy znajduje się na środku odcinka AB wynosi Rw=![]()
.
4EKRAN_167
Przykład.4.2
Na rys.4.5 przedstawiono schemat zastępczy obwodu z jednym połączonym równolegle elementem nieliniowym. Wyznaczyć napięcie oraz prąd płynący przez ten element. Charakterystyka elementu nieliniowego RN przechodzi przez punkty opisane w tab. 1 i jest przedstawiona na rys.4.6:
Rys. 4.5
Dane do obwodu z rys.4.6:
R1 = 5 [ Ω ], R2 = 5 [ Ω ], E1 = 10 [ V ], I2 = 2 [ A ].
4EKRAN_168
Komentarz-EKRAN_168
Rozwiązanie:
a ) Aby rozwiązać powyższe zadanie można zwinąć obwód do tzw. dwójnika aktywnego. W tym celu źródło napięciowe zamienimy na źródło prądowe ( Rys. 4.7 ).
4EKRAN_169
![]()
4EKRAN_170
b ) Następnie zwijamy wszystkie połączone równolegle rezystancje i SPM, aby otrzymać jedno źródło prądowe i jedną równolegle połączoną rezystancję (rys.4.8).
Komentarz-EKRAN_170
Parametry zastępczego dwójnika prądowego wynoszą:
![]()
![]()
4EKRAN_171
c ) W końcu przekształcono rzeczywiste źródło prądowe na źródło napięciowe ( Rys. 4.9).:
![]()
Z rys.4.9 wyznaczamy zależność napięcia UN na elemencie nieliniowym RN od prądu IN płynącego przez ten element:
![]()
=> ![]()
Komentarz-EKRAN_171
Równanie zależności napięcia UN od prądu IN wraz z charakterystyką elementu nieliniowego daje układ równań:
![]()
![]()
Aby otrzymać graficznie punkt pracy powyższą prostą wykreślono na tle charakterystyki elementu nieliniowego (rys.4.10). Graficzne wyznaczenie punktu pracy (punkt A) pozwala określić, którą część łamanej należy zastąpić równaniem liniowym, w celu analitycznego wyznaczenia rozwiązania.
4EKRAN_172
Równanie prostej przechodzącej przez punkty ( 1 ; 4 ) i ( 3 ; 6 ) ma postać:
![]()
Zatem analityczne znalezienie punktu pracy będzie rozwiązaniem układu równań:
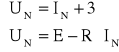
IN = 2 [ A ]
UN = 5 [ V ].
4EKRAN_173
Rys.4.10
Odpowiedź: Prąd i napięcie na elemencie nieliniowym wynoszą: IN = 2 [ A ], UN = 5 [ V ].
Komentarz-EKRAN_173
W powyższym przykładzie ze względu na aproksymację charakterystyki łamaną, można było wyznaczyć dokładne analityczne rozwiązanie. W przypadku gdy mamy charakterystykę elementu nieliniowego daną w postaci krzywej możemy w analogiczny sposób zastosować metodę przecięcia się charakterystyk. Jednak w przypadku obwodu z kilkoma elementami nieliniowymi musimy aproksymować lub interpolować charakterystyki i wówczas można rozwiązywać układ równań nieliniowych sformułowanych na podstawie praw Kirchhoffa.
Przykład rozwiązania takiego obwodu rozwiązanego w środowisku Mathcad przedstawiono na następnych ekranach.
4EKRAN_174
Rozwiązanie obwodu elektrycznego z elementami nieliniowymi w programie Mathcad przy wykorzystaniu gotowych procedur interpolacyjnych.
Wyznaczyć rozpływ prądów w układzie na rysunku 4.11, mając dane charakterystyki elementów nieliniowych I(u) oraz J(u), oraz podane parametry pozostałych elementów obwodu: E=5 [V]; Iz=0.5 [A]; R1=1 [Ω].
Rys.4.11. Schemat obwodu z elementami nieliniowymi
Komentarz-EKRAN_174
Poniższy przykład rozwiązano określając funkcje interpolujące dwiema metodami tj. z wykorzystaniem procedur linterp oraz interp. Ze względu na zbadanie stopnia dokładności rozwiązania obwodu przy użyciu powyższych procedur, interpolowane funkcje były dane i zostały na końcu wykorzystane do rozwiązania „dokładnego”.
4EKRAN_175
Start Programu
Dane obwodu:
![]()
![]()
![]()
Zdefiniowanie indeksu tablicy
![]()
![]()
![]()
Podanie wartości kolejnych wyrazów wektorów dla funkcji: I(u)=![]()
; J(U)=![]()
Charakterystyki elementów nieliniowych I(u) oraz J(u) podane w postaci tabel
![]()
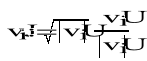
Komentarz-EKRAN_175
W celu uzyskania symetrycznych charakterystyk, funkcje analityczne zostały pomnożone przez wyrażenie: funkcja dzielona przez jej moduł. Wykorzystywana jest cecha programu Mathcad, w którym 0/0=0.
4EKRAN_176
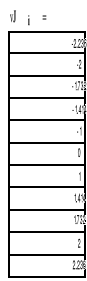
Punkty charakterystyk nieliniowych danych w postaci wektorów danych:



Komentarz-EKRAN_176
W przypadku gdy chcemy wpisać dane pomiarowe po wpisaniu nazwy musimy użyć znaku definicji := i wpisać pierwszą wartość, a następnie kliknąć przecinek. Wówczas pojawi się miejsce na wpisanie następnego pomiaru.
4EKRAN_177
Procedura interpolacji liniowej funkcji
![]()
![]()
![]()
![]()
Procedura interpolacji wielomianami sześciennymi funkcji
![]()
![]()
![]()
![]()
Komentarz-EKRAN_177
Dzięki użyciu funkcji "linterp" (interpolacja liniowa) i funkcji "cspline" (interpolacja wielomianami sześciennymi) program powoduje, że nieanalityczne charakterystyki I(u) i J(U)
stają się analityczne w całej swojej dziedzinie. Dzięki temu możliwe jest rozwiązanie badanego obwodu.
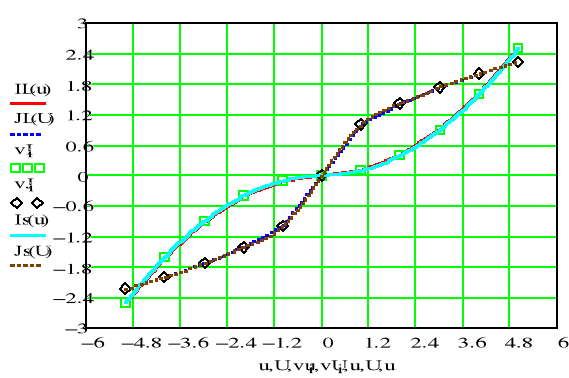
Rys.1. Wykresy przedstawiające przebiegi funkcji otrzymanych w wyniku interpolacji procedurą linterp (IL(u),JL(U)), oraz interp (Is(u),Js(U))
4EKRAN_178
W celu rozwiązania układu równań nieliniowych przedstawionych poniżej, zgodnie z wymogiem procedury numerycznej, przypisujemy poszukiwanym wielkościom wartości startowe:
Start programu
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Układ równań opisujących obwód z elementami nieliniowymi.
![]()
![]()
![]()

Komentarz-EKRAN_178
Zastosowanie funkcji "Find" powoduje rozwiązanie zdefiniowanego powyżej układu równań i przypisanie wartości liczbowych poszukiwanym wielkościom badanego obwodu. Następnie rozwiązanie to zostaje zdefiniowane jako wektor Ws.
4EKRAN_179

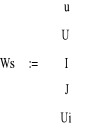
W celu sprawdzenia czy obwód został prawidłowo rozwiązany formułujemy równanie przy użyciu II prawa Kirchhoffa:
![]()
![]()
4EKRAN_180
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Układ równań opisujących obwód z elementami nieliniowymi:
![]()
![]()
![]()

Tym razem dla rozwiązania z funkcjami interpolowanymi procedurą linterp przyjęto
nazwę Wl.

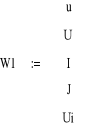
Komentarz-EKRAN_180
Ponownie rozwiązano układ równań z interpolacjami liniowymi.
Równania z II prawa Kirchhoffa przyjmują wartość zero, co potwierdza poprawność rozwiązania (w standardowym ustawieniu Mathcad dla wyników ![]()
wyświetla jako zero).
![]()
![]()
4EKRAN_181
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Układ równań opisujących obwód z elementami nieliniowymi.
![]()
![]()
![]()


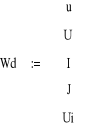
Komentarz-EKRAN_181
Sprawdzenie II prawa Kirchhoffa:
![]()
![]()
W celu porównania, układ równań opisujący dany obwód rozwiązano po raz trzeci tym razem z funkcjami analitycznymi (w praktyce nieznanymi).
4EKRAN_182
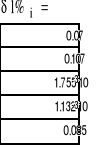
Porównanie otrzymanych wyników
Wartość Poszukiwana |
interpolacja wielomianami sześciennymi |
interpolacja liniowa |
funkcja oryginalna |
![]()
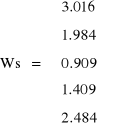
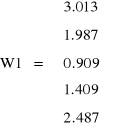
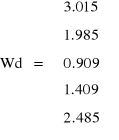
![]()
![]()
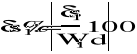
![]()
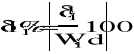
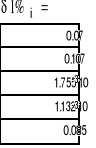
Komentarz-EKRAN_182
Wartości błędów określonych względem rozwiązania uzyskanego z użyciem analitycznych funkcji nieliniowych, potwierdza skuteczność rozwiązywania obwodów z elementami, których charakterystyki są interpolowane. W badanym przypadku błąd z użyciem interpolacji wielomianowej był mniejszy aniżeli dla interpolacji liniowej.
4EKRAN_183
Zadanie
Charakterystyka elementu nieliniowego RN określona jest zależnością: ![]()
Jakie należy przyłożyć napięcie zasilania UZ, aby rezystancja statyczna widziana z zacisków a-b była równa rezystancji statycznej elementu nieliniowego?
Dane:
R=10 Ω
α =1 A-1
Komentarz-EKRAN_183
Wskazówka1:
Zakładając, że znamy rezystancje statyczną elementu nieliniowego RN określamy rezystancję widzianą z zacisków a,b. Stąd wykorzystując metodę zwijania i rozwijania obwodu można ułożyć poniższy układ równań, z którego wyliczamy rezystancje nieliniową.
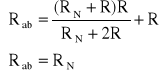
Rozwiązanie powyższego układu równań określi rezystancję statyczną RN. (Pamiętaj o odrzuceniu ujemnego rozwiązania).
4EKRAN_184
W celu wyznaczenia punktu pracy należy rozwiązać układ równań:
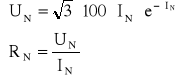
Odpowiedź:Aby uzyskać rezystancje statyczną elementu nieliniowego równą rezystancji statycznej widzianej z zacisków a-b należy przyłożyć napięcie ![]()
. Rezystancja RN w punkcie pracy wynosi : ![]()
4EKRAN_184
Podsumowanie:
Zasadnicze wnioski wynikające z lekcji 4 to:
Rezystancja a stąd rezystywność przewodników rośnie wraz ze wzrostem temperatury. Oznacza to, że elementy przewodzące pracujące w dużym przedziale temperatur należy traktować jak elementy nieliniowe.
Obwód, w którym występuje nawet jeden element nieliniowy nazywamy obwodem nieliniowym. Podstawowa metoda rozwiązania takiego obwodu polega na wycięciu elementu nieliniowego i zwinięcia pozostałej części liniowej do generatora Thevenina. Otrzymany w ten sposób obwód jednooczkowy można rozwiązać metodą przecięcia się charakterystyk.
Zasada superpozycji nie znajduje zastosowania w obwodach nieliniowych.
64
I
U
I
U
U
I
U
I
Up
Ip
U
I
αd
αs
U
I2
I
I1
U
I
I1
I2
U
I
I
U3=U1+U2
I
U1
I
U2
3
2
1
U3
U2
U1
I
U
I
1
2
3
R
E
U
UN
I
E
Ip
Ep
I
U
![]()
E2
I
UN=f(I)
UN
E2
R
E1
In
I''
I'
UN
E1
UN
IN
I1
a
b
R
R
RN
UN
I2
R
UZ
U1
U3
U2
UN
5
2
1
3
tab.1
[V]
[A]
IN
UN
0
0
6
3
4
1
U
E'
Rys. 4.4
R'
Rw
E
Rys. 4.3
Rys. 4.1
Rx
Rw
E
Rys. 4.2
Rys. 1
R'
E'
Rx
IN
0
1
0
2
3
4
6
R1
E1
R2
IN
RN
I2
Rys.4.6
R2
IN
RN
I2
Rys.4.7
R1
I1
Rys. 4.8
R
I
IN
RN
UN
UR
R
E
IN
RN
Rys.4.9
3
1
2
5
UN
IN
0
1
0
2
3
4
6
A
Wyszukiwarka
Podobne podstrony:
Elektrotechnika.02.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.11.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.05.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.04.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
Elektrotechnika.09.01, Studia, I semestr, Elektrotechnika, Elektra wykłady
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Biochemia - kolokwium[1], Studia, Semestr III, Biochemia, Wykłady
m014a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m002b, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
ZASADA ZACHOWANIA PĘDU, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zadania mechanika 11.06.2004, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m011p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Moment siły względem punktu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
WYKŁAD 01, STUDIA, III rok, INTERNA, Wykłady, wykłady 2006-7
TOCZNE TARCIE LUX PROTOKOL, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m009a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m013a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
więcej podobnych podstron