Wydział Mechaniczny Technologiczny Dzień: 02.1.2001

Kierunek: Zarządzanie i Inżynieria Produkcji

Grupa dziekańska: 8

Semestr: I

LABORATORIUM MECHANIKI OGÓLNEJ

ĆWICZENIE: D

TEMAT: Wyznaczanie położenia środka masy i masowego momentu bezwładności bryły sztywnej

Sekcja nr VIII:

• Wojciech Szuster

1. CEL ĆWICZENIA.

Celem ćwiczenia jest wyznaczanie środka masy i masowego momentu bezwładności korbowodu względem osi równoległej do osi otworów i przechodzącej przez środek masy korbowodu.

2. OPIS STANOWISKA POMIAROWEGO.

Stanowisko pomiarowe składa się z dwóch głównych elementów: poziomego elementu na który zawieszany jest korbowód i czujnika mierzącego liczbę i czas wahnięć korbowodu.

3. WSTĘP TEORETYCZNY.

Analiza lub synteza dynamiczna maszyny lub mechanizmu sprowadza się do rozwiązania jednego z dwóch następujących zadań:

• określenie ruchu mechanizmu i wyznaczenie oddziaływań dynamicznych w parach kinematycznych mechanizmu dla zadanego stanu obciążenia.

• Określenie stanu obciążenia przyłożonego do członów napędzających mechanizm realizujący określony ruch poszczególnych jego ogniw.

W obu tych zadaniach niezbędna jest znajomość masowych momentów bezwładności.

W szczególności gdy ciało wykonuje ruch obrotowy ,należy wyznaczyć moment bezwładności względem osi obrotu. Dynamiczne równanie ruchu obrotowego bryły sztywnej przyjmie wartość:

ϕ” - przyspieszenie kątowe bryły sztywnej w ruchu obrotowym wokół

nieruchomej osi OZ,

I_z - masowy moment bezwładności bryły względem osi obrotu z,

M_z - suma momentów względem osi Oz wszystkich sił zewnętrznych działających

na ciało.

Przez analogie do dynamicznego równania ruchu punktu materialnego, wynikającego z II zasady dynamiki Newtona ,można stwierdzić ,że masowy moment bezwładności ciała sztywnego jest miarą bezwładności tego ciała w jego ruchu obrotowym.

MASOWYM MOMENTEM BEZWŁADNOŚCI układu punktów materialnych względem punktu lub osi nazywamy sumę iloczynów mas poszczególnych punktów materialnych i kwadratów ich odległości od punktu lub osi.

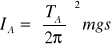
ŚRODKIEM MASY układu punktów materialnych nazywamy taki punkt C ,którego promień-wektor
poprowadzony z dowolnie obranego bieguna O określony jest za pomocą równania:

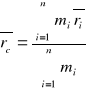
Jeżeli środek masy bryły składowej nie leży na osi OZ ,to korzystamy z twierdzenia Steinera, które mówi:

MOMENT BEZWŁADNOŚCI ciała materialnego względem osi równy jest sumie momentu bezwładności względem osi równoległej i przechodzącej przez środek masy oraz iloczynu masy ciała i kwadratu odległości między tymi osiami.

Metoda wahadła fizycznego pozwala wyznaczyć moment bezwładności wzg. osi przechodzącej przez środek masy ciała poprzez pomiar okresu wahań tego ciała, traktowanego jako wahadło fizyczne.

WAHADŁEM FIZYCZNYM nazywamy ciało materialne ,które może swobodnie obracać się względem poziomej osi.

4. OBLICZENIA

Aby wyznaczyć moment bezwładności
, należy najpierw określić odległość s środka ciężkości C od punktu zawieszenia A:

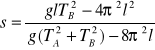
Po podstawieniu danych liczbowych otrzymujemy:

s = 0,205 [m]

Moment bezwładności korbowodu względem osi przechodzącej przez środek ciężkości:

I_C = I_A - ms² = 0,036[kgm²]

Moment bezwładności w punkcie A:

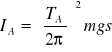
= 0.16[
]

Moment bezwładności w punkcie B:

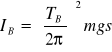
= 0.14[
]

5. WNIOSKI:

Na podstawie twierdzenia Steinera moment bezwładności korbowodu względem osi przechodzącej przez środek ciężkości wynosi:

I_C = 0,036 [kgm²]

natomiast masowy moment bezwładności względem osi przechodzącej przez punkt A wynosi:

I_A = 0,16 [kgm²]

oraz względem punktu B:

I_B = 0,14 [kgm²]

Czas wahnięć korbowodu zawieszonego w punkcie A jest większy od czasu wahnięć w punkcie B.

---