ZASADA ZACHOWANIA PĘDU
![]()
Pęd ciała p jest wektorem równym iloczynowi masy m ciała i jego prędkości v
Zasada: "Jeśli wypadkowa sił zewnętrznych (pochodzących od innych ciał)działających na układ ciał jest równa zero, wówczas całkowity pęd układu pozostaje stały mimo działania sił zewnętrznych"
Jeżeli w układzie zamkniętym zachodzi zmiana prędkości jednego z ciał układu, to prędkości innych ciał musi się również zmienić tak, aby suma pędów pozostała niezmieniona.
Wynika ona z 2 zasad dynamiki, ale jest również ważne to:
-w niektórych przypadkach posługiwanie się prawem Newtona może być utrudnione,
-jej ogólność wykracza poza normy mechaniki Newtona
ZASADA ZACHOWANIA KRĘTU
Kręt, inaczej moment pędu jest wektorem prostopadłym do płaszczyzny, w której leży promień wodzący i pęd i jest skierowany tak jak prędkość kątowa ω
Zasada: „Moment pędu ciała, na które nie działają momenty sił, lub momenty te się wzajemnie równoważą jest stały" Jeżeli w układzie zamkniętym jedno z ciał zostanie wprawione w ruch obrotowy pod działaniem sił zewnętrznych to i inne ciała zostaną również wprawione w ruch -wy tak aby całkowity moment pędu pozostał bez zmiany.
ENERGIA KINETYCZNA W JEDNOSTAJNYM RUCHU BRYŁY SZTYWNEJ.
Energia kinetyczna ciała obracającego się dookoła osi równa się sumie energii kinetycznych jego cząstek. Zatem otrzymaliśmy ostatecznie wzór na energie kinetyczną ciała sztywnego obracającego się dookoła osi:
Zatem otrzymaliśmy ostatecznie wzór na energię kinetyczną ciała sztywnego obracającego się dookoła osi:
Bryła sztywna-ciało którego poszczególne punkty
pozostają w niezmiennej wzajemnej odległości od siebie. Może ona wykonywać 2 rodzaje ruchów:
-postępowy—punkty ciała poruszają się po torach równoległych,
-obrotowy---punkty ciała zakreślają okrąg współśrodkowy, a ich środki leżą na linii prostej nie biorącej udziału w ruchu zwanej obrotu.
MOMENT PĘDU W JEDNOSTAJNYM RUCHU OBROTOWYM BRYŁY SZTYWNEJ
Bryła sztywna -(wcześniej).Kręt-moment pędu.
Krętem układu punktów lub ciała sztywnego względem osi obrotu będzie suma algebraiczna krętów poszczególnych punktów względem tej osi.
![]()
![]()
Dla ciała sztywnego możemy uzyskać prostsze wyrażenie na kręt ,wprowadzając wielkość zwaną prędkością kątową, gdzie ![]()
i otrzymujemy:
![]()
; ![]()
Teraz zastępujemy fragment ![]()
poprzez moment bezwładności, otrzymujemy:
K = J ω (iloczyn momentu bezwładności i prędkości kątowej ciała).
MOMENT SIŁY W JEDNOSTAJNYM ZMIENNYM RUCHU OBROTOWYM BRYŁY SZTYWNEJ
Bryła sztywna(wcześniej)
Ruch obrotowy zmienny-ruch taki występuje gdy siła działająca na ciało obracające się wywoła zmianę prędkości kątowej, czyli wystąpi przyspieszenie kątowe. Moment siły względem osi obrotu różny od zera.
Zasada: moment siły względem obranej osi obrotu jest równy iloczynowi momentu bezwładności względem tej osi i przyspieszenia kątowego.
Przypuśćmy że przykładamy siłę o momencie τ do jednego z punktów ciała sztywnego.
Ponieważ wszystkie punkty tego ciała pozostają w ustalonych wzajemnych odległościach, to możemy powiedzieć że przyłożona siła działa na ciało sztywne.
![]()
![]()
![]()
![]()
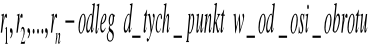
![]()
![]()
![]()
![]()

![]()
![]()
Wyszukiwarka
Podobne podstrony:
Ilustracja zasady zachowania pędu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zasada pędu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zasada zachowania pędu, studia, fizyka
zasada zachowania pedu, studia, fizyka
!!!zachowanie pedu, Studia, Mibm, semestr II, Mechanika, LABORY!!
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m014a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m002b, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zadania mechanika 11.06.2004, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m011p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Moment siły względem punktu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TOCZNE TARCIE LUX PROTOKOL, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m009a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m013a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m006a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
macierzowa - ktatownica, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TOCZNE TARCIE LUX, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
więcej podobnych podstron