Politechnika Śląska
Wydział: MT
Kierunek: MiBM
Grupa 5
Semestr 1
Wyznaczanie przyśpieszenia ziemskiego
za pomocą wahadła rewersyjnego
Sekcja: 1
Brejza Damian
Dudek Mariusz
Sztucki Krzysztof
Wprowadzenie:
Celem ćwiczenia jest wyznaczenie przyśpieszenia ziemskiego. Po zaniedbaniu ruchu wirowego Ziemi wartość tego przyśpieszenia przy powierzchni Ziemi wyniosłaby:
![]()
gdzie:
G - stała grawitacji,
M![]()
- masa Ziemi,
R![]()
- promień naszego globu.
Na ciało znajdujące się na wirującej planecie działa siłą odśrodkowa bezwładności lub siła Coriolisa (którą można zaniedbać w porównaniu z tą pierwszą siłą). Składowa normalnej odśrodkowej siły bezwładności w miejscu o szerokości geograficznej ϕ wynosi:
![]()
gdzie:
T - okres obrotu Ziemi wokół własnej osi.
Powyższa zależność przyjęta jest przy kulistości ziemi.
Zwykle do obliczania zależności przyśpieszenia ziemskiego od szerokości geograficznej stosuje się empiryczny wzór Hayforda:
![]()
Przyspieszenie ziemskie g maleje ze wzrostem wysokości i dla danego miejsca na Ziemi powinno być wyznaczane metodami doświadczalnymi.
Najprostszą metodą pomiaru przyśpieszenia ziemskiego wydaje się sposób pomiaru czasu spadku swobodnego. Jednak nie daje on zadowalających wyników z powodu konieczności uwzględniania wieli poprawek (np. na opór powietrza). Do precyzyjnych pomiarów g stosuje się tzw. grawimetry. Zasada działania tych przyrządów sprowadza się do porównania siły ciężkości z siłą sprężystości. W użyciu są grawimetry gazowe, kwarcowe i metalowe. Dokładność takiej aparatury sięga wartości 1 gal![]()
.
My postaramy się wyznaczyć przyśpieszenie ziemskie za pomocą wahadła rewersyjnego.
Wahadło rewersyjne - zasada jego działania opiera się na własności zwanej dwuosiowością wahadła fizycznego. Przyjmujemy, że istnieją dwie różne osie O![]()
i O![]()
, dla których okresy drgań wahadła fizycznego są równe:
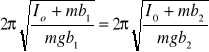
gdzie:
I![]()
- moment bezwładności bryły względem osi przechodzącej przez jej środek masy.
Równość okresów zrealizujemy wtedy, gdy:
(b![]()
- b![]()
)(I![]()
- mb![]()
b![]()
) = 0
skąd otrzymujemy dwa warunki:
b
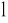
=b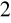
,I
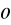
/m = b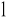
b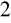
,
Nas interesuje sytuacja druga, zgodnie z którą otrzymamy:
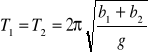
Oznaczając odległości między osiami ![]()
otrzymujemy ostatecznie:
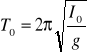
Warunek ten jest tylko jednym z możliwych. Równość okresów zachodzi dla wszystkich osi będących tworzącymi walców o promieniach b![]()
i b![]()
oraz osi przechodzących przez środek ciężkości.
Metoda pomiaru:
Pomiar przy pomocy asymetrycznego wahadła rewersyjnego złożonego z pręta, dwóch pierścieni z nacięciami i dwóch ciężarków:
A B
O![]()
O![]()
x
I![]()
Nacięcia na pierścieniach umożliwiają zawieszenie wahadła na ostrzu pryzmatycznym przymocowanym do ściany. Jeden z pierścieni znajduje się na końcu pręta, drugi w odległości ponad 1m. Ciężarek B znajduje się w położeniu dającym odpowiednią asymetryczność wahadła (położenie to dobrano metodą prób i nie powinno być zmieniane podczas ćwiczenia). Drugi z ciężarków może być przesuwany wzdłuż osi wahadła. Zmiana położenia ciężarka powoduje zmianę usytuowania środka ciężkości oraz zmianę momentu bezwładności I![]()
. Pociąga to za sobą zmianę okresu drgań. Funkcja zależności okresu drgań od odległości x ruchomego ciężarka od krańcowego zawieszenia jest funkcją uwikłaną drugiego stopnia o postaci stosunkowo skomplikowanej. Dla drugiego zawieszenia sytuacja jest analogiczna. W zależności od położenia drugiego ciężarka możemy mieć dwa punkty przecięcia parabol na wykresie (z których wybieramy tylko jeden), jeden punkt odpowiadający nieciekawej sytuacji ![]()
oraz najgorszy przypadek, kiedy parabole się nie przecinają.
Zasada wyznaczenia przyśpieszenia ziemskiego sprowadza się do znalezienia takiego położenia ruchomego ciężarka, które odpowiada jednakowym okresom drgań dla obydwu zawieszeń wahadła rewersyjnego. Procedura dochodzenia do stanu odwracalności wahadła jest realizowana w trzech etapach:
zmiana odległości x co 10 cm i pomiar okresu drgań dla obu zawieszeń,
sporządzenia wykresu i przybliżone oszacowanie położenia odwracalnego na podstawie przecięcia parabol,
precyzyjne wyznaczanie okresu drgań, który odpowiada warunkowi odwracalności
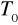
.
Przyśpieszenie ziemskie wyznaczamy wg wzoru:
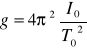
gdzie I![]()
jest odległością między zawieszeniami (pryzmatami).
3.Przebieg ćwiczenia:
Mierzymy odległość między ostrzami wahadła.
Zawieszamy wahadło na ostrzu zamocowanym na końcu pręta. Wprawimy wahadło w ruch i mierzymy czas 20 okresów.
Zawieszamy wahadło na drugim ostrzu i ponownie mierzymy czas 20 okresów.
Wykonujemy czynności opisane powyżej dla położeń ciężarka, zmienianych co 10 cm.
Rysujemy wykres zależności okresu wahań od odległości ciężarka od ostrza A (dla obydwu sposobów zawieszenia). Z wykresu określamy położenia ciężarka, przy którym okresy drgań są jednakowe dla obydwu zawieszeń.
Ciężarek ustawiamy w położeniu określonym z wykresu i mierzymy czas 100 okresów dla obu zawieszeń wahadła. Takie pomiary należy powtarzać (zmieniając położenie ciężarka np. co 1 cm), aż do spełnienia warunku odwracalności wahadła.
Obliczamy przyśpieszenie ziemski.
Przeprowadzamy rachunek błędów.
TABELA POMIAROWA
Położenie X [cm] |
Ostrze A |
Ostrze B |
||
|
Czas t [s] |
Okres T [s] |
Czas t [s] |
Okres T[s] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2
Wyszukiwarka
Podobne podstrony:
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m014a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m002b, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
ZASADA ZACHOWANIA PĘDU, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zadania mechanika 11.06.2004, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m011p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Moment siły względem punktu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TOCZNE TARCIE LUX PROTOKOL, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m009a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m013a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m006a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
macierzowa - ktatownica, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TOCZNE TARCIE LUX, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m013p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m008p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
ściąga mechana, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Ilustracja zasady zachowania pędu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
więcej podobnych podstron