POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI	SPRAWOZDANIE Z ĆWICZENIA NR 12 TEMAT : Wyznaczanie modułu sztywności metodą dynamiczną.
ANNA SIKORA WYDZ. : IZ ROK : II	DATA : OCENA :

0. Wstęp.

Celem przeprowadzonego doświadczenia było :

- wyznaczenie występującego w prawie Hooke'a modułu sztywności przez pomiar okresu

sprężystych drgań obrotowych. Moduł sztywności jest stałą charakteryzującą odporność

ciała na odkształcenia, a dokładniej na skręcanie.

1. Opis zjawiska fizycznego.

Ciało nazywamy sprężystym, jeżeli odkształcenia, wywołane działającymi na nie siłami, znikają zupełnie po usunięciu tych sił.

Istotę sprężystości można zrozumieć rozważając chociażby w przybliżeniu strukturę wewnętrzną ciała stałego. Każde ciało jest zbudowane z atomów lub cząsteczek, między którymi działają siły nazywane międzycząsteczkowymi. Siły te są w ciałach stałych na skutek małych odległości międzycząsteczkowych na tyle duże, że cząsteczki są dzięki temu uporządkowane, tworząc regularną strukturę przestrzenną, nazwaną siecią krystaliczną. Każda cząsteczka, nazywana w taki przypadku również węzłem sieciowym ma swoje położenie równowagi, wokół którego wykonuje niewielkie, chaotyczne, zależne od temperatury ciała drgania. Powstanie stanu równowagi trwałej wynika z faktu, że między każdymi dwiema cząsteczkami występują dwojakiego rodzaju siły : przyciągania oraz odpychania, o niejednakowej zależności od odległości międzycząsteczkowej, przy czym siły odpychania rosną zawsze znacznie bardziej wraz ze zbliżaniem się cząsteczek niż siły przyciągania.

Prawo Hooke'a formułuje zależność między naprężeniem a odkształceniem:

Jeżeli naprężenia w ciele są dostatecznie małe, to wywołane przez nie odkształcenia względne są do nich wprost proporcjonalne.

,

gdzie a - kąt ścinania,

G - moment sztywności ,

τ - naprężenie styczne.

2. Zestaw przyrządów.

Wahadło torsyjne,

Miara milimetrowa,

Śruba mikrometryczna,

Suwmiarka,

Waga laboratoryjna,

Elektroniczny licznik okresu i czasu.

Rys.1

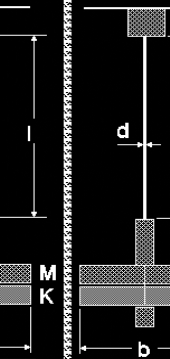
3. Wzór końcowy.

Kiedy moment sił sprężystych przestaje być równoważony przez moment zewnętrzny, powoduje to drgania harmoniczne obrotowe, których moment kierujący zależy od modułu sztywności :

D =

Badanie modułu sztywności w tym doświadczeniu polega na pomiarze okresu drgań układu pomiarowego ( Rys.1 ).

T = 2p*

Ponieważ nie znamy momentu bezwładności tego układu, pomiar odbywa się dwukrotnie: raz bez tarczy dodatkowej K, a następnie wraz z tarczą dodatkową o okresie drgań

T₁ = 2p*


,

Otrzymujemy zatem :

D =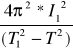

Moment bezwładności tarczy dodatkowej łatwo jest wyliczyć ze wzoru:

.

m - masa tarczy dodatkowej

l - długość drutu

d - średnica drutu

b - średnica tarczy dodatkowej

n - ilosc drgań = 50

t₁ - czas n drgań tarczy dodatkowej

t - czas n drgań tarczy

Dla zwiększenia dokładności pomiaru okresu mierzy się nie okres jednego drgania, lecz czas n ( w tym wypadku n=50 ) drgań. W rezultacie moduł sztywności można wyliczyć ze wzoru:

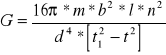
[ N/m² ]

4. Tabelki pomiarów.

Długość drutu :

l1 [mm]	l2 [mm]	l = l1 -l2 [mm]
45.0	632.0	627.5

Średnica drutu d :

d1 [mm]	d2 [mm]	d3 [mm]	d = 1/3 ( d1 + d2 + d3 ) [mm]
0.595	0.592	0.596	0.594(3)

Średnica tarczy dodatkowej b :

b1 [mm]	b2 [mm]	b3 [mm]	b = 1/3 ( b1 + b2 + b3 ) [mm]
139.52	140.0	140.0	139.84

Masa tarczy dodatkowej m

:

m [g]

310.2

Czas t trwania n drgań :

t1 [s]	t2 [s]	t3 [s]	t = 1/3 ( t1 + t2 + t3 ) [s]
392.459	391.117	390.989	391.521(6)

Czas t₁ trwania n drgań :

t11 [s]	t12 [s]	t13 [s]	t1 = 1/3 ( t11 + t12 + t13 ) [s]
456.668	456.406	456.317	456.463(6)

5. Przykładowe obliczenia.

Podstawiając do wzoru końcowego obliczamy wartość modułu sztywności :

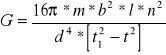
Zamieniając odpowiednio jednostki otrzymujemy :

G =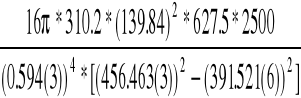
= 69578284430.8 [ N/m² ]

G = 69578.2844308 * 10⁶ Pa

6. Dyskusja błędów.

Do obliczenia błędu, z jakim wyznaczono moduł sztywności G, posłużę się metodą różniczki logarytmicznej. Oznaczając

a = t₁² - t²

oraz zakładając, że

Δt₁ = Δt

otrzymujemy :

Δa = 2t₁Δt₁ + 2tΔt = 2Δt( t₁ + t ).

Ponieważ na dokładność obliczeń wpływają pomiary : długości drutu, jego średnicy, średnicy tarczy dodatkowej, czasu trwania n drgań, błąd obliczymy ze wzoru :

=
+ 2
+
+ 4
+ 2
, czyli :

=
+ 2
+
+ 4
+ 2

Za Δm, Δb, Δl, Δd, Δt podstawiamy średnie błędy bezwzględne pomiarów, czyli :

Δk =

, gdzie Δk_i = k - k_i ,

zaś k oznacza średnią arytmetyczną mierzonej wielkości.

Obliczamy teraz po kolei błąd pomiaru każdej wielkości ( pomiary pobierane są z tabelki ) :

a.) masa,

m = 310.2 g Δm = 0.1 g

= 0.000322

b.) średnica tarczy dodatkowej,

b = 139.84 mm

b₁ = 139.52 mm Δb₁ = 0.32 mm

b₂ = 140.0 mm Δb₂ = 0.16 mm

b₃ = 140.0 mm Δb₃ = 0.16mm

Δb = 1/3 ( 0.32 + 0.16 + 0.16 ) = 1/3 ( 0.64) = 0.21(3)

= 0.001525

c.) długość drutu,

W tabelce została uwzględniona średnia wartość pomiaru górnego - początku druta. Faktycznie wynosiły odpowiednio : l₁₁ = 0.4 mm, l₁₂ = 0.5mm. Przy pomiarze końca druta wartości odczytane były takie same. Zatem błąd pomiaru wyniósł Δl = 0.05.

= 0.000079

d.) średnica drutu,

Δd₁ = 0.000667 mm

Δd₂ = 0.002334 mm

Δd₃ = 0.001667 mm

Δd = 1/3 * 0.004668 = 0.001556

= 0.002618

e.) czas trwania n drgań,

zał. Δt₁ = Δt ( obliczam dla t = 391.521(6) )

Δt₀₁ = 0.937334 s

Δt₀₂ = 0.404667 s

Δt₀₃ = 0.532667 s

Δt = 1/3 * 1.874668 = 0.624889

t₁ - t = 64.942 s

= 0.009622

Mając teraz wszystkie dane obliczamy :

= 0.000322 + 2*0.001525 + 0.000079 + 4*0.002618 + 2*0.009622 = 0.033167

Błąd bezwzględny wynosi :

ε = 3.31 *

Jak widać największy błąd do końcowego wyniku (pomimo dokładnego przyrządu pomiarowego) wniósł pomiar średnicy badanego drutu oraz czasu trwania n drgań. Co do średnicy, to spowodowała to stosunkowo mała wartość wielkości mierzonej (0.594(3) mm) oraz to, że we wzorze końcowym wielkość ta występowała aż w czwartej potędze.

7. Uwagi i wnioski.

Największy wpływ na błąd wyznaczenia G miał błąd pomiaru średnicy drutu - wynosił 1.04 % oraz błąd pomiaru czasu trwania n = 50 drgań - 1.92 %. Przy obliczaniu błędów nalęży też wspomnieć o niedoskonałości przyrządów, choć tym razem były one dość dokładne.

Wyprowadzenie wzoru na moment bezwładności walca - gdyż w naszym ćwiczeniu tarcza dodatkowa miała taki kształt.

Wychodząc ze wzoru na energię kinetyczną w ruchu obrotowym

K_obr =
+
+ ...

oraz wiedząc, że v = ωr, otrzymujemy wzór :

K_obr = ω²/2 ( r₁²Δm₁ + r₂²Δm₂ + ...).

Wielkość w nawiasach nie zależy od prędkości ruchu, lecz charakteryzuje opór bezwładny ciaław ruchu obrotowym : im większa jest ta wielkość, tym więcej energii trzeba zużyć dla nadania ciału danej prędkości kątowej. Wielkość ta nazywa się momentem bezwładności ciała :

I = r₁²Δm₁ + r₂²Δm₂ + ...

zaś wyrażenie r²Δm - momentem bezwładności punktu. Moment bezwładności I można przedstawić także w innej formie :

I = ∫ r² dm

Dla uproszczenia obliczmy moment bezwładności płaskiego dysku o promieniu r względem osi prostopadłej do płaszczyzny dysku i przechodzącej przez jego środek. Bierzemy zatem pod uwagę przekrój walca ( płaszczyznę ), gdyż każdy „przekrój” będzie się charakteryzował taką sama bezwładnością - odpowiednie punkty równo oddalone od osi obrotu. Masa wynosi

m = ρV = ρ*πr² , gdzie

ρ - gęstość materiału, z którego zrobiony jest dysk,

V - w tym przypadku pole płaskiego dysku (koła), zaś ogólniej bierze się objętość bryły ( we wzorze znajdowałyby się wtedy całki potrójne ).

Rys.1a

x dx

r

Masa pierścienia elementarnego o promieniu x wynosić będzie dm = ρ*2πxdx. Moment bezwładności tego pierścienia dI₁ = dm*x² . Moment bezwładności całego dysku wyrażać się będzie wzorem :

I₁ =
=
=
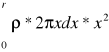
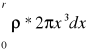
= 2πρ*( 1/4 x⁴ )^r₀ = 1/2πρ*r⁴

Podstawiając wzór na masę otrzymujemy :

I₁ = 1/2 mr²

---