Intensywność uszkodzeń − λ(t) − jest to warunkowe prawdopodobieństwo tego, że obiekt uszkodzi się

w przedziale czasu (t, t + Δt] pod warunkiem, że do chwili t pracował poprawnie, podzielone przez Δt.

Gęstość prawdopodobieństwa uszkodzenia − f(t) − określa prawdopodobieństwo, z jakim uszkodzi się obiekt w danej chwili t.

Miary niezawodności obiektu:

− oczekiwany czas zdatności (średni czas pracy do uszkodzenia),

− intensywność uszkodzeń (ilość uszkodzeń w jednostce czasu),

− prawdopodobieństwo, że obiekt się nie uszkodzi do pewnej chwili t,

− prawdopodobieństwo, że obiekt jest zdolny do działania w pewnej chwili t.

Ilościowe miary niezawodności obiektu nienaprawialnego:

− funkcja niezawodności - R(t),

− funkcja zawodności - F(t),

− gęstość prawdopodobieństwa uszkodzenia - f(t)

− intensywność uszkodzeń - λ(t),

− oczekiwany czas zdatności - ET,

− pozostały oczekiwany czas zdatności - E(t).

Ilościowe miary niezawodności obiektu naprawialnego:

− funkcja gotowości,

− współczynnik gotowości,

− intensywność uszkodzeń,

− intensywność odnowy,

− proces odnowy,

− funkcja odnowy.

Oczekiwany czas zdatności − ET − średni czas pracy obiektu do chwili uszkodzenia,

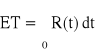
− czyli pole pod krzywą funkcjia niezawodności.

Pozostały oczekiwany czas zdatności − E(t) − warunkowa wartość oczekiwana zmiennej losowej T − t (pozostały czas zdatności), pod warunkiem, że do chwili t obiekt był zdatny −

.

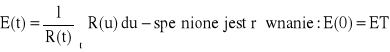
Proces odnowy − N(t) − jest to punktowy proces losowy przedstawiający ilość uszkodzeń, która wystąpiła do chwili t.

Funkcja odnowy − H(t) − jest wartością oczekiwaną procesu odnowy, tj. przeciętną liczbą uszkodzeń danego obiektu, które wystąpią do danej chwili t.

Nadmiar strukturalny − system taki składa się z elementów podstawowych realizujących jego funkcje oraz z elementów rezerwowych włączających się do pracy w razie uszkodzenia się elementów podstawowych.

Nadmiar funkcjonalny − niektóre elementy takiego systemu są wielofunkcyjne. Element wykonuje ściśle określoną funkcję, natomiast w określonych sytuacjach może pełnić dodatkową funkcje elementu uszkodzonego.

Nadmiar czasowy − do współdziałania takiego systemu są wprowadzone określone normatywy czasowe, w których zakresie współdziałanie może być realizowane.

Nadmiar parametryczny − system taki ma duże wymagania zarówno co do niezawodności, jak i bezpieczeństwa. Jest to np. przyjmowanie współczynników bezpieczeństwa w budowie maszyn.

Rezerwa obciążona − element podstawowy i elementy rezerwowe poddawane są tym samym obciążeniom wynikającym z warunków pracy. Własności elementów zmieniają się w taki sam sposób, czyli nie możemy określić, który z elementów jest rezerwowy i który wcześniej ulegnie uszkodzeniu. Czas zdatności urządzenia jest równy: T_u = max(T₁,T₂,... ,T_n).

Rezerwa nieobciążona − element podstawowy pracuje, rezerwowe elementy oczekują na uszkodzenie elementu podstawowego. Czas zdatności urządzenia jest równy sumie czasów zdatności poszczególnych elementów. Spełnione jest równanie: ET_u = ET_o + ET₁ + ET₂ + ... + ET_n.

Rezerwa częściowo obciążona − elementy rezerwowe poddawane są pewnemu obciążeniu w czasie oczekiwania na włączenie (ich własności niezawodnościowe zmieniają się w czasie). Czas zdatności urządzenia jest równy: T_u = T_o + T₁/T_o,T₁ + T₂/ T_o,T₁,T₂ + ...

Funkcja niezawodności − R(t) − prawdopodobieństwo, że obiekt może spełniać wymaganą funkcję w danych warunkach w ustalonym czasie. R(t) = P(T ≥ t), T − zmienna losowa czasu pracy obiektu do powstania uszkodzenia. Funkcja niezawodności może przyjmować wartości z przedziału <0,1> (ze względu na to, że jest to prawdopodobieństwo). Funkcja niezawodności jest funkcją malejącą, ponieważ niezawodność obiektu maleje z czasem.

Funkcja zawodności − F(t) − prawdopodobieństwo, że obiekt nie będzie spełniać wymaganej funkcji w danych warunkach w ustalonym czasie. F(t) = P(T ≤ t), T − zmienna losowa czasu pracy obiektu do powstania uszkodzenia. Funkcja zawodności może przyjmować wartości z przedziału <0,1> (ze względu na to, że jest to prawdopodobieństwo). Funkcja zawodności jest funkcją rosnącą, ponieważ zawodność obiektu rośnie z czasem.

Funkcja gotowości − miara gotowości obiektu odnawialnego − jest to prawdopodobieństwo tego, że w danej chwili czasu obiekt będzie zdatny.

Współczynnik gotowości − jest to wartość graniczna funkcji gotowości przy czasie dążącym do nieskończoności.

Ścieżką zdatności − każdy taki zbiór elementów systemu, których równoczesne funkcjonowanie zapewnia funkcjonowanie systemu jako całości.

Minimalna ścieżka zdatności − jest to taka ścieżka zdatności, z której nie można wyłączyć żadnego elementu bez utraty statusu ścieżki. Oznacza to, że wyłączenie co najmniej jednego elementu ścieżki spowoduje uszkodzenie urządzenia.

Przekrojem niezdatności − każdy taki zbiór elementów systemu, których równoczesne uszkodzenie powoduje uszkodzenie systemu jako całości.

Minimalny przekrój niezdatności (cięcie) − to taki przekrój zdatności, z którego nie można wyłączyć żadnego elementu bez utraty statusu przekroju. Oznacza to, że wyłączenie co najmniej jednego elementu przekroju spowoduje, że uszkodzenie urządzenia nie ma miejsca.

I. PODSTAWOWE CHARAKTERYSTYKI NIEZAWODNOŚCI OBIEKTÓW

NIENAPRAWIALNYCH

• funkcja niezawodności R(t)

Prawdopodobieństwo tego, że obiekt nie ulegnie uszkodzeniu w przedziale czasu (0, t], co

jest równoważne prawdopodobieństwu tego, że zmienna losowa T nazywana czasem

zdatności nie przyjmie wartości z tego przedziału.

• funkcja zawodności F(t)

Prawdopodobieństwo tego, że obiekt ulegnie uszkodzeniu w przedziale czasu (0, t], co jest

równoważne prawdopodobieństwu tego, że zmienna losowa T nazywana czasem zdatności

przyjmie wartość z tego przedziału.

• gęstość prawdopodobieństwa uszkodzeń f(t)

Jest to granica do jakiej dąży iloraz prawdopodobieństwa tego, że obiekt uszkodzi się w

przedziale czasu (t, t+∆ t] i długości tego przedziału, gdy długość ta dąży do zera.

Z powyższego wzoru wynika, że prawdopodobieństwo tego, że obiekt uszkodzi się w małym

przedziale czasu (t, t+∆ t] jest równe iloczynowi f(t) ∆ t plus o( ∆ t).

• intensywność uszkodzeń λ(t)

Intensywność uszkodzeń nazywana bywa funkcją ryzyka. Jest to warunkowa gęstość

prawdopodobieństwa wystąpienia uszkodzenia w małym przedziale czasu (t, t+ ∆ t] pod

warunkiem, że na początku tego przedziału (w chwili t) obiekt znajdował się w stanie

zdatności.

Intensywność uszkodzeń może być zatem rozumiana jako względny spadek niezawodności w

czasie.

Z powyższego wzoru wynika, że warunkowe prawdopodobieństwo tego, że obiekt uszkodzi

się w małym przedziale czasu (t, t+∆ t] pod warunkiem, że do chwili t pracował poprawnie

jest równe iloczynowi λ(t) ∆ t plus o( ∆ t).

• oczekiwany czas zdatności urządzenia ET

Jest to charakterystyka liczbowa będąca wartością oczekiwaną czasu zdatności obiektu.

Nazywany jest również przeciętnym czasem do uszkodzenia, przeciętnym czasem poprawnej

pracy.

• oczekiwany pozostały czas zdatności E(t)

Nieco rzadziej wykorzystywaną charakterystyką funkcyjną czasu zdatności jest

charakterystyka określona poniższym wzorem:

Jest to warunkowa wartość oczekiwana zmiennej losowej T-t nazywanej pozostałym czasem

zdatności, pod warunkiem, że w chwili t obiekt jest zdatny.

II. MODELOWANIE CZASU ZDATNOŚCI OBIEKTU PRZY UŻYCIU ROZKŁADÓW

TEORETYCZNYCH

Rozkład jednostajny czasu zdatności opisany

na przedziale od 0 do k

Jest to przykład rozkładu ograniczonego, gdyż urządzenie nie będzie działać dłużej niż k

jednostek czasu.

• Gęstość prawdopodobieństwa

• Funkcja zawodności

• Funkcja niezawodności

• Intensywność uszkodzeń

• Oczekiwany czas zdatności

• Oczekiwany czas zdatności

• Oczekiwany pozostały czas zdatności

Rozkład wykładniczy czasu zdatności

• Funkcja niezawodności • Gęstość prawdopodobieństwa uszkodzeń • Intensywność uszkodzeń • Oczekiwany czas zdatności • Oczekiwany pozostały czas zdatności

III. OBIEKTY ZŁOŻONE

Na ogół obiekt może być traktowany jako system złożony z bloków funkcjonalnych, między którymi zachodzą relacje umożliwiające systemowi realizację wymaganych funkcji. Termin „blok funkcjonalny” może oznaczać zarówno pojedynczy element jak i duży podsystem. Zależy to od rodzaju systemu i sposobu podejścia do zagadnienia. Relacje niezawodnościowe między systemem jako całością i jego elementami mogą być opisane w różny sposób. Wszystkie sposoby ich przedstawienia służą zilustrowaniu „sposobu uszkodzenia” systemu. Analiza struktury niezawodnościowej systemu umożliwia podjęcie racjonalnych działań mających na celu zwiększenie jego niezawodności.

Struktura niezawodnościowa systemu jest to taka funkcja, która każdej kombinacji stanów

elementów systemu w sposób jednoznaczny przyporządkowuje stan tego systemu jako

całości.

Jeżeli stan elementu i, i = 1, 2, ..., n jest przedstawiony jako zmienna dwuwartościowa (binarna) xi przyjmująca wartość 1, gdy element jest zdatny albo wartość 0, gdy jest on niezdatny, a przez x oznaczony zostanie wektor stanów (x1, x2, ..., xn) to stan systemu można przedstawić jako również dwuwartościową funkcję opisaną na tym wektorze.

Jeżeli wiadomo z jakich elementów składa się obiekt oraz jaki jest stan poszczególnych elementów, to można powiedzieć jaki jest stan systemu tylko wówczas, gdy znana jest jego struktura niezawodnościowa. Identyfikacja struktury niezawodnościowej systemu wymaga określenia funkcji, jaką ma ten system do spełnienia oraz kryteriów uznania go za niezdatny.

Strukturę niezawodnościową systemu można przedstawić np. w postaci:

- grafu - nazywanego schematem blokowym niezawodności;

- tablicy,

- funkcji logicznej,

- funkcji analitycznej,

- ścieżek zdatności i przekrojów niezdatności,

- drzewa uszkodzeń.

Na schemacie blokowym niezawodności każdy z elementów przedstawiony jest w postaci bloku z jednym wejściem a i jednym wyjściem b. Jeżeli jest przejście między punktami a i b obiekt uważa się za zdatny - zdolny do zrealizowania określonej funkcji.

Jeżeli na schemacie zbudowanym z bloków przedstawiających poszczególne elementy jest

„możliwość przejścia z jednego końca do drugiego”, to oznacza to, że obiekt jest zdatny.

Wszystkie dalsze rozważania ograniczone zostaną do tzw. STRUKTUR KOHERENTNYCH

to znaczy spełniających następujące warunki:

• Jeżeli wszystkie elementy są zdatne - system jest zdatny;

• Jeżeli wszystkie elementy są niezdatne - system jest niezdatny;

• Uszkodzenie elementu nie powoduje podniesienia niezawodności systemu.

Nie będą rozpatrywane tego rodzaju sytuacje, w których jakiś mechanizm samodestrukcji „wbudowany” w urządzenie ulegnie uszkodzeniu i podniesie to niezawodność urządzenia.

Modelami występujących w rzeczywistości obiektów technicznych są na ogół systemy koherentne wśród, których wyróżnia się struktury:

• szeregowo-równoległe,

• progowe,

• mostkowe.

IV. PODSTAWOWE STRUKTURY NIEZAWODNOŚCIOWE

• Struktura szeregowa - jeżeli system jest zdatny wyłącznie wtedy, gdy zdatne są wszystkie jego elementy to jego struktura niezawodnościowa nazywana jest szeregową.

Prawdopodobieństwo tego, że cały system jest zdatny dane jest wzorem:

Gdy czasy zdatności jego poszczególnych elementów są niezależnymi zmiennymi losowymi

otrzymujemy:

Funkcja niezawodności takiego obiektu jest zatem iloczynem funkcji niezawodności

jego elementów:

Czas zdatności obiektu jest równy czasowi zdatności „najgorszego” elementu:

• Struktura równoległa - jeżeli system jest niezdatny wyłącznie wtedy, gdy niezdatne są wszystkie jego elementy to jego struktura niezawodnościowa nazywana jest równoległą.

Prawdopodobieństwo tego, że cały obiekt jest niezdatny wyraża się wzorem:

Gdy czasy zdatności poszczególnych elementów są niezależnymi zmiennymi losowymi:

Funkcja zawodności takiego obiektu jest zatem iloczynem funkcji zawodności jego

elementów:

Czas zdatności obiektu jest równy czasowi zdatności „najlepszego” elementu:

• Struktura progowa (nazywana strukturą k z n ) - jeżeli system jest zdatny wtedy, gdy zdatnych jest co najmniej k spośród n jego elementów to jego struktura niezawodnościowa nazywana jest progową.

Struktury szeregowa i równoległa można uważać za szczególne przypadki struktur

progowych odpowiednio n z n i 1 z n

• Struktury mieszane - system o mieszanej strukturze niezawodnościowej charakteryzuje się niezawodnością nie gorszą od systemu złożonego z tych samych elementów tworzących strukturę szeregową i nie lepszą od systemu złożonego z tych samych elementów, tworzących strukturę równoległą.

V. NADMIARY

Zwiększenie niezawodności i trwałości obiektu może być wynikiem zastosowania różnych form nadmiarowości. Ogólnie rzecz biorąc nadmiary te można podzielić na:

- strukturalne - wprowadzanie do struktury urządzenia elementów rezerwowych,

bez których urządzenie to może działać, a które służą tylko podnoszeniu jego niezawodności,

- funkcjonalne - inne elementy urządzenia są w stanie przejąć pewne funkcje

elementu uszkodzonego, choć mogą je realizować gorzej,

- parametryczne - własności fizyczne są „lepsze” od potencjalnie niezbędnych do

realizacji założonej funkcji, np. współczynniki bezpieczeństwa w budowie maszyn spełniają taką rolę,

- czasowe - uszkodzenie elementu nie powoduje natychmiastowej niezdatności

obiektu, dysponuje się pewnym czasem na podjęcie działań przeciwdziałających wystąpieniu uszkodzenia urządzenia jako całości.

Sposobem zwiększania niezawodności obiektów jest rezerwowanie zarówno całych obiektów jak i pojedynczych elementów, czy też grup elementów. W zależności od tego z jakim przypadkiem mamy do czynienia rozróżnia się rezerwowanie:

• globalne zwane również ogólnym,

• grupowe,

• jednostkowe zwane również indywidualnym,

• przesuwające się zwane również wędrującym.

Kryterium tak dokonanego podziału stanowi sposób przyporządkowania elementów rezerwowych elementom podstawowym.

Grupa rezerwowa - zespół elementów, który składa się z elementu podstawowego i elementów rezerwowych (co najmniej jednego). W niektórych przypadkach wyróżnienie elementu podstawowego ma charakter czysto umowny.

Biorąc pod uwagę stan w jakim znajdują się elementy rezerwowe, do chwili wystąpienia uszkodzenia elementu podstawowego, spośród wielu możliwych sposobów rezerwowania wyróżnia się następujące przypadki:

- rezerwa obciążona („gorąca”);

- rezerwa nieobciążona („zimna”),

- rezerwa częściowo obciążona („ciepła”).

• Rezerwa obciążona („gorąca”)

Element podstawowy „0” i rezerwowe od „1” do „n” poddawane są takim samym obciążeniom wynikającym z warunków pracy, zatem ich własności niezawodnościowe zmieniają się w taki sam sposób. Nie jesteśmy w stanie określić, który z elementów jest rezerwowy i który wcześniej ulegnie uszkodzeniu.

Czas zdatności urządzenia wyrazić można następującą zależnością:

• Rezerwa nieobciążona („zimna”)

Element podstawowy „0” pracuje, a rezerwowe „czekają” na uszkodzenie elementu pracującego. Zakładamy, że mamy do czynienia z idealnym przełącznikiem bezbłędnie rozpoznającym stan elementu podstawowego; czas przeznaczony na przełączenie uznajemy za pomijalnie mały. Zakładamy również, że własności niezawodnościowe elementów rezerwowych nie zmieniają się w czasie oczekiwania na włączenie do działania. Oznacza to, że element rezerwowy, w tym czasie nie starzeje się, nie jest poddawany obciążeniu i nie uszkadza się. Przyjmuje się, że czasy pracy elementów podstawowych i rezerwowych są wzajemnie niezależnymi zmiennymi losowymi.

Czas zdatności urządzenia wyrazić można następującą zależnością:

Rezerwa częściowo obciążona („letnia lub chłodna”)

Elementy rezerwowe w tym przypadku poddane są pewnemu obciążeniu w czasie oczekiwania na włączenie (jest to jednak obciążenie znacznie mniejsze niż elementu podstawowego). Zatem ich własności niezawodnościowe zmieniają się w tym czasie. Zachowanie elementu rezerwowego, gdy „zastąpi” on element podstawowy, będzie zależało od tego jak długo oczekiwał na pracę „pod pełnym obciążeniem”. Czasy zdatności poszczególnych elementów należy wówczas traktować jako zmienne zależne. Czas zdatności urządzenia wyrazić można następującą zależnością:

---