Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię Paweł Ignatowicz Studenta:							Instytut i symbol grupy MD103.1c
Data wykonania ćwiczenia: 06.01.2000		Symbol ćwiczenia: 9.1	Temat zadania: Pomiar rozkładu prędkości elektronów termoemisji.
Zaliczenie:			Ocena:	Data:	Podpis

1.Tabela pomiarów:

Lp	i = 290 mA		R = 10 k		V [m/s]	T [ K ]
		U [mV]	U [V]	i [ V]			[ ]
	0 -10 -20 -30 -40 -50 -60 -70 -80 -90 -100 -110 -120 -130 -140 -150 -180 -210 -240 -270	-0.7203 -0.6735 -0.6246 -0.5760 -0.5296 -0.4867 -0.4435 -0.4040 -0.3654 -0.3337 -0.3014 -0.2722 -0.2456 -0.2222 -0.2009 -0.1783 -0.1299 -0.0944 -0.0672 -0.0485	-72.03 -67.35 -62.46 -57.60 -52.96 -48.67 -44.35 -40.40 -36.54 -33.37 -30.14 -27.22 -24.56 -22.22 -20.09 -17.83 -12.99 -9.44 -6.72 -4.85	0.0000 3.1623 4.4721 5.4772 6.3246 7.0711 7.7460 8.3666 8.9443 9.4868 10.0000 10.4881 10.9545 11.4018 11.8322 12.2475 13.4164 14.4914 15.4919 16.4317	1,463 10	705,4

2.Obliczenia:

gdzie wartość R wynosiła 10 k

Wartość prędkości najbardziej prawdopodobnej elektronów :

V =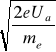

=
=0,351648352 10

V =
=

=1,875228924 10

V = 18752,28924

V = 18752,28924
7,8
= 1,463 10
m/s

Do obliczeń przyjmujemy następujące wartości stałych fizycznych:

e = 1,6 10
C

m
= 9,1 10
kg

k = 1,38 10
J/K

T =
705,3913044 K
705,4 K

3.Krótka teoria:

Zgodnie z teorią przewodnictwa

elektronowego, elektrony walencyjne tworzące gaz elektronowy, w temperaturze zera bezwzględnego obsadzają wszystkie najniższe poziomy energetyczne, aż po poziom odpowiadający energii Fermiego. Przy podwyższaniu temperatury metalu część elektronów przewodnictwa znajduje się na wyższych poziomach energetycznych i niektóre z nich opuszczają metal, zużywając przy tym część energii na pokonanie pracy wyjścia. Im wyższa jest temperatura metalu, tym większymi energiami dysponują elektrony przewodnictwa i tym większa ilość może pokonać barierę potencjału

i wydostać się na zewnątrz.

Zależność gęstości prądu termoemisji od temperatury ciała T emitującego elektrony przedstawia zależność otrzymana przez Richardsona:

gdzie:

1. stałą zależna od rodzaju materiału i stopnia czystości

1. ładunek elektronu

- potencjał wyjścia

11. stała Boltzmanna

Iloczyn oznacza pracę wyjścia.

Elektrony opuszczające powierzchnię katody mają początkowe prędkości , dlatego też nawet przy zerowym napięciu anodowym mogą pokonać pole hamujące ładunku przestrzennego, zgromadzonego wokół katody i dojść do anody. Przykładając do anody napięcie ujemne spowodujemy, że dobiegną do niej tylko te elektrony, których energie są na tyle duże aby pokonać działanie hamującego pola elektrycznego. Warunek ten można zapisać następująco:

gdzie:

m_e- masa elektronu

V- prędkość elektronu

U_a- wartość napięcia przyłożonego do anody.

Natężenie prądu płynącego w obwodzie anodowym lampy jest równe gdzie N_V jest liczbą elektronów docierających do anody w jednostce czasu, których prędkość spełnia warunek:

Zwiększając napięcie hamujące U_a powodujemy, że coraz mniejsza liczba elektronów N_V pokonuje pole hamujące i dobiega do anody. Fakt ten sprawia, że wartość natężenia prądu anodowego i_a maleje.

4.Schemat wykonania ćwiczenia:

Oznaczenia symboli:

Z₁, Z₂ - zasilacze

MC₁, MC₂ - mierniki cyfrowe

5.Opracowanie wyników pomiaru:

Opracowanie wyników pomiaru polegało na wykreśleniu charakterystyk:

Na podstawie otrzymanych charakterystyk wyznaczamy wartość napięcia U_a w celu wyznaczenia prędkości najbardziej prawdopodobnej elektronów. Wartość otrzymana z wykresu wynosi: 7,8, więc napięcie ma wartość 60,84mV.

Ze wzoru prędkość najbardziej prawdopodobna elektronów wynosi: .

Temperaturę katody wyznaczamy ze wzoru: . Wartość temperatury wynosi

Ponadto wyznaczono błąd względny maksymalny pomiaru wielkości V.

Ponieważ wartość prędkości zależy tylko od napięcia U_a (zmienna) stosując metodę różniczkową otrzymujemy:

Podstawiając wartości otrzymujemy: .

---