GAZY
Parametry gazu w warunkach normalnych
Po=101325 (Pa)
Vo=n*0,0224 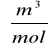
To=273K
Ciśnieniem nazywamy stosunek siły działającej prostopadle na daną powierzchnię do pola tej powierzchni oznaczamy je literą p
F- siła
s-pole powierzchni
p- ciśnienie
Jednostką ciśnienia jest paskal (p)=(N/m2)=(Pa) (paskal) paskalem nazywamy takie ciśnienie w którym na powierzchnię 1m2prostopadle do niej działamy siłą 1.
Inne jednostki ciśnienia:
atmosfera fizyczna oznaczenie atm
atmosfera techniczna oznaczenie at
bar oznaczenie B
Temperatura w Kelwinach nie przyjmuje wartości ujemnych należy pamiętać o tym, że 0˚C jest to 273˚K
Aby zamienić K na stopnie C musimy do temperatury w stopniach C dodać 273K.
T(K)= t˚(C) +273
Objętością molową gazu nazywamy stosunek objętości gazu do liczby moli zawartych w tym gazie.
V- objętość
n- objętość molowa gazu ![]()
Masą molową gazu nazywamy stosunek masy tego gazu do liczby moli zawartych w tym gazie.
μ=m/n |
μ =kg/mol |
Gęstością (masą właściwą ciała) nazywamy stosunek masy tego ciała do jego objętości
ϱ=m/v |
(ϱ)=(kg/m3) |
POJĘIE CIEPŁA WŁAŚCIWEGO
Ciepłem właściwym ciała nazywamy stosunek ciepła potrzebnego na ogrzanie tego ciała do jego masy i zmiany temperatury .
![]()
![]()
![]()
Ciepłem molowym nazywamy stosunek ciepła potrzebnego na ogrzanie tego ciała do liczby moli zawartych w tym ciele i zmiany temperatury
![]()
![]()
![]()
Połączenie ciepła molowego z właściwym
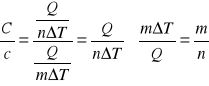
![]()
z tej zależności wynika, ze ciepło molowe ciała jest iloczynem jego ciepła właściwego i masy molowej
RÓWNANIE GAZU DOSKONAŁEGO
Podstawowy wzór teorii kinetycznej gazu
![]()
![]()
![]()
c- współczynnik temperatury
![]()
![]()
![]()
Jednostki:
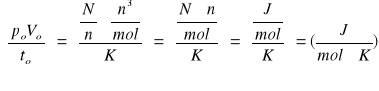
Po=101325(Pa)
Vo=n*0,0224(m3/mol)
To=273(K)
![]()
Równie gazu doskonałego z uwzględnieniem stałej gazowej R i liczby moli
![]()
Równanie gazu doskonałego z uwzględnieniem parametrów początkowych i końcowych tego gazu.
p1;V1;T1 - parametry początkowe
p2;V2;T2 -parametry końcowe
Równanie Clapeyrona jest równaniem gazu doskonałego które zostało przekształcone w sposób wygodniejszy do rozwiązania zadań, równanie to uwzględniać będzie masę molową gazu.
![]()
![]()
![]()
![]()
ZADANIA:
Oblicz objętość jaką zajmuje w temperaturze t=20˚, pod ciśnieniem p=106(Pa),1kg tlenu. Masa molowa tlenu wynosi μ=32g/mol.
Dane
V=?
t=20˚C=20˚C+273˚K=293˚K
p=106Pa
J=32g/mol=32*10-3kg/mol
R=8,31 J/mol
![]()
![]()
![]()
![]()
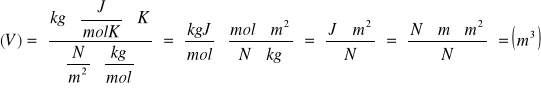
![]()
Korzystając z danych z poprzedniego zadania oblicz gęstość.
ϱ=?
![]()
![]()
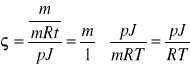
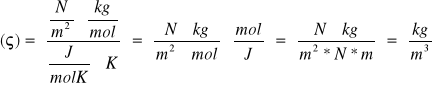
![]()
W naczyniach o objętości V=10-2m3 znajdują się m1=2g helu i m2=1g wodoru. Oblicz ciśnienie jakie panuje we wnętrzu naczynia jeżeli temperatura gazu wynosi 100˚C. Masa molowa gazu wynosi μ1=4g/mol a masa molowa wodoru μ2=2g/mol.
Dane
V=10-2 m3
m1=2 g=2*10-3 kg
m2=1 g=1*10-3 kg
t=100˚C=373 (K)
μ1=4 g/mol=4*10-3 kg/mol
μ2=2 g/mol=2*10-3 kg/mol
R=8,31 J/mol
![]()
![]()
![]()
![]()
![]()
![]()
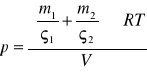
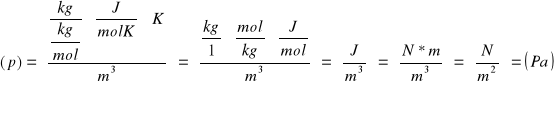
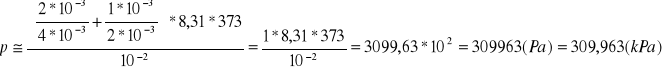
Korzystając z zależności ciśnienia od temperatury sporządzonej dla helu wyznacz jego objętość zakładając, że masa helu wynosi m=2. masa molowa helu wynosi μ=4 g/mol.
Dane:
V=?
m=2g=2*10-3 kg
μ=4 g/mol=4*10-3 kg/mol
R=8,31 J/mol ![]()
dla T=400K
to p=40*103
![]()
![]()
![]()
![]()
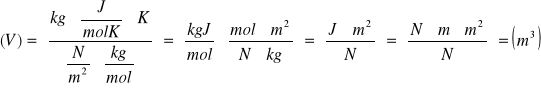
![]()
W naczyniach o jednakowych objętościach znajdują się równe masy helu i orgonu. Ile razy ciśnienie helu jest większe od ciśnienia orgonu, jeżeli temperatura obu gazów są identyczne? Masa molowa helu wynosi μ1=4g/mol, a masa molowa orgonu μ2=40g/mol.
Dane
![]()
![]()
μp=4g/mol=4*10-3 kg/mol
μa=40g/mol=40* 10-3 kg/mol
Vh=Va
![]()
![]()
![]()
![]()
/:Vμ
![]()
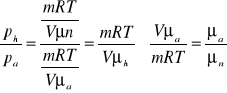
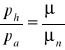
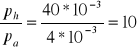
Ciśnienie helu jest 10 razy większe niż ciśnienie orgonu.
PRZEMIANY GAZOWE
![]()
m- const; T- const przemiana izotermiczna
m- const; p- const przemiana izobaryczna
m- const; V-const przemiana izochoryczna
n- const; Q- const przemiana adiabatyczna (nie ma wymiany ciepła z otoczeniem)
Przemianą izotermiczną stałej masy gazu nazywamy taką przemiane gazu doskonałego której temperatura jest wielkością stałą.
m-const T- const
Wprowadzając równanie przemiany izotermicznej wykorzystamy równanie przemiany izotermicznej parametrów początkowych i końcowych gazu.
![]()
T1=T2=T3=const
![]()
/*T
![]()
pV=const jest to równanie izotermy opisujące prawo Boyle'a Mariott'a
Prawo to mówi, że w przemianie izotermicznej stałej masy gazu iloczyn objętości i ciśnienia jest wielkością stałą.
Przemianą izobaryczną stałej masy gazu nazywamy taka masę gazu doskonałego w której ciśnienie jest wielkością stałą
m-const p- const
![]()
![]()
![]()
![]()
![]()
Wzór przemiany izobarycznej który opisuje prawo Gay Lusaca prawo to brzmi przemiany izobarycznej stałej masy gazu objętość jest wprost proporcjonalna do temperatury wyrażonej w Kelwinach
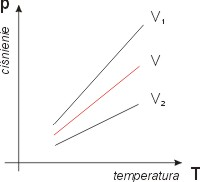
Przemianą izochoryczną stałej masy gazu nazywamy taką przemianę gazu doskonałego której odętość jest wielkością stałą
m=const; V=const
![]()
![]()
równanie przemiany izochorycznej,
które opisuje prawo Charlesa
Prawo brzmi w przemianie izochorycznej stałej masy gazu cieśninie jest wprost proporcjonalne do temperatury wyrażonej w Kelwinach.
2 mole tlenu poddano przemianie 1-2 której przebieg przedstawiono na rysunku. Parametry początkowe tlenu wynoszą p1=105(Pa) i V1=0,1(m3). Oblicz temperaturę końcową tlenu.
n=2mole
p1=105(Pa)
V1=0,1(m3)
![]()
![]()
![]()
![]()
Wzór
![]()
Obliczenia
![]()
Jednostki
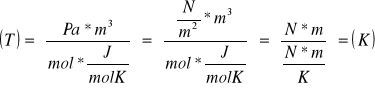
W jednakowych balonach i w jednakowej temperaturze znajdują się równe masy wodoru i dwutlenku węgla w ścianki balonu. Masy molowe wynoszą odpowiednio μ=2g/mol oraz μ=44g/mol.
T1=T2=T
![]()
![]()
![]()
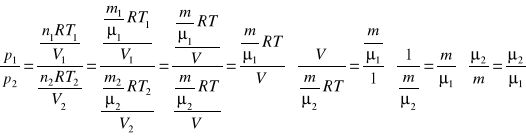
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
624
624
di 624+ qig pl pjktouxg6qsmjksgto6db5ukkli5cjomydcaowy PJKTOUXG6QSMJKSGTO6DB5UKKLI5CJOMYDCAOWY
624
624
624
44 611 624 Behaviour of Two New Steels Regarding Dimensional Changes
gewis kolos 3 624, GEWiS
Akumulator do?RRARI@624@624
624 3 70
624
624
624
624
624 625
624
624
624
więcej podobnych podstron