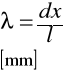PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA w PILE
INSTYTUT POLITECHNICZNY
KATEDRA BUDOWY I EKSPLOATACJI MASZYN
SPRAWOZDANIE
z ćwiczenia laboratoryjnego
nt. „Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej”
WYKONAŁ |
GRUPA |
DATA |
OCENA |
Adam Koper Krzysztof Jiers |
I |
17.03.2002 |
|
Spis teści:
Wstęp
Cel ćwiczenia
Przebieg ćwiczenia
Tabela wyników pomiarów
Wnioski
Wstęp
Siatkę dyfrakcyjną stanowi szereg szczelin umieszczonych w równych od siebie odległościach w nieprzeźroczystym ekranie. W praktyce siatkę dyfrakcyjną otrzymuje się najczęściej przez porysowanie płasko-równoległej płytki szklanej za pomocą diamentu szeregiem równoległych kresek.
Nieprzeźroczyste rysy odgrywają rolę zasłon, a przestrzenie między rysami - to szczeliny.
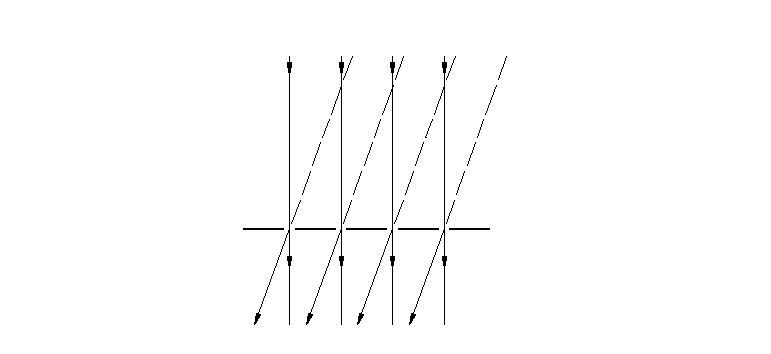
Jeśli na siatkę dyfrakcyjną prostopadle do jej powierzchni pada wiązka promieni równoległych, to - zgodnie z zasadą Huygensa - każda szczelina staje się źródłem drgań i wysyła promienie we wszystkich kierunkach, a więc nie tylko w kierunku promieni padających.
Zjawisko to nazywa się dyfrakcją, czyli uginaniem prostoliniowego biegu promieni. Promienie ugięte mogą nakładać się, czyli interferować ze sobą, gdyż są promieniami spójnymi: znaczy to, że różnice faz między nimi zależą tylko od różnic dróg geometrycznych, nie zależą zaś od czasu.
Biorąc pod uwagę wiązki promieni ugiętych zauważyć można, że w pewnych kierunkach promienie te będą się wzmacniały, w innych zaś - wygaszały (częściowo lub zupełnie).
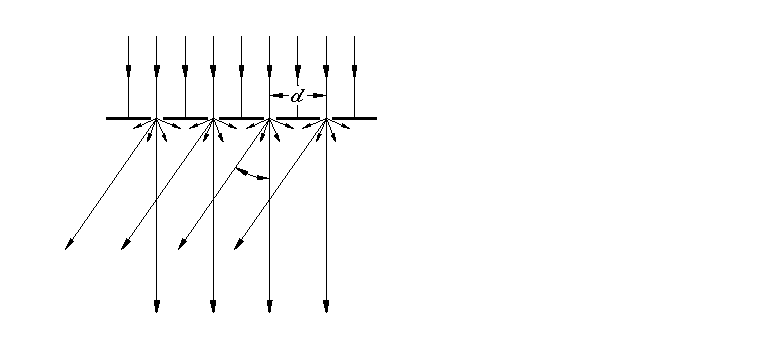
Promienie ugięte będą się wzmacniać, jeśli różnice dróg dwóch sąsiednich promieni będą równe całkowitej wielokrotności długości światła padającego (Rys. 1)
Warunek wzmocnienia promieni ugiętych na siatce dyfrakcyjnej ma postać
![]()
d - stała siatki - odległość między sąsiednimi szczelinami
n -rząd widma (n może być równe 1, 2, 3, ....)
Przy każdej wartości długości fali l oraz przy każdym n - kąt wzmacniania się promieni ugiętych jest inny, a więc kierunki wzmacniania promieni różnych barw są różne.
W wyniku tego obserwujemy następujące zjawisko:
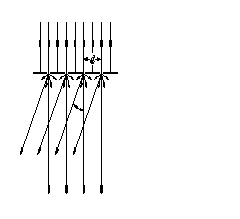
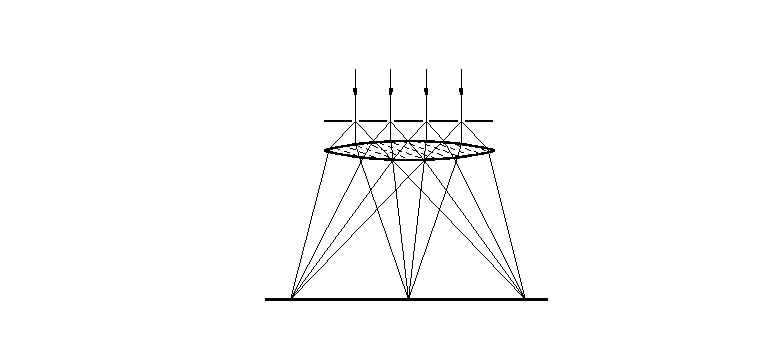
Jeśli poza siatką dyfrakcyjną na którą pada wiązka promieni równoległych umieścimy soczewkę zbierającą, a w pewnej odległości od niej ekran - to powstaną na nim oprócz smugi odpowiadającej promieniom nie ugiętym po jej obu stronach barwne widma (Rys. 2).
Schemat doświadczalny przedstawiony na Rys. 2 można zmienić umieszczając na miejscu soczewki oko obserwatora, co miało miejsce w naszym przypadku.
Soczewka oczna wytworzy na siatkówce obraz promieni ugiętych. Obserwator wyobrazi sobie, że na przedłużeniu wiązek ugiętych znajdują się barwne źródła światła (Rys. 3).
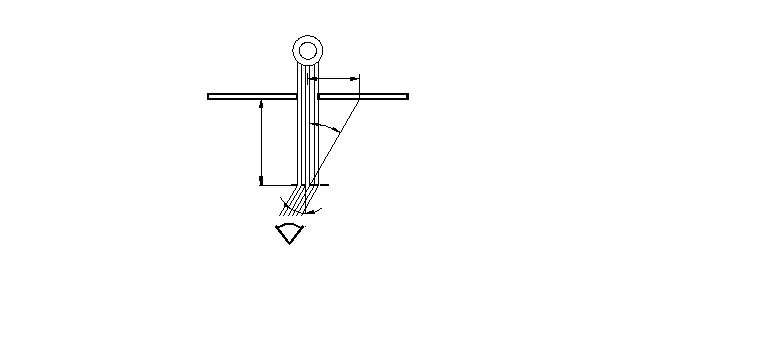
W oparciu o powyższe rozważania możemy wyznaczyć długość fali świetlnej posługując się następującym urządzeniem (Rys 4).
Lampa L (dająca widmo liniowe, najczęściej lampka neonowa) wysyła przez wąską prostokątną szczelinę w ekranie E wiązkę promieni w przybliżeniu równoległych.
Znajdujące się poza siatką dyfrakcyjną S oko obserwatora ujrzy na ekranie E szereg barwnych prążków z prawej i lewej strony szczeliny.
Jest to widmo pozorne, widziane przez obserwatora na tle ekranu na przedłużeniu wiązek ugiętych wchodzących do oka.
Zależnie od wielkości stałej siatki możemy obserwować na ekranie 1, 2, lub nawet kilka rzędów widm.
Cel ćwiczenia
Celem ćwiczenia jest wyznaczenie długości fal świetlnych przy użyciu siatki dyfrakcyjnej
Przebieg ćwiczenia
Aby wyznaczyć długość światła linii obserwowanej na ekranie musimy znać odpowiadający jej kąt ugięcia, dający wzmocnienie fali świetlnej danej barwy.
Kolejność czynności
Umieszczamy siatkę dyfrakcyjną o stałej d=1,7mm na statywie - równolegle do ekranu (dsinα=nλ
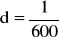
mm)Spoglądamy przez siatkę na ekran i obserwujemy barwne prążki.
Za pomocą miary dokonujemy pomiaru xc dla barwy czerwonej, xf dla barwy fioletowej oraz xz dla barwy zielonej (Rys. 5).
4. Tabela wyników pomiarów
Tabela nr.1
Lp |
Stała siatki d [mm] |
Barwa |
Odległość między prążkami na ekranie x [mm] |
Odległość siatki od ekranu l [mm] |
|
1 |
1,7 |
Fiolet |
80 |
300 |
0,000444 |
2 |
1,7 |
Zieleń |
95 |
300 |
0,000527 |
3 |
1,7 |
Czerwień |
110 |
300 |
0,000611 |
|
|||||
B. Obliczenia
Fiolet
Zielony
Czerwony
TABELA DŁUGOŚCI FAL
Tabela nr.2
BARWA |
DŁUGOŚĆ FALI |
Fiolet |
0,40 - 0,45 μm |
Zieleń |
0,49 - 0,56 μm |
Czerwień |
0,61 - 0,70 μm |
Obliczamy niepewność pomiarową:
δx=λ(d+x+l)
λ= ± δx
FIOLET
ZIELEŃ
CZERWIEŃ
Tabela nr.3
BARWA |
DŁUGOŚĆ FALI μm |
FIOLET |
0,444 ± 0,006 μm |
ZIELONY |
0,527 ± 0,008 μm |
CZERWIEŃ |
0,611 ± 0,008 μm |
5. WNIOSKI :
Porównując wyniki zawarte w tabeli nr.2 z wynikami otrzymanymi w obliczeniach podczas wykonywania doświadczenia - (tabela nr.3) możemy stwierdzić, że całe doświadczenie zostało wykonane prawidłowo, gdyż wyniki są porównywalne.
FIZYKA
Str.1
PIŁA 2002
wiązka pierwotna
Rys.1
α
wiązka
ugięta
wiązka nieugięta
soczewka
zbierająca
ekran
Rys. 2
Rys. 3
Kierunek, w którym obserwator widzi pozorne źródło światła
Oko
Oko
x1
l
E
S
L
α
α
Rys. 4
Rys. 5
Xf
Xz
Xc
![]()
![]()
![]()
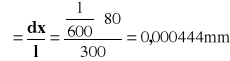
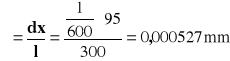
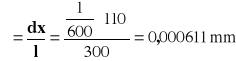
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Fizyka II s. Elektrostatyka 2, mechanika, BIEM- POMOCE, laborki z fizy, moje, laboratorium z fizyki,
lab ćw3, mechanika, BIEM- POMOCE, laborki z fizy
cin2, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
lab ćw.4, mechanika, BIEM- POMOCE, laborki z fizy
lab ćw2, mechanika, BIEM- POMOCE, laborki z fizy
piknometr, mechanika, BIEM- POMOCE, laborki z fizy
cin4, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
lab ćw8, mechanika, BIEM- POMOCE, laborki z fizy
lab ćw5, mechanika, BIEM- POMOCE, laborki z fizy
lab ćw8tomasz, mechanika, BIEM- POMOCE, laborki z fizy
Rachunek bledow wyznaczanie gestosci hydro, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
wyznaczanie predkosci fal dzwiekowej, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
cin3, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
Sprawozdanie z fizyki nr4, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
Fizyka II s. Elektrostatyka 1, mechanika, BIEM- POMOCE, laborki z fizy, moje, laboratorium z fizyki,
Zestawiamy transformator 900, mechanika, BIEM- POMOCE, laborki z fizy
STR1, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
Pracownia fizyczna - instrukcja, mechanika, BIEM- POMOCE, laborki z fizy
więcej podobnych podstron