Akademia Techniczno-Humanistyczna w Bielsku-Białej

Wydział: NoMiŚ

Kierunek: Inżynieria Środowiska

Rok akademicki: 2012/2013

Semestr: II

ĆWICZENIE 40

Temat: Zastosowanie metody Stokesa do badania wpływów temperatury na lepkość cieczy.

Wykonała grupa 107
w składzie:

agentki

1.Wiadomości teoretyczne

a) Lepkość

Z lepkością cieczy związana jest tzw. siła oporu lepkiego. Jest to siła, z jaką działają na siebie kolejne warstwy poruszającej się cieczy, której wektor styczny jest do powierzchni warstw.

Rys.1. Warstwowy przepływ cieczy lepkiej.

Wzór Newtona pozwalający wyznaczyć wartość siły oporu lepkiego cieczy nieściśliwej ma postać:

,

gdzie: η - dynamiczny współczynnik lepkości cieczy [Ns/m² = kg/ms]

- gradient lepkości w kierunku osi Z

ΔS - pole powierzchni warstw cieczy

Do scharakteryzowania własności cieczy lepkich stosuje się także kinematyczny współczynnik lepkości v:

,

gdzie: ρ - gęstość cieczy lepkiej

Ciekawym zjawiskiem jest spadek współczynnika lepkości η wraz ze wzrostem temperatury. Wyjaśnia się to w ten sposób, iż lepkość cieczy związana jest z koniecznością pokonywania przez cząsteczki cieczy pewnej bariery energetycznej E między cząsteczkami podczas ruchu. Jako, że temperatura to nic innego, jak energia kinetyczna cząsteczek - jej wzrost ułatwia pokonanie bariery energetycznej. Wpływ temperatury na współczynnik lepkości określa się zależnością ekspotencjalną

,

gdzie: k = 1,3805 ∙ 10^-23 [J/K] jest stałą Boltzmana

T - temperatura w skali bezwzględnej Kelvina

Ze względu na charakter przepływu można wyróżnić dwa rodzaje ruchów cieczy:

• Ruch laminarny (warstwowy) charakterystyczny dla cieczy poruszających się z małą prędkością; jego cechą jest ruch w równoległych warstwach, brak składowych poprzecznych ruchu i związanego z tym mieszania się warstw;

• Ruch turbulentny (wirowy) typowy dla cieczy o dużej prędkości przepływu; jest to ruch nieuporządkowany, w którym niemożliwe jest rozróżnienie poszczególnych warstw.

Rozróżnienie tych dwóch ruchów dokonuje się poprzez wyznaczenie tzw. liczby Reynoldsa

,

gdzie: V - średnia prędkość przepływu cieczy w kanale

D - średnica kanału

Dla wartości Re > 2300 przepływ uznawany jest za turbulentny, dla Re < 2300 za laminarny.

b) Ruch ciała w cieczy lepkiej

Ciało stałe poruszające się wewnątrz cieczy wywołuje w niej ruchy warstw cieczy. Warstwa znajdująca się najbliżej ciała będzie poruszać się z taką samą prędkością jak to ciało, a warstwy dalsze z coraz mniejszą prędkością ze względu na siłę oporu lepkiego. Siła ta zależy od gradientu prędkości w kierunku prostopadłym do ruchu, lepkości cieczy oraz kształtu ciała. Wartość tej siły dla kuli opisana jest wzorem Stokesa

,

gdzie: T - siła oporu lepkiego

η - dynamiczny współczynnik lepkości cieczy

r - promień kuli

v - prędkość kuli

Rys.2. Rozkład prędkości warstw cieczy wokół kuli poruszającej się w cieczy lepkiej.

Równanie ruchu dla kuli o masie m i promieniu r, opadającej pod wpływem własnego ciężaru w cieczy lepkiej o lepkości η i gęstości ρ będzie miało postać

,

a jego rozwiązaniem jest zależność prędkości kuli od czasu postaci

,

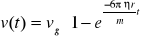
gdzie: v_g - graniczna prędkość ruchu jednostajnego kuli, z jaką będzie ona opadała po wytworzeniu się równowagi pomiędzy siłą ciężkości Q, siłą wyporu F_wyp i siłą Stokesa T(v_g).

Z warunku równowagi sił ( Q = F_wyp + T(v_g) ) wynika prędkość graniczna równa

,

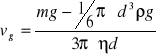
gdzie: d - średnica kuli (równa 2∙r),

co oznacza, że przy równowadze sił lepkość cieczy, w której kula przebyła drogę l w czasie t wynosi

.

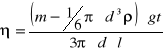
Rys.3. Układ sił działających na kulkę opadającą w cieczy lepkiej.

2. Przebieg ćwiczenia:

• Aby wykonać ćwiczenia użyłyśmy Wiskozymetru Stokesa (rys.4) wypełnionego gliceryną, ultra termostatu wyposażony w termometr do pomiaru temperatury wody ogrzewającej wiskozymetr, śruby mikrometrycznej, wagi laboratoryjnej i wagi analitycznej, stopera i kulek stalowych (35 sztuk).

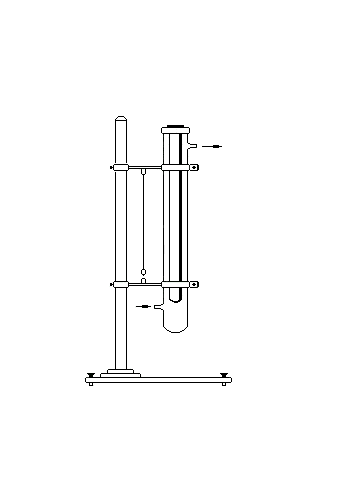
Rys.4. Wiskozymetr Stokesa

• Następnie wybrałyśmy w sposób losowy dziesięć kulek. Dokonałyśmy pomiaru ich masy, wpierw na wadze laboratoryjnej, później natomiast uściśliłyśmy pomiar za pomocą wagi analitycznej, ważąc kulki kolejno z nadmiarem i niedomiarem, a później wyliczając wagę średnią każdej z kulek. Obliczyłyśmy średnią masę kulki i oszacowałyśmy błąd pomiaru a wyniki umieściłyśmy w tabeli. Obliczyłyśmy średnią średnicę d kulki (d =Σd_i / 10), średni błąd kwadratowy pojedynczego pomiaru S_d skorygowany przez odpowiedni współczynnik Studenta - Fischera: S_d=S'_d·t_α,n

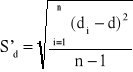
oraz błąd pomiaru średnicy Δd:

Δd = (S_d² + 0.0001)^1/2 mm.

• Na podstawie tabeli przedstawiającej gęstość roztworu wodnego gliceryny ( 86% ) w funkcji temperatury, obliczyłyśmy gęstość gliceryny w temperaturze początkowej.

T [°C]	15	20	21,6	25	30	35	40	45	50
ρ [10 kg^3/m^3]	1.225	1.221	1261,12	1.220	1.216	1.213	1.211	1.208	1.205

Przeszłyśmy do pomiarów zasadniczych. Pomiary zasadnicze składają się z siedmiu serii pomiarowych. Pierwsza wykonywana jest w temperaturze otoczenia T₁, a następne pięć serii pomiarów po ogrzaniu gliceryny o: 5, 10, 15, 20, 25 °C, licząc od temperatury otoczenia. Ostatnią (siódmą) serię pomiarów należy wykonać przy temperaturze nie wyższej niż 55 °C. W każdej serii pomiarowej wykorzystuje się pięć kulek.

Po wykonaniu pomiarów ich wyniki również umieściłyśmy w tabeli. Następnie otrzymane wyniki wprowadziłyśmy do programu komputerowego, uzyskując wyniki i ich graficzne przedstawienie w formie wykresu.

Wyniki pomiarów:

Tab. 1

Nr pomiaru	Temperatura [^oC]	Temperatura [K]	1/T [1/K^-1]	t1 [s]	t2 [s]	t3 [s]	t4 [s]	t5 [s]	<t> [s]
1	20.6	293.75	0,0034	5,77	5,88	5,88	5,88	5,85	5,85
2	25.0	298,15	0,0034	4,49	4,44	4.43	4,37	4,34	4,41
3	30.0	303,15	0,0033	3,64	3,42	3.47	3,42	3,43	3.48
4	35.0	308,15	0,0032	2,78	2,74	2,76	2,78	2,78	2,77
5	40.0	313,15	0,0032	2,36	2,37	2.37	2.48	2.36	2.39
6	45.0	318,15	0,0031	2,06	2,13	2.03	2.16	2.03	2,08
7	50.0	323,15	0,0031	1,86	1,82	1,80	1,77	1,89	1,83

Tab. 2

d1 [10^-3m]	d2 [10^-3m]	d3 [10^-3m]	d4 [10^-3m]	d5 [10^-3m]	<d> [10^-3m]	Sd [10^-3m]	Δd [10^-3m]
2.50	2.49	2.49	2.50	2.50	2.50	0.0085	0.04

Przykład obliczeń:

Średnią wartość średnicy kulki obliczyłyśmy ze wzoru:

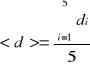
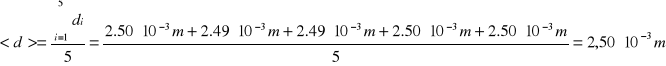
Średni błąd kwadratowy pojedynczego pomiaru średnic Sd ze wzoru:

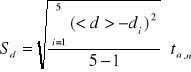
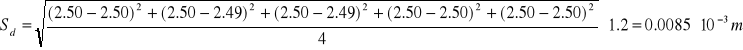
Współczynnik studenta przyjęłyśmy
= 1.2

Błąd bezwzględny pomiaru średnicy kulki:

Energia aktywacji przepływu lepkiego:

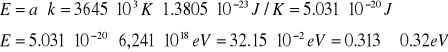
Błąd bezwzględny energii aktywacji:

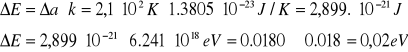
Obliczenia dla t = 25 ^oC

T = t + 273,15K

T = 25 +273 = 298,15 K

1 / T = 1 / 298K = 0.0034 K^-1

d=1220 [kg/m³]

współczynnik lepkości dynamicznej:

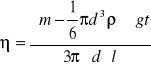
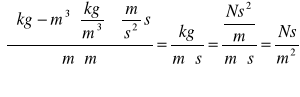
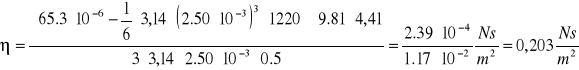
Błąd współczynnika:

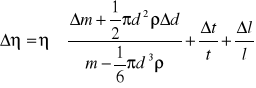
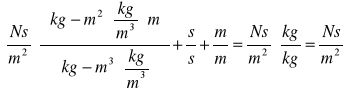
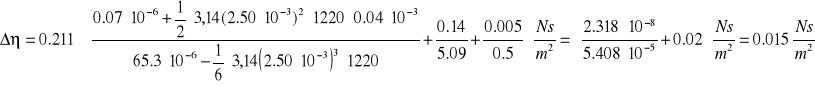
Teoretyczne wartości _t

Do wyznaczenia η_t potrzebujemy wartości η₀ . Wyznaczamy ja ze wzoru:

Stąd wyznaczamy wartości η_t dla poszczególnych temperatur (przykładowo dla T = 298 K)

Wyniki obliczeń:

Tab. 3

nr pomiaru	T [K]	1/T*[k^-1*10^-4]	η [Ns/m^2]	Δη [Ns/m^2]	lnn [-]	ηt [Ns/m^2]
1	295.6	33.98	0.269	0.0176	-1.312	0.24
2	298	33.93	0.203	0.0159	-1.594	0.20
3	303	33.54	0.160	0.0154	-1.832	0.16
4	308	32.45	0.127	0.0131	-2.060	0.12
5	313	31.93	0.110	0.0129	-2.207	0.10
6	318	31.43	0.096	0.0127	-2.344	0.08
7	323	30.94	0.084	0.0121	-2.473	0.07

Wnioski:

Wraz ze wzrostem temperatury cieczy, zaobserwowałyśmy dostrzegalną zmianę tępa spadania kulek. W miarę jak temperatura rosła, czas spadania skracał się - można stąd wywnioskować, że zmniejszeniu ulegała gęstość cieczy hamująca proces opadania kulek. Wynika to z faktu, że ze wzrostem temperatury rośnie energia kinetyczna cząsteczek i łatwiej mogą one pokonywać barierę potencjału oddziaływań międzycząsteczkowych ΔE, występującą pomiędzy sąsiadującymi ze sobą cząsteczkami.

---