Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię Huk Tomasz studenta:							Symbol grupy MD 103.1c
Data wykonania ćwiczenia:		Symbol ćwiczenia: 2.1	Temat zadania: Wyznaczanie współczynników osłabienia promieniowania .
Zaliczenie:			Ocena:	Data:09.12.99	Podpis

1. WYNIKI POMIARÓW I OBLICZEŃ

-pomiar tła

Lp.	t [s]	N
1	200	30921	31006
2				31130
3				30968

-pomiar płytek stalowych

Lp.	x [cm]	N	t [s]	N - [1/s]	ln(N - )	[mm]	[ ]	x [ ]	[m]	[ ]
1	0	234310	200	203304	12,22	0,064	8,11	10,8	64,17	8,1331
2	9,14	148522			117516						11,67
3	18,36	99335			68329						11,13
4	27,48	71435			40429						10,61
5	36,58	54784			23778						10,08
6	40,86	49050			18044						9,80
7	50	41946			10940						9,30
8	59,12	36866			5860						8,67
9	68,28	34903			3897						8,27
10	77,38	33168			2162						7,68
11	86,66	31930			924						6,83
12	95,8	31647			641						6,46
13	105	31264			258						5,55
14	114,14	31103			97						4,57

2.OBLICZENIA.

=
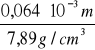
=0,008111534
= 8,11

- gęstość stali = 7,89 g/cm

- grubość połówkowego osłabienia
=


=
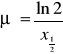
64,17m
=
=8,133079848

3.KRÓTKA TEORIA.

Promieniowanie γ jest to promieniowanie elektromagnetyczne powstające przy przejściu jądra ze stanu wzbudzonego do stanu do stanu o niższej energii, którym może być zarówno stan podstawowy jak i wzbudzony. Energie wzbudzenia jądra mogą przyjmować tylko ściśle określone wartości, zatem widmo energetyczne kwantów γ jest widmem liniowym. Promieniotwórczym rozpadom jąder towarzyszy zwykle emisja kwantów γ  energiach od 10keV do 5MeV.

Dominującymi procesami w oddziaływaniu z materią są: zjawisko fotoelektryczne, zjawisko Comptona, zjawisko tworzenia par elektrono-pozytonowych.

W zjawisku fotoelektrycznym kwant γ przekazuje całą swoją energię związanemu elektronowi, który uzyskuje energię Trówną:

T=h-I

gdzie I jest energią wiązania elektronu na odpowiedniej powłoce. Elektron może być wyrzucony z absorbentu, lub jeśli absorbent nie jest zbyt cienki, może być w nim natychmiast zaabsorbowany. Ze względu na zasadę zachowania pędu zjawisko zjawisko fotoelektryczne nie może zachodzić na elektronach swobodnych. Może zachodzić tylko na elektronach związanych.

Zjawisko Comptona jest to sprężyste zderzenie kwantu γ z elektronem swobodnym lub słabo związanym. W jego wyniku powstaje rozproszony kwant γ o mniejszej energii oraz obdarzony częścią energii kwantu pierwotnego, tzw. elektron komtonowski. Długość fali γ promieniowania rozproszonego w zjawisku Conptona możnz obliczyć ze wzoru;

gdzie:

h- stała Plancka

m_e- masa spoczynkowa elektronu

c- prędkość światła

- kąt rozproszenia kwantu

- długość fali promieniowania pierwotnego

Trzecim z podstawowych rodzajów oddziaływania promieniowania γ z materią jest proces tworzenia par: elektron-pozyton. Zachodzi w polu elektrycznym jądra lub elektronu a polega na przemianie kwantu γ w elektron i pozyton. Ze względu na konieczność równoczesnego spełnienia praw zachowania energii i pędu, utworzenie pary e^- i e⁺ w próżni nie jest to możliwe. Para może powstać tylko w obecności trzeciej cząstki: jądra lub elektronu.

W przypadku granicznym pozyton i elektron mogą mieć energię kinetyczną równą zero. Wtedy energia progowa tworzenia pary wynosi:

h_pr=2m_ec²+T_k

gdzie T_k jest energią odrzutu jądra lub elektronu, w obecności którego powstaje para.

Podstawową cechą charakterystyczną oddziaływania promieniowania γ z materią jest występowanie tzw. zjawiska śrubowego, polegającego na tym że każdy foton jest niezależnie usuwany z padającej wiązki promieniowania. Liczba kwantów dN usuniętych ze strumienia o natężeniu N, po przejściu przez warstwę absorbentu o grubości wynosi:

dN = -  dx

gdzie  jest stałą dla określonej energii promieniowania γ oraz ośrodka i nazywa się współczynnikiem osłabienia. Po scałkowaniu:

gdzie:

N₀-natężenie promieniowania padającego na absorbent

14. natężenie promieniowania po przejściu przez absorbent o grubości x

Współczynnik osłabieni jaką część strumienia promieniowania zostanie usunięta z wiązki pierwotnej po przejściu przez warstwę absorbentu o jednostkowej grubości. Jeśli grubość absorbentu wyrazimy w jednostkach długości to mówimy o liniowym współczynniku osłabienia, jeśli zaś w jednostkach masy na jednostkę powierzchni, mówimy wtedy o masowym współczynniku osłabienia.

Wykładnicza postać prawa osłabienia pozwala w prosty sposób wyznaczyć współczynnik osłabienia:

LnN = lnN_o -  x

4.SCHEMAT ĆWICZENIA I OPIS WYKONANIA.

P. A O

SS *Z

UL

Rys. Zestaw do pomiaru Współczynnika osłabienia promieniowania γ

O- osłona ołowiana z kolimatorem ,

Z- źródło promieniowania,

P.- pręt do zawieszania płytek absorbentu,

A- płytki absorbentu,

SS- detektor scyntylacyjny,

UL.- układ zasilający.

Źródło promieniowania znajduje się w osłonie ołowianej. Promieniowanie przechodzi przez kolimator i pada na absorbent zawieszony na pręcie. Po przejściu przez absorbent rejestrowana jest przez detektor i układ zasilający.

Pomiary polegają na rejestracji kwantów γ przechodzących przez absorbent (ołów) o zmiennej grubości (grubość płytek absorbentu 5 i 10 mm).

Pierwszym pomiarem jest pomiar tła promieniowania. W tym celu należ pomiędzy źródłem promieniowania , a sondą umieścić wszystkie płytki ołowiane i rejestrować liczbę zliczeń impulsów w ustalonym przedziale czasu (200s.). Następnym pomiarem jest pomiar bez absorbentu. Później dokładamy po jednej płytce i każdorazowo rejestrujemy liczbę zliczeń impulsów, aż do osiągnięcia poziomu tła promieniowania.

5.OPRACOWANIE WYNIKÓW POMIARÓW.

Lp.	x mm	N - [1/s]	ln(N - )	x^2 mm^2	xy mm	w -	=a mm	b=lnN0 -	N0 1/s
1	0	203304	12,22	0	0	1
2	9,14	117516	11,67	83,54	106,57	1
3	18,36	68329	11,13	337,09	204,35	1
4	27,48	40429	10,61	755,15	291,56	1
5	36,58	23778	10,08	1338,09	368,73	1
6	40,86	18044	9,80	1669,54	400,43	1	-0,064	6,889	981,42
7	50	10940	9,30	2500	465	1
8	59,12	5860	8,67	3495,17	512,57	1
9	68,28	3897	8,27	4662,16	564,67	1
10	77,38	2162	7,68	5987,66	594,28	1
11	86,66	924	6,83	7509,95	591,89	1
12	95,8	641	6,46	9177,64	618,87	1
13	105	258	5,55	11025	582,75	1
14	114,14	97	4,57	13027,94	521,62	1
	=788,8		=122,84	=61568,93	=5823,29	14

,

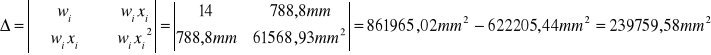
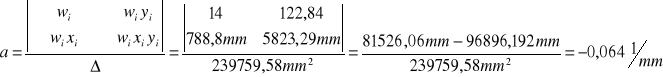
Lp.	xi mm	b 1/mm	 1/mm	y' -	y -	y=y'-y -	y^2 -	a 1/mm	b
1	0			12,39	12,22	0,17	0,0289
2	9,14			11,80	11,67	0,13	0,0169
3	18,36			11,21	11,13	0,08	0,0064
4	27,48			10,63	10,61	0,02	0,0004
5	36,58			10,05	10,08	-0,03	0,0009
6	40,86	12,39	0,064	9,77	9,80	-0,03	0,0009
7	50			9,19	9,30	-0,11	0,0121	0,0016	0,0108
8	59,12					8,61	8,67			-0,06	0,0036
9	68,28			8,02	8,27	-0,25	0,0625
10	77,38			7,44	7,68	-0,24	0,0576
11	86,66			6,84	6,83	0,01	0,0001
12	95,8			6,26	6,46	-0,20	0,04
13	105					5,67	5,55			0,12	0,0144
14	114,14					5,08	4,57			0,51	0,2601
							=0,5048

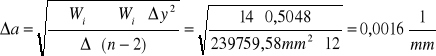
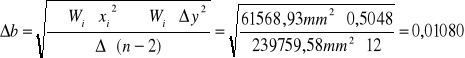
Równanie wyznaczonej prostej zapiszemy w postaci: .

Błąd względny wyznaczania współczynnika osłabienia ma wartość: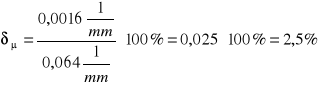
.

Błąd względny wyznaczania liczby zliczeń wynosi:
.

ln

ln

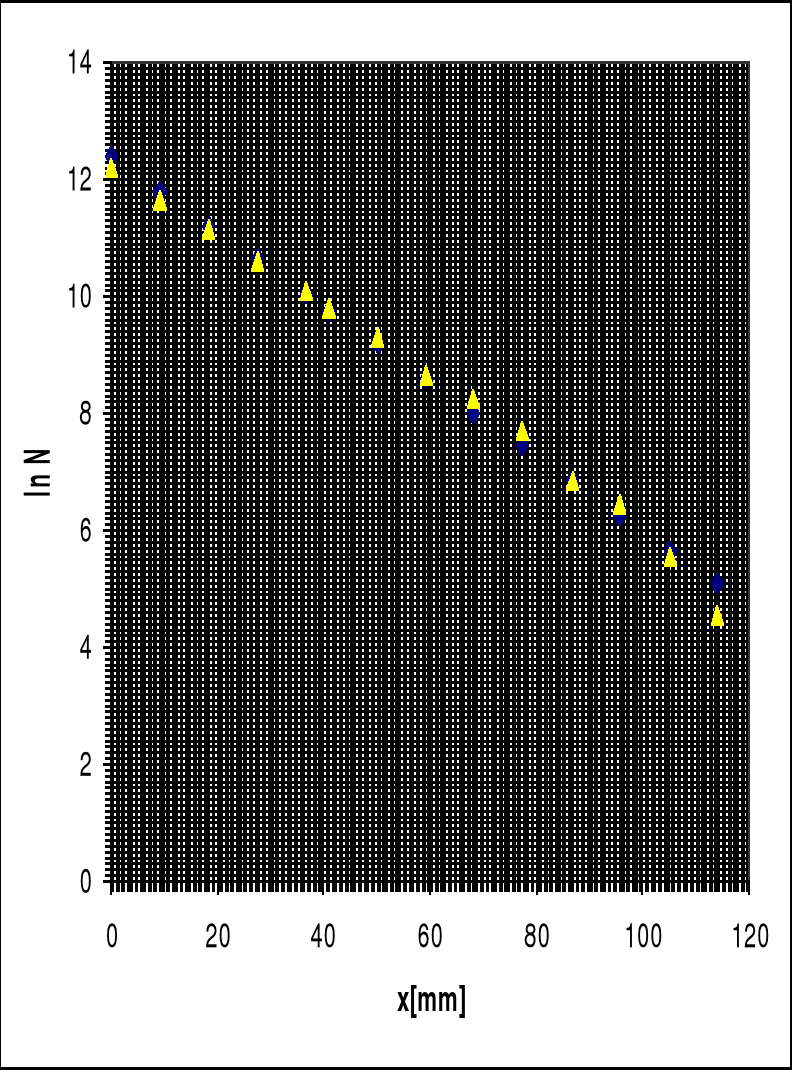
Z wykresu dla wartości 11,67 odczytujemy wartość : x
= 10,8 mm

=
=
=

=

=
=

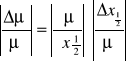
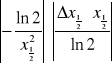
1

6

---