Politechnika Lubelska |
Laboratorium fizyki |
|||
|
Ćwiczenie nr 8.1 |
|||
Nazwisko i imię Stolarz Robert |
Semestr Trzeci |
Grupa
ED 3.3
|
Rok akadem.
1999/00
|
|
Temat ćwiczenia Wyznaczanie współczynnika napięcia powierzchniowego cieczy metodą kapilary pionowej |
Data wykonania
|
Podpis prowadzącego
|
||
1.Napięcie powierzchniowe cieczy
Cząsteczki cieczy podlegają działaniu sił wzajemnego przyciągania, zwanych siłami spójności. Siły te działają tylko między sąsiednimi cząsteczkami i są krótkozasięgowe. Siły spójności działające na cząsteczkę znajdującą się wewnątrz cieczy wzajemnie się kompensują. Cząsteczki znajdujące się w warstwie powierzchniowej cieczy podlegają działaniu sił spójności tylko ze strony cząsteczek leżących wewnątrz; wypadkowa tych sił jest różna od zera i skierowana do wnętrza cieczy - prostopadle do jej powierzchni. Siła ta przemieszcza cząsteczki znajdujące się w warstwie powierzchniowej cieczy do jej wnętrza dotąd, aż powierzchnia cieczy stanie się w danych warunkach p i T najmniejsza.
Dążenie cieczy do zmniejszania powierzchni swobodnej świadczy o pewnym podobieństwie warstwy powierzchniowej cieczy do napiętej, dążącej do kurczenia się błonki mydlanej.
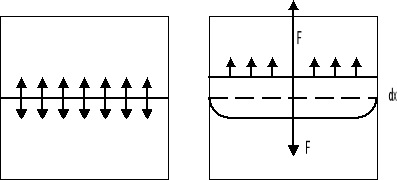
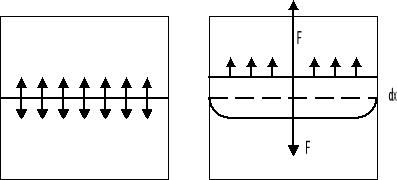
Na rysunku przedstawiona jest prostokątna, druciana ramka i dzieląca ja na dwie części ruchoma poprzeczka.
a) b)
W ramce rozciągnięta jest błonka mydlana ( wody mydlanej ). W przypadku a)- siły działające na poprzeczkę ze strony błonki w górę i w dół równoważą się wzajemnie i poprzeczka pozostaje w spoczynku. Jeżeli rozerwiemy błonkę dolną ( przypadek b) ), poprzeczka zaczyna przesuwać się w górę pod wpływem działającej siły ze strony błonki w górnej części ramki; dla jej zrównoważenia należy przyłożyć siłę Fr styczną do powierzchni i prostopadłą do długości L obwodu błonki.
Z doświadczeń wynika, że siła Fr ~L i ma wartość oraz kierunek takie same jak siła kurcząca F, nazwana siłą napięcia powierzchniowego.
Stosunek wartości siły F do długości L nazywamy napięciem powierzchniowym ![]()
lub współczynnikiem napięcia powierzchniowego.
![]()
W rozpatrywanym przykładzie błonka rozpięta na ramce ma dwie powierzchnie swobodne, a więc
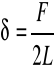
Jednostką miary napięcia powierzchniowego jest niuton na metr (N/m).
Obok powyższej ( mechanicznej ) definicji napięcia powierzchniowego jest wprowadzona równoważna jej definicja energetyczna. Praca jaką należy wykonać, aby powiększyć pole powierzchni cieczy o dS = 2Ldx wynosi dW = Fdx = 2![]()
Ldx = ![]()
dS i jest równa przyrostowi energii błonki o dE, czyli
![]()
![]()
Ta część energii wewnętrznej błonki, którą można zamienić na pracę, nosi nazwę energii swobodnej. Napięcie powierzchniowe jest więc liczbowo równe stosunkowi zmiany energii swobodnej błonki do zmiany pola jej powierzchni.
Dzięki działaniu sił napięcia powierzchniowego, każda zakrzywiona warstwa powierzchniowa wywiera na ciecz dodatkowe ciśnienie, oprócz ciśnienia doznawanego przez ciecz o powierzchni płaskiej. To dodatkowe ciśnienie jest dodatnie w przypadku powierzchni wypukłej i ujemne w przypadku powierzchni wklęsłej. Całkowita siła pionowa działająca na ciecz o powierzchni S wynosi:
![]()
gdzie ![]()
jest długością obwodu ograniczającego powierzchnię S.
Jeżeli powierzchnia cieczy jest wypukła to siła F ściska ciecz znajdującą się pod powierzchnią S, a więc wytwarza ciśnienie dodatnie; gdy powierzchnia cieczy jest wklęsła, to siła F wytwarza ciśnienie ujemne.
Biorąc pod uwagę, że ![]()
oraz ![]()
, można zapisać :
![]()
Wartość ciśnienia możemy obliczyć ze wzoru:
![]()
W przypadku zetknięcia się cieczy z ciałem stałym, należy uwzględnić zarówno siły, z jakimi oddziaływują na siebie cząsteczki cieczy / siły spójności - kohezji / jak i siły, które występują pomiędzy cząsteczkami cieczy i ciała stałego / siły przylegania - adhezji /.
Jeżeli siły spójności są większe od sił przylegania, to siła wypadkowa działająca na warstwę cieczy przylegającą do ciała stałego, jest skierowana w stronę cieczy /ciało stałe nie ulega zwilżaniu przez ciecz /. W stanie równowagi powierzchnia cieczy ustawia się prostopadle do siły wypadkowej, toteż w przedstawionych wyżej warunkach powstaje menisk wypukły. W przypadku gdy siły spójności są mniejsze od sił przylegania, wypadkowa siła skierowana jest w stronę ciała stałego, ciecz zwilża ścianki naczynia i wobec tego tworzy się menisk wklęsły.
W celu scharakteryzowania menisku wprowadza się pojęcie kąta granicznego ![]()
, który jest utworzony przez styczne do powierzchni cieczy i do powierzchni ciała stałego w punkcie ich zetknięcia. W zależności od rodzaju cieczy, może wystąpić zjawisko wznoszenia lub obniżania się poziomu cieczy w rurkach kapilarnych. Zjawisko to nosi nazwę włoskowatości.
Jeżeli ciecz zwilża materiał, z którego wykonana jest kapilara, wówczas w kapilarze tworzy ona menisk wklęsły. Dla kapilary o przekroju kołowym menisk uformuje się w przybliżeniu w kształcie powierzchni sferycznej. Pod wklęsłą powierzchnią cieczy wystąpi więc dodatkowe ciśnienie ujemne o wartości :
![]()
Ciecz w kapilarze podnosi się na taką wysokość h, przy której ciśnienie hydrostatyczne słupa cieczy zrównoważy ciśnienie p. Ciśnienie hydrostatyczne słupa cieczy o gęstości ![]()
jest równe
![]()
Warunek równowagi można więc zapisać następująco: ![]()
skąd ![]()
Gdy ciecz tworzy menisk wypukły, powstaje dodatnie ciśnienie dodatkowe i poziom cieczy w kapilarze obniża się. Na podstawie takiego eksperymentu i wzoru ![]()
można wyznaczyć
wartość współczynnika napięcia powierzchniowego
![]()
Promień krzywizny R występujący w powyższym wzorze nie daje się zmierzyć bezpośrednio, dlatego też należy go zastąpić promieniem kapilary r, a do wzoru należy zastosować zależność
![]()
Wprowadzając średnicę rurki d jako wielkość mierzoną bezpośrednio otrzymujemy:
![]()
(*)
Wykonanie ćwiczenia
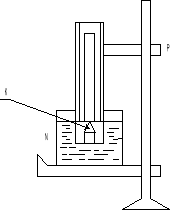
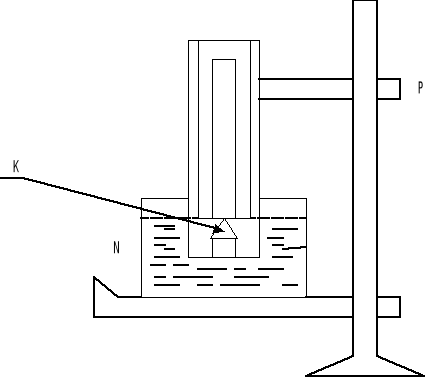
Pomiarów dokonujemy przy pomocy zestawu przedstawionego poniżej.
Otwartą obustronnie rurkę kapilarną umocowujemy na skali i wraz z nią wstawiamy ją do naczynia N z badaną cieczą. Za pomocą regulatora P zanurzamy skalę do dna, a następnie podnosimy ją tak, aby ostrze K dotykało od spodu powierzchni cieczy. Wysokość h cieczy odczytujemy jako różnicę położeń menisku cieczy i kolca. Następnie odłamujemy kawałeczek kapilary w miejscu gdzie znajdowała się ciecz i przy pomocy mikroskopu mierzymy jej średnicę wewnętrzną w działkach okularu. Znając wartość działki okularu, wyrażoną w metrach znajdujemy średnicę kapilary d.
Wyniki doświadczenia oraz obliczenia pozostałych wartości zamieszczone są w załączonej tabeli.
OBLICZENIA:
Wartość współczynnika napięcia powierzchniowego ![]()
na podstawie zależności (*) ;
![]()
Wartość średnią współczynnika napięcia powierzchniowego ![]()
;
![]()
Błędy bezwzględne poszczególnych pomiarów ;
![]()
![]()
Błędy względne procentowe poszczególnych pomiarów ;
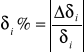
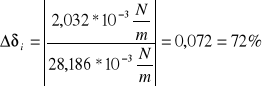
Błąd względny maksymalny możliwy do popełnienia obliczam metodą różniczkowania wzoru (*);
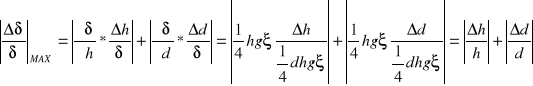
![]()
dokładność skali przyrządu pomiarowego
![]()
dokładność cechowania i odczytu na mikroskopie ![]()
dla cieczy MC-8 IV; (np. pomiar 4);
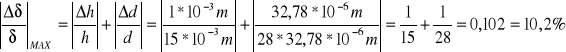
dla cieczy MC-8 II; (np. pomiar 1);
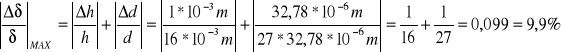
Wyszukiwarka
Podobne podstrony:
EM 3.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
J 4.1(2), Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania,
J 11.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
MC 3.2, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, L
06, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Labor
M 6 3, Politechnika Lubelska, Studia, Studia, fizyka
20'', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Lab
J 5 1, Politechnika Lubelska, Studia, Studia, fizyka
10, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Labor
14'''''''''', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozda
O 9 1, Politechnika Lubelska, Studia, Studia, fizyka
M-14.1P, Politechnika Lubelska, Studia, Studia, fizyka
el.cw4 - Obwody trójfazowe2, Politechnika Lubelska, Studia, Studia, Elektrotechnika - laboratorium,
Ćwiczenie 00, Politechnika Lubelska, Studia, Studia, fizyka
Tranzystorowe generatory napięć sinusoidalnych, Politechnika Lubelska, Studia, Elektrotechnika, ELEK
więcej podobnych podstron