2. Wstęp teoretyczny:
Ciecz charakteryzuje się bardzo ciasnym upakowaniem cząsteczek, dlatego też, każda cząstka znajduje się w zasięgu oddziaływania sił międzycząsteczkowych otaczających ją cząsteczek. Brak regularnego rozmieszczenia cząsteczek w cieczy, powoduje, że oddziaływanie danej cząsteczki z sąsiednimi cząsteczkami jest w każdym kierunku takie samo, czyli wypadkowa siła oddziaływania jest równa 0. Taka sytuacja ma miejsce tylko wtedy, kiedy cząsteczka znajduje się wewnątrz cieczy. Inaczej się dzieje, kiedy cząstka znajduje się na powierzchni cieczy. Sferyczna symetria oddziaływania cząsteczek zostaje zaburzona z powodu braku ciasno upakowanych cząsteczek nad powierzchnią cieczy. Dlatego na cząsteczkę znajdującą się bardzo blisko powierzchni działa wypadkowa sił międzycząsteczkowych różna od zera i skierowana do wnętrza cieczy. Na skutek tego powierzchnia cieczy zmniejsza się. Zatem przemieszczenie cząsteczek z wnętrza cieczy na jej powierzchnię jest związane z wykonaniem pracy przeciw tej sile. Wartość tej pracy jest proporcjonalna do przyrostu powierzchni, czyli: W=α∆S, gdzie α jest współczynnikiem napięcia powierzchniowego. Siły działające na każdy element cieczy w fazie powierzchniowej powodują ściskanie tej warstwy, jak również dociskanie jej do fazy objętościowej. Cieczy ścisnąć się nie da działając siłami skierowanymi jednym kierunku (ściskana warstwa będzie usiłowała się rozpłynąć, co byłoby równoznaczne ze zmniejszaniem się jej grubości). Jednak grubość warstwy powierzchniowej nie może się zmniejszyć, bo jest określona przez siły oddziaływania międzycząsteczkowego. Dlatego też, tendencja warstwy powierzchniowej do rozpływania się zostaje zrównoważona naprężeniem warstwy, czyli napięciem powierzchniowym cieczy.
Napięciem powierzchniowym σ danej cieczy na granicy z inną fazą nazywamy pracę potrzebną do izotermicznego zwiększenia powierzchni cieczy o jednostkę. Napięciem powierzchniowym σ nazywamy także siłę styczną do powierzchni cieczy, działającą na jednostkę długości obrzeża powierzchni cieczy.
W układzie SI wymiarem napięcia powierzchniowego σ jest J/m2 lub N/m.
Biorąc pod uwagę ramkę z poprzeczką, na której jest rozpięta błonka z cieczy (mydlanej) i wyrażając odpowiednio pracę i przyrost powierzchni o ∆x znajdujemy łatwo, że α=F/l [N/m], gdzie l jest długością krawędzi powierzchni cieczy. Wnioskujemy, że współczynnik napięcia powierzchniowego wyraża siłę przypadającą na jednostkę długości krawędzi powierzchni cieczy. Jak również wyraża pracę przypadającą na jednostkową zmianę powierzchni cieczy α=W/∆S [J/m2]. α zależy od rodzaju cieczy np. mydła, detergenty, lipidy zmniejszają napięcie powierzchniowe, natomiast sole, kwasy, i inne substancje nieorganiczne zwiększają napięcie powierzchniowe.
Na granicy cieczy oraz gazu lub ciała stałego obserwuje się zakrzywienie powierzchni cieczy, zwane meniskiem. Menisk jest wynikiem rozkładu sił, które działają na cząsteczki cieczy znajdujące się w pobliżu granic trzech faz: cieczy, gazu i ciała stałego. Siłami kohezji nazywamy siły działające między cząsteczkami tego samego ciała. Siłą adhezji nazywamy siłę działającą między cząsteczkami różnych ciał.
Dzięki istnieniu napięcia powierzchniowego pod zakrzywiona powierzchnią cieczy działa dodatkowe ciśnienie. Według Laplace'a to dodatkowe ciśnienie określa wzór:
p= σ (1/R1 + 1/R2),
gdzie: R1 i R2 - promienie krzywizny prostopadłych względem siebie przekrojów normalnych, dla których promienie krzywizny przyjmują wartości ekstremalne. Promienie R1 i R2 uważamy za dodatnie, gdy środki krzywizn przekrojów normalnych znajdują się po stronie cieczy, za ujemne zaś, gdy są po stronie przeciwnej.
W związku z tym dla menisku wklęsłego p<0, a dla menisku wypukłego p>0. Dodatkowe ciśnienie jest zawsze skierowane w kierunku środka krzywizny menisku. Gdy R1=R2=R (wycinek powierzchni kuli), wtedy p = 2σ / R. Takie jest dodatkowe ciśnienie wewnątrz pęcherzyka gazu o promieniu R, gdy znajduje się on tuż pod powierzchnią cieczy. W cienkich kapilarach dodatkowe ciśnienie pod zakrzywioną powierzchnią powoduje wznoszenie się cieczy, gdy menisk jest wklęsły (zwilżanie) i opadanie cieczy gdy menisk jest wypukły (brak zwilżania).
3. Zasady pomiarów:
4. Wyniki pomiarów:
Pomiary zostały wykonane przy temperaturze pokojowej równej:
T = 23,0 0,1C
metoda odrywania:
- woda destylowana + płytka miedziana:
Lp. |
F |
|
[mN] |
1. |
2 |
2. |
2 |
3. |
2 |
4. |
2 |
- woda destylowana + płytka miedziana po umyciu:
Lp. |
F |
|
[mN] |
1. |
2,0 |
2. |
2,0 |
3. |
2,2 |
4. |
2,2 |
Wymiary blaszki miedzianej:
Lp. |
Szerokość d |
Wysokość h |
Grubość |
|
[mm] |
[mm] |
[mm] |
1. |
26 |
21,7 |
0,8 |
2. |
26,1 |
22,0 |
0,5 |
3. |
25,2 |
21,8 |
0,7 |
∆suwmiarki: 0,05 [mm]
Płytkę ważymy 3 razy po czym obliczamy wartość średnią:
- woda destylowana + płytka stalowa:
Lp. |
F |
|
[mN] |
1. |
2,45 |
2. |
2,35 |
3. |
2,50 |
4. |
2,45 |
- woda destylowana + płytka stalowa po umyciu:
Lp. |
F |
|
[mN] |
1. |
2,30 |
2. |
2,40 |
3. |
2,25 |
4. |
2,30 |
Wymiary blaszki stalowej:
Lp. |
Szerokość d |
Wysokość h |
Grubość |
|
[mm] |
[mm] |
[mm] |
1. |
25,8 |
21,9 |
0,75 |
2. |
25,8 |
21,8 |
0,5 |
3. |
25,8 |
22,0 |
0,7 |
pomiar napięcia powierzchniowego metodą stalagmometru:
Korzystałyśmy z wagi elektronicznej BE5000
Błąd ∆wagi= 0,1g
Wykonywałyśmy po trzy pomiary:
Masa pustego naczynia:
- 19,6g
- 19,6g
- 19,6g
Masa naczynia z 50 kroplami wody:
- 23,4g
- 23,3g
- 23,5g
Średnica zewnętrzna kapilary:
- 0,50 cm
- 0,55 cm
- 0,54 cm
∆xsuwmiarki: 0,05 cm
Wyniki obliczeń:
b) Metoda stalagmometru:
Lp. |
Masa pustego naczynia |
Masa naczynia z wodą |
Średnica kapilary 2r |
promień kapilary |
|
[g] |
[g] |
[mm] |
[mm] |
1. |
19,6 |
23,4 |
5 |
2,5 |
2. |
19,6 |
23,3 |
5,5 |
2,75 |
3. |
19,6 |
23,5 |
5,4 |
2,7 |
Wartość średnia |
19,6 |
23,4 |
5,3 |
2,65 |
|
mpn |
∆mpn |
mnc |
∆mnzc |
mk |
∆mk |
R |
|
∆R |
|
[kg] |
[kg] |
[kg] |
[kg] |
[kg] |
[kg] |
[m] |
|
[m] |
|
0,0196 |
0 |
0,0234 |
5,7735E-05 |
7,6E-05 |
0,000004 |
0,0025 |
|
7,63763E-05 |
|
0,0196 |
0 |
0,0233 |
|
0,000074 |
0,000004 |
0,00275 |
|
|
|
0,0196 |
0 |
0,0235 |
|
7,8E-05 |
0,000004 |
0,0027 |
|
|
wartość średnia |
0,0196 |
0 |
0,0234 |
|
7,6E-05 |
0,000004 |
0,00265 |
|
|
Lp. |
g |
t |
∆t |
ρ |
U |
∆U |
K |
∆K |
σ |
∆σ |
∆σ/σ |
|
[m/s2] |
oC |
oC |
|
|
|
|
|
[N/m] |
[N/m] |
[%] |
|
9,81 |
23 |
0,1 |
0,00001 |
3,040 |
0,160 |
0,26068 |
0,01 |
0,077741032 |
0,007082 |
9,109706 |
|
|
|
|
|
2,691 |
0,145 |
0,26198 |
0,01 |
0,069157004 |
0,006385 |
9,232896 |
|
|
|
|
|
2,889 |
0,148 |
0,2611 |
0,01 |
0,07399574 |
0,006636 |
8,968565 |
Wartość średnia |
|
|
|
|
2,868 |
0,151 |
|
|
0,073631259 |
0,006701 |
|
∆g= 10-3[m/s2] (przyjmuję na podstawie skryptu)
UWAGI DLA MOJEJ EWELINKI :
Mpn- masa pustego naczynia
Mnc- masa naczynia z cieczą
Mk- masa kropli
R- promień kapilary
(weż ładnie zrób te oznaczenia + do tego przykładowe obliczenia, ja Ci wszystkie wzory podam poniżej ok.? Jakbyś miala problem to wal śmiało)
∆mpn |
|
∆mnzc |
|
|
|
∆R |
Te delty liczyłam z odcylenia standardowego:
- Obliczanie odchylenia standardowego
- Obliczanie średniej arytmetycznej:
- Obliczanie masy kropli:
![]()
- Obliczanie błędu masy kropli za pomocą różniczki zwyczajnej:
- błąd ważenia na wadze laboratoryjnej wynosi Δm = 1⋅10-4, z czego błąd pojedynczej kropli obliczamy za pomocą różniczki zupełnej:
![]()
(MOJA UWAGA: TE DELTY SĄ RÓWNE Δm = 1⋅10-4 WIĘC W PRZYKŁADOWYCH OBLICZENIACH DODAJESZ TE DWIE DELTY M I DZIELISZ PRZEZ 50 I WYCHODZI Ci wynik w tabelce)
- Obliczanie promienia kapilary:
![]()
- Obliczanie U
![]()
- Obliczanie wartości średniej dla U (wartość złożona):
![]()
- ΔU obliczamy posługując się metodą różniczki logarytmicznej:
UWAGA DLA EWELINKI: podstawiałam tylko o tego ostatniego wzoru żeby wyliczyć delte U
- ΔK został określony na podstawie wartości błędu ΔU oraz tablicy ze współczynnikami K.
- błąd wartości napięcia powierzchniowego obliczamy za pomocą różniczki logarytmicznej:
I TAK JAK OSTATNIO PODSTAWIASZ TYLKO DO TEGO OSTATNIEGO WZORU
M- MASA KROPLI
g- przyspieszenie ziemskie
metoda odrywania:
blaszka mosiężna/ miedziana (pierwsza tabelka)
masa plytki |
∆m |
Q |
∆Q |
F |
∆F |
l |
∆l |
d |
∆d |
σ |
∆σ |
∆σ/σ |
[kg] |
[kg] |
[N] |
[N] |
[N] |
[10^-3 N] |
[m] |
[m] |
[m] |
[m] |
|
|
[%] |
0,000290 |
0,000204826 |
0,002844 |
0,002008942 |
0,002 |
0,1 |
0,026 |
0,000285 |
0,0008 |
8,82E-05 |
0,015745 |
0,005579 |
35,43441 |
0,000290 |
|
0,002844 |
0,002008942 |
0,002 |
0,1 |
0,0261 |
|
0,0005 |
|
0,015863 |
|
|
0,000289 |
|
0,002834 |
0,002008941 |
0,0022 |
0,1 |
0,0252 |
|
0,0007 |
|
0,012242 |
|
|
|
|
|
|
0,0022 |
0,1 |
|
|
|
|
|
|
|
0,00029 |
|
0,002841 |
0,002008942 |
0,0021 |
|
0,025766667 |
|
0,000667 |
|
|
|
|
Druga tabelka dla płytki mosiężnej
Lp |
masa plytki |
∆m |
Q |
∆Q |
F |
∆F |
l |
∆l |
d |
∆d |
σ |
∆σ |
∆σ/σ |
|
[kg] |
[kg] |
[N] |
[N] |
[N] |
[10^-3 N] |
[m] |
[m] |
[m] |
[m] |
|
|
[%] |
|
0,000290 |
0,000204826 |
0,002844 |
0,002008942 |
0,002 |
0,1 |
0,026 |
0,000285 |
0,0008 |
8,82E-05 |
0,015745 |
0,005592 |
35,51839 |
|
0,000290 |
|
0,002844 |
0,002008942 |
0,002 |
0,1 |
0,0261 |
|
0,0005 |
|
0,015863 |
|
|
|
0,000289 |
|
0,002834 |
0,002008941 |
0,002 |
0,1 |
0,0252 |
|
0,0007 |
|
0,016103 |
|
|
|
|
|
|
|
0,002 |
0,1 |
|
|
|
|
|
|
|
wartość średnia: |
0,00029 |
|
0,002841 |
0,002008942 |
0,002 |
|
0,025766667 |
|
0,000667 |
|
|
|
|
Pierwsza tabelka dla płytki stalowej:
|
masa plytki |
∆m |
Q |
∆Q |
F |
∆F |
l |
∆l |
d |
∆d |
σ |
∆σ |
∆σ/σ |
|
[kg] |
[kg] |
[N] |
[N] |
[N] |
[N] |
[m] |
[m] |
[m] |
[m] |
[N/m] |
[N/m] |
[%] |
|
0,000310 |
3,33333E-06 |
0,00304 |
3,29988E-05 |
0,00245 |
0,1 |
0,026 |
0,0002848 |
0,0008 |
8,82E-05 |
0,011009 |
0,005899 |
53,58136 |
|
0,000320 |
|
0,003138 |
3,30088E-05 |
0,00235 |
0,1 |
0,0261 |
|
0,0005 |
|
0,014814 |
|
|
|
0,000310 |
|
0,00304 |
3,29988E-05 |
0,0025 |
0,1 |
0,0252 |
|
0,0007 |
|
0,010426 |
|
|
|
|
|
|
|
0,00245 |
0,1 |
|
|
|
|
|
|
|
wartość średnia |
0,000313 |
|
0,003073 |
3,30022E-05 |
0,002438 |
|
0,025766667 |
|
0,000667 |
|
|
|
|
Druga tabelka dla płytki stalowej:
|
masa plytki |
∆m |
Q |
∆Q |
F |
∆F |
l |
∆l |
d |
∆d |
σ |
∆σ |
∆σ/σ |
|
[kg] |
[kg] |
[N] |
[N] |
[N] |
[N] |
[m] |
[m] |
[m] |
[m] |
[N/m] |
[N/m] |
[%] |
|
0,000310 |
3,33333E-06 |
0,00304 |
3,29988E-05 |
0,0023 |
0,1 |
0,026 |
0,0002848 |
0,0008 |
8,82E-05 |
0,013807 |
0,005907 |
42,78131 |
|
0,000320 |
|
0,003138 |
3,30088E-05 |
0,0024 |
0,1 |
0,0261 |
|
0,0005 |
|
0,013875 |
|
|
|
0,000310 |
|
0,00304 |
3,29988E-05 |
0,0025 |
0,1 |
0,0252 |
|
0,0007 |
|
0,010426 |
|
|
|
|
|
|
|
0,0023 |
0,1 |
|
|
|
|
|
|
|
wartość średnia |
0,000313 |
|
0,003073 |
3,30022E-05 |
0,002375 |
|
0,025766667 |
|
0,000667 |
|
|
|
|
Wzory które wykorzystałam:
- deltę m, l, d- z odchylenia standardowego:
Średnie wartości z średniej arytmetycznej:
- Obliczenia Q:
![]()
g- przyspieszenie ziemskie =9,80665[m/s2] |
-Obliczenie ∆Q z różniczki zupełnej:
![]()
∆g= 0,001
- Obliczenie napięcia powierzchniowego:
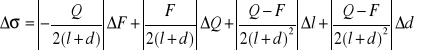
I w tym wzorze podtsawiasz sobie srednie wartości F, Q, l, d, delty Q,F,l i d ;)
Wyszukiwarka
Podobne podstrony:
Fifyka komputerowa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Elektronika 03, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
fiele25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
Pomia napięcia powierzchniowego, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, spr
fiele15, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
lista4elektronika(1), Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Sprawozdanie 81, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
Sprawozdanie nr12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fi
Sprawozdanie nr43 fizyka, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdan
Sprawozdanie 12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
LABORATORIUM, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Sprawozdanie 57c, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fiz
pp25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Labora
zas nieoznaczonosci, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Fizyka II - Popko, fiz
POCHODNA FUNKCJI, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
76, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, fiza lab
LAB51~1, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, fiz
więcej podobnych podstron