1. Ciśnienia w poruszającym się płynie

W poruszającym się strumieniu płynu (gaz lub ciecz), wyróżniamy ciśnienie statyczne, ciśnienie dynamiczne i ciśnienie całkowite. Ciśnienie statyczne jest to ciśnienie wskazywane przez przyrząd poruszający się w strumieniu płynu z taką samą prędkością i w tym samym kierunku, w którym porusza się płyn tak, aby prędkość względna przyrządu i płynu była równa zeru. Jeżeli płyn nie porusza się, tj. pozostaje w stanie spoczynku ciśnieniem, jakie w nim panuje, jest ciśnienie statyczne. Ciśnienie dynamiczne występuje tylko podczas ruchu płynu.

Jest ono nierozerwalnie związane z prędkością przepływu płynu. Wielkość ciśnienia dynamicznego wyraża zależność:

(1)

Ciśnienie całkowite (spiętrzenia) p_c jest sumą ciśnienia statycznego p_s i ciśnienia dynamicznego p_d:

(2)

W płynie pozostającym w spoczynku ciśnienie całkowite jest równe ciśnieniu statycznemu, zatem, jeżeli v = 0, to p_c = p_s.

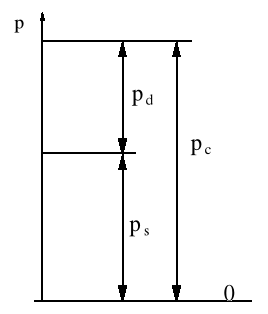
Rys. 1. Graficzna ilustracja zależności między ciśnieniami w płynie

2. Metody pomiaru ciśnień

Do pomiaru ciśnienia statycznego i dynamicznego stosuje się typowe manometry cieczowe różnicowe. O samym pomiarze decyduje sposób podłączenia przyrządu pomiarowego. Podczas pomiarów stosuje się króćce lub specjalne rurki pomiarowe podłączone do manometru. W celu wyeliminowania wpływu prędkości płynu stosuje się króćce pomiarowe, ustawione w ten sposób, że wektor prędkości przepływu jest styczny do płaszczyzny wlotowej otworu impulsowego. Zasadę pomiaru ciśnienia statycznego przedstawiono na rys. 2.

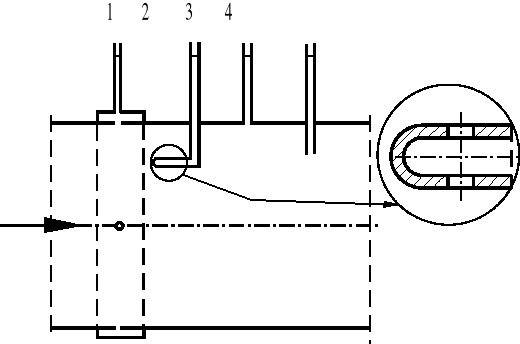
Rys.2. Przyrządy do pomiaru ciśnienia statycznego. 1 - pierścień impulsowy, 2 - rurka z otworami impulsowymi, 3 - piezometr, 4 - króciec pomiarowy

Pomiar ciśnienia dynamicznego polega na oddzielnym pomiarze ciśnienia statycznego i ciśnienia całkowitego oraz na wykorzystaniu manometru różnicowego, który wskazuje różnicę między ciśnieniem całkowitym i statycznym, a więc ciśnienie dynamiczne. Zasadę pomiaru ciśnienia dynamicznego przedstawiono na rys. 3. Do pomiaru ciśnienia statycznego zastosowano piezometr, natomiast do pomiaru ciśnienia całkowitego rurkę spiętrzeniową zwaną rurką Pitota. Rurka ta jest wygięta pod kątem prostym i ustawiona otwartym końcem pod prąd tak, aby powierzchnia otworu impulsowego była prostopadła do kierunku przepływu. Z chwilą gdy rurka wypełni się cieczą do wysokości H, ciecz przestaje do niej napływać i na powierzchni przekroju wlotowego ciecz zostaje wyhamowana do prędkości v=0. Powierzchnię, na której płyn zostaje wyhamowany do prędkości v=0, nazywamy powierzchnią spiętrzenia. Rurka Pitota mierzy ciśnienie całkowite panujące na tej powierzchni, które jest sumą ciśnienia statycznego i dynamicznego. Podłączenie manometru różnicowego do układu rurka Pitota - piezometr umożliwia bezpośredni pomiar ciśnienia dynamicznego (rys.3). Wykorzystuje się przy tym następującą zależność:

(3)

Wykorzystując fakt, że ciśnienie dynamiczne jest zależne od prędkości przepływu płynu, można w sposób pośredni zmierzyć prędkość przepływu. Ze wzorów (1) i (3) wynika następująca zależność:

(4)

skąd

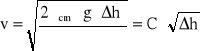
(5)

gdzie: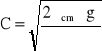
(6)

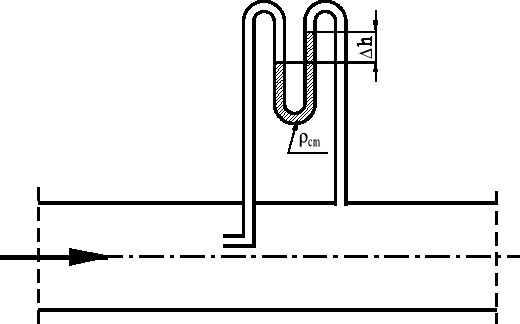
Rys.3 Schemat układu do pomiaru ciśnienia dynamicznego

Pomiar ciśnienia dynamicznego umożliwia zatem obliczenie odpowiadającej temu ciśnieniu prędkości przepływu. Możliwe jest również odpowiednie wyskalowanie manometru różnicowego w jednostkach prędkości, np. w m/s.

Do bezpośredniego pomiaru ciśnienia dynamicznego służy tzw. rurka Prandtla. Aby łatwiej zrozumieć zasadę jej działania, należy zapoznać się ze zjawiskami występującymi podczas opływu płynu wokół przeszkody (rys.4).

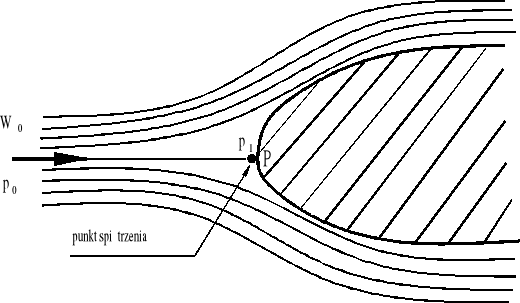
Rys.4 Opływ płynu wokół przeszkody

Jeżeli na drodze płynu poruszającego się ze stałą prędkością v₀, znajdzie się przeszkoda w postaci ciała zanurzonego, wówczas bezpośrednio przed nią występuje zjawisko spiętrzenia przepływu. W punkcie P, zwanym punktem spiętrzenia (rys.4), następuje całkowite zahamowanie przepływu (prędkość przepływu w tym punkcie jest równa zeru). Rozpatrzmy przepływ wzdłuż linii prądu (zaznaczonej na rysunku strzałką) biegnącej do tego punktu. W znacznej odległości przed przeszkodą prędkość przepływu jest równa v_0.

Ciśnienie panujące w punkcie spiętrzenia oznaczono przez p₁, a ciśnienie panujące w miejscu niezakłóconego przepływu - w znacznej odległości od przeszkody i na tej samej wysokości, na której znajduje się punkt spiętrzenia oznaczono przez p₀. Wówczas dla rozpatrywanej poziomej linii prądu równanie Bernoulliego przyjmie postać:

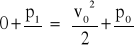
(7)

stąd ciśnienie w punkcie spiętrzenia:

(8)

Zatem przyrost ciśnienia w punkcie spiętrzenia wyniesie:

(9)

Obliczona wielkość różnicy ciśnień jest więc ciśnieniem dynamicznym. Jeżeli w punkcie spiętrzenia rozpatrywanej przeszkody wywiercony zostanie niewielki otwór, to wówczas wewnątrz tego otworu będzie panowało ciśnienie spiętrzenia p₁. Ciśnienie to może być doprowadzone do przyrządu pomiarowego.

Rurka Prandtla zbudowana jest z dwóch współosiowo umieszczonych rurek metalowych. Część rurki skierowana pod prąd w stosunku do kierunku przepływu płynu zakończona jest półkulą, w osi której wywiercony jest mały otwór. Na półkuli tej występuje zjawisko spiętrzenia; poprzez otwór i rurkę doprowadzane jest do manometru ciśnienie spiętrzenia. Pomiar ciśnienia statycznego realizowany jest za pomocą otworków umieszczonych symetrycznie na obwodzie zewnętrznej rurki. Przyjmuje się, że w odległości równej trzem średnicom rurki zewnętrznej (licząc od jej początku) ciśnienie statyczne na powierzchni rurki osiąga wartość ciśnienia statycznego odpowiadającego przepływowi niezakłóconemu.

Konstrukcja rurki umożliwia oddzielny pomiar ciśnienia całkowitego, ciśnienia statycznego oraz dynamicznego w zależności od sposobu połączenia jej z mikromanometrem cieczowym (rys. 5). Stosuje się go do pomiaru małych ciśnień do 160 mm H₂O. Składa się on ze zbiornika pomiarowego (1) zamocowanego na podstawce i szklanej rurki (2) umieszczonej na ruchomym ramieniu, składającym się m.in. z kątownika (3). Wartość różnicy ciśnień Δp oblicza się ze wzoru:

,[ N/m² ] (10)

gdzie:
- przełożenie manometru,

α− kąt nachylenia rurki pomiarowej, rad

f − pole powierzchni przekroju rurki, m²

F − pole powierzchni przekroju zbiornika, m²

Ponieważ wartość stosunku
jest pomijalnie mała w porównaniu z wartością sinα, powszechnie przyjmuje się we wzorze (10), że n = sinα.

Obecnie mikromanometry cieczowe zostały zastąpione nowoczesnymi elektronicznymi mikromanometrami różnicowymi.

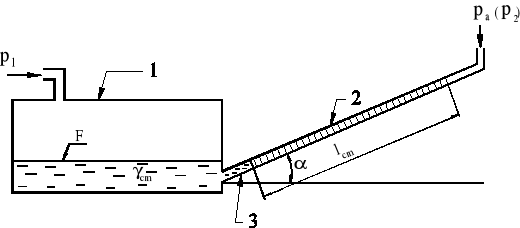
Rys. 5. Schemat mikromanometru cieczowego

Na rys. 6. pokazano zasadę pomiaru ciśnienia dynamicznego za pomocą rurki Prandtla. Rozpatrzmy strugę leżącą w osi tej rurki i obierzmy na niej dwa przekroje, z których jeden wypada w punkcie spiętrzenia, a drugi leży w obszarze przepływu niezakłóconego (przyjmuje się, że jest on oddalony od punktu spiętrzenia co najmniej o trzy średnice rurki)

Zakładając, że przepływający płyn jest nieściśliwy i przepływ jest ustalony równanie Bernouliego dla przekrojów 1-1 i 2-2 przyjmie następującą postać:

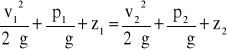
(11)

Przy poziomym usytuowaniu rurki z₂ = z₁. Ponadto w punkcie spiętrzenia mamy v = 0 oraz p₁ = p_c..

W płaszczyźnie otworków w zewnętrznej części rurki Prandtla (przekrój 2 - 2) mamy p₂= p_s oraz
v₂ = v.

Po podstawieniu powyższych wartości do równania (11) otrzymuje się:

(12)

skąd:

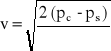
(13)

Jeżeli rurkę podłączymy do manometru różnicowego, to zmierzymy różnicę ciśnień całkowitego i statycznego. Znając różnicę ciśnień i korzystając ze wzoru (13) można obliczy* prędkość przepływu v.

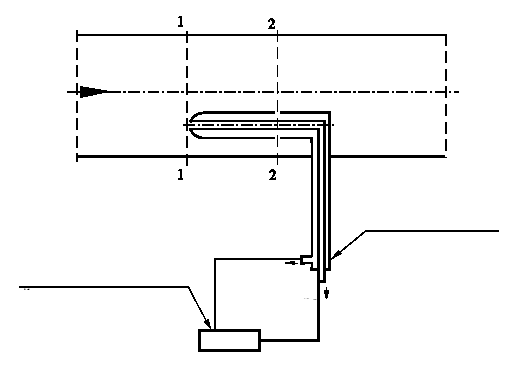
Rys. 6. Zasada pomiaru ciśnień rurką Prandtla

3. Pomiar strumienia objętości metodą zwężkową.

Prześledźmy ustalony ruch płynu nielepkiego i nieściśliwego w poziomej rurze, w której pewien odcinek zastąpiono przewężeniem - zwężką (rys.7). Równanie Bernoulliego dla przekrojów 1. i 2. ma postać :

(14)

Z równania ciągłości wiadomo, że:

v₁=v₂(d/D)²=β² v₂ (15)

Stosunek średnicy otworu (gardzieli) zwężki (d) do średnicy wewnętrznej rurociągu(D) nazywamy przewężeniem β=d/D.

Rys.7. Odbiór ciśnień w zwężce pomiarowej

Po rozwiązaniu układu równań względem v₂, otrzymamy

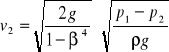
(16)

a zatem:

miarą średniej prędkości przepływu przez zwężkę jest spadek ciśnienia (Δp =p₁- p₂) między jej przekrojami mierniczymi, zwany ciśnieniem różnicowym.

W przypadku pomiaru ciśnienia różnicowego za pomocą manometru różnicowego zależność (16) przyjmuje postać

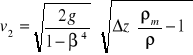
(17)

Na podstawie wartości prędkości średniej obliczamy strumień objętości przy zna­nych wartościach bezwzględnych ciśnień statycznych w obu przekrojach (lub ich róż­nicy)

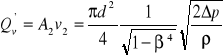
(18)

Lub strumień masy

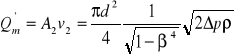
(19)

Zależności te nie uwzględniają zjawisk występujących podczas przepływu płynów lepkich, konieczne jest zatem wprowadzenie współczynnika korygującego C, zwanego współczynnikiem przepływu, charakteryzującego zależność między rzeczywistym a teoretycznym strumieniem objętości lub masy. Współczynnik ten zależy jedynie od liczby Reynoldsa C = C(Re_D) dla danego typu zwężki pomiarowej. Re_D = vD/v.

Jeśli ponadto płyn jest ściśliwy, to trzeba wprowadzić następny współczynnik ε₁ (wyznaczony doświadczalnie i podany w normie), zwany liczbą ekspansji. Liczba ta (odniesiona do przekroju przepływowego przed zwężką) uwzględnia zmianę gęstości przepływającego płynu wskutek spadku ciśnienia w przewężeniu. Liczba ekspansji nie zależy od liczby Reynoldsa, a dla danego przewężenia zwężki pomiarowej zależy wyłącznie od ilorazu ciśnienia różnicowego i ciśnienia absolutnego przed zwężką Δp/p) oraz od wykładnika izentropy danego gazu. Dla praktycznie nieściśliwych cie­czy ε₁ = 1; dla płynów ściśliwych ε₁ < 1.

Ostatecznie strumień objętości płynów rzeczywistych określa wzór

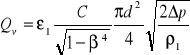
(20)

Gdzie:

Δp≡ Δp₁₂ - jest ciśnieniem różnicowym pomierzonym przed i za zwężką w miej­scach ustalonych odpowiednią normą (PN-93/M-53950/01)-rys.7,

p₁ - gęstość płynu w przekroju mierniczym przed zwężką (dla cieczy ρ₁= ρ₂= ρ),

ε₁ - liczba ekspansji odniesiona do warunków przed zwężką.

Zależność Q_v=Q_v(Δp) określona wzorem (20) jest zwana charakterystyką zwęż­ki. Na rysunkach 8 i 9 przedstawiono schematy dwóch rodzajów zwężek pomia­rowych: kryzy pomiarowej i klasycznej zwężki Venturiego oraz pokazano rozkład ciśnienia wzdłuż osi przewodu (linią przerywaną) i w pobliżu ścian (linią ciągłą).

Rys. 8. Rozkład ciśnienia podczas przepływu przez rurę z kryzą pomiarową.

Przepływowi płynu rzeczywistego przez zwężkę towarzyszy strata energii. Wartość tej straty zależy przede wszystkim od przewężenia zwężki (β) oraz od sposobu dławie­nia strugi przepływającego czynnika, czyli od rodzaju zwężki. Najmniejszymi stratami energii charakteryzuje się zwężka Venturiego, w której nie ma gwałtownych zmian pola przekroju przepływowego. Największe straty wywołuje wbudowanie kryzy.

Rys. 9. Rozkład ciśnienia wzdłuż klasycznej zwężki Venturiego.

Na rysunku 10 podano orientacyjne zależności względnej trwałej straty ciśnienia ξ (iloraz straty ciśnienia Δω i ciśnienia różnicowego Δp) od przewężenia β przedsta­wionych typów zwężek.

Rys. 10. Zależność względnej trwałej straty ciśnienia od przewężenia dla kryzy i zwężki Venturiego

Literatura:

Krystyna Jeżowiecka - Kabsch, Henryk Szewczyk, Mechanika płynów- Oficyna Wydawnicza Politechniki Wrocławskiej -2001.

Jerzy Bukowski, Mechanika płynów- PWN, Warszawa 1959.

1

---