BADANIE ANHARMONICZNOŚCI DRGAŃ WAHADŁA MATEMATYCZNEGO WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO

I. Wstęp

Wahadłem matematycznym nazywamy punkt materialny który porusza się po okręgu koła w polu grawitacyjnym.

By wahadło było uznane za wahadło matematyczne proste musi spełniać kilka założeń:

• drganie wykonuje punkt materialny o masie „m” i zawieszony na nici długości „l”

• nić jest nie rozciągliwa i nieważka

• punkt zaczepienia jest stały

• na wahadło działa tylko siła ciężkości oraz siła naciągu nici

Równanie ruchu wahadła możemy zapisać w postaci

podstawiając

rozwiązując to równanie otrzymamy wzór na okres wahadła matematycznego.

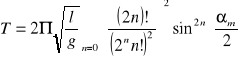
Powyższy wzór możemy zapasać pisząc kilka pierwszych wyrazów ciągu.

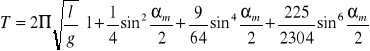
W praktyce ciężko jest zmierzyć długość l wahadła. By z zminimalizować błąd wynikający z niedokładnego wyznaczenia długości l stosuje się tzw. wahadło różnicowe. W wahadle różnicowym zmieniamy długość wahadła d = (l₀+ l_i .)W tej sytuacji można napisać

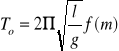
oraz

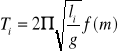
podnosząc obydwie strony do kwadratu otrzymamy

d = (l₀₊l_i)

gdzie
=

korzystając z powyższego wzoru możemy wyznaczyć przyspieszenie ziemskie g.

II. Wykonanie ćwiczenia

Zestaw przyrządów:

• statyw na którym jest zawieszone wahadło

• miernik czasu o dokładność 0,001 sekundy

• miarko o dokładność 0,002 m

• wahadło

• kątomierz o dokładności 1^o

Odchylamy wahadło o kąt wahadło i marzymy polowe okres drgań wahadła następnie jeszcze raz odchylamy wahadło z pozycji równowagi i mierzymy następną polówkę okresu, później zmieniamy długość l₀ wahadła o 3 centymetry i powtarzamy pomiar postępujemy aż do uzyskania 21 serii pomiarowych. Wyniki przedstawia poniższa tabela.

Lp.	d (m)	T P [s]	T L [s]	Suma [s]	T0^2 + Ti^2
1	0	0,4768	0,4781	0,9549
2	0,03	0,5040	0,5033	1,0073	1,9622
3	0,06	0,5410	0,5442	1,0852	2,0925
4	0,09	0,5691	0,5681	1,1372	2,2224
5	0,12	0,5947	0,5933	1,1880	2,3252
6	0,15	0,6155	0,6284	1,2439	2,4319
7	0,18	0,6501	0,6555	1,3056	2,5495
8	0,21	0,6757	0,6753	1,3510	2,6566
9	0,24	0,6956	0,6965	1,3921	2,7431
10	0,27	0,7165	0,7158	1,4323	2,8244
11	0,30	0,7342	0,7311	1,4653	2,8976
12	0,33	0,7545	0,7539	1,5084	2,9737
13	0,36	0,7806	0,7803	1,5609	3,0693
14	0,39	0,7841	0,7851	1,5692	3,1301
15	0,42	0,8073	0,8071	1,6144	3,1836
16	0,45	0,8314	0,8289	1,6603	3,2747
17	0,48	0,8534	0,8531	1,7065	3,3668
18	0,51	0,8572	0,8500	1,7072	3,4137
19	0,54	0,8704	0,8705	1,7409	3,4481
20	0,57	0,8975	0,8968	1,7943	3,5352
21	0,60	0,9098	0,9083	1,8181	3,6124

Następnie zmierzyliśmy zależność amplitudy drgań od kąta wychylenia wahadła. W tym celu ustawiamy stałą długość wahadła i zmieniamy kąt o jaki wychylamy wahadło. Wynik przedstawia poniższa tabela

		Strona prawa [s]					Średnia	Strona lewa[s]					Średnia	Suma[s]					Średnia
lp	kąt [^o]	1	2	3	4	5		1	2	3	4	5		1	2	3	4	5
1	5	0,44	0,438	0,4375	0,4387		0,4386	0,439	0,439	0,391	0,389		0,4145	0,879	0,877	0,8285	0,8277		0,8531
2	10	0,4127	0,4196	0,4182	0,4173	0,4163	0,4168	0,4135	0,4182	0,4155	0,416	0,4145	0,4155	0,8262	0,8378	0,8337	0,8333	0,8308	0,8324
3	15	0,423	0,4221	0,4254	0,4246	0,4279	0,4246	0,4238	0,4229	0,4248	0,48	0,4257	0,4354	0,8468	0,845	0,8502	0,9046	0,8536	0,8600
4	20	0,4276	0,4287	0,4296	0,4309	0,4313	0,4296	0,4267	0,428	0,4285	0,428	0,4291	0,4281	0,8543	0,8567	0,8581	0,8589	0,8604	0,8577
5	25	0,4336	0,4328	0,4324	0,4328	0,4352	0,4334	0,4325	0,4318	0,4313	0,4318	0,4346	0,4324	0,8661	0,8646	0,8637	0,8646	0,8698	0,8658
6	30	0,4362	0,4372	0,4367	0,4359	0,4352	0,4362	0,4361	0,4353	0,4358	0,4357	0,4342	0,4354	0,8723	0,8725	0,8725	0,8716	0,8694	0,8717
7	35	0,4381	0,4385	0,4396	0,4394	0,4399	0,4391	0,4396	0,4395	0,4396	0,4393	0,4391	0,4394	0,8777	0,878	0,8792	0,8787	0,879	0,8785
8	40	0,4439	0,4432	0,4449	0,4454	0,4459	0,4447	0,4428	0,4431	0,4493	0,4449	0,4448	0,4450	0,8867	0,8863	0,8942	0,8903	0,8907	0,8896
9	45	0,4481	0,4479	0,4479	0,4475	0,4473	0,4477	0,4479	0,4471	0,4485	0,4482	0,4481	0,4480	0,896	0,895	0,8964	0,8957	0,8954	0,8957
10	50	0,4514	0,4539	0,4523	0,4549	0,4544	0,4534	0,4507	0,4521	0,4515	0,4538	0,4539	0,4524	0,9021	0,906	0,9038	0,9087	0,9083	0,9058
11	55	0,4566	0,4585	0,4563	0,4584	0,4581	0,4576	0,4561	0,4562	0,4554	0,4567	0,457	0,4563	0,9127	0,9147	0,9117	0,9151	0,9151	0,9139
12	60	0,462	0,462	0,4628	0,4625	0,4623	0,4623	0,4612	0,4623	0,4618	0,4624	0,4621	0,4620	0,9232	0,9243	0,9246	0,9249	0,9244	0,9243
13	65	0,4621	0,4678	0,4659	0,4671	0,466	0,4658	0,4631	0,4643	0,4659	0,4664	0,4657	0,4651	0,9252	0,9321	0,9318	0,9335	0,9317	0,9309
14	70	0,4771	0,4777				0,4774	0,4774	0,477				0,4772	0,9545	0,9547				0,9546
15	75	0,4881	0,4863				0,4872	0,4882	0,4873				0,4878	0,9763	0,9736				0,9750
16	80	0,4926	0,4954				0,4940	0,4913	0,495				0,4932	0,9839	0,9904				0,9872
17	85	0,5053	0,5069				0,5061	0,5152	0,5034				0,5093	1,0205	1,0103				1,0154

III. Analiza wyników

Rysujemy wykres zależności kwadratu wychylenia od długości l.

Następnie korzystając z metody najmniejszych kwadratów wyznaczamy współczynnik a prostej najlepszego dopasowania. Na wykresie prostą przedstawianą za pomocą linii ciągłej.

a = 3,99

Błędy wyznaczenia współczynników a i b.

Δa = 0,01

Możemy wyznaczyć teraz przyśpieszeni ziemskie. Korzystając z poniższego wzoru.

Z powyższych wzorów wynika.

g = 9,94

Korzystając teraz z metody różniczki zupełnej wyliczymy błąd wyznaczenie przyspieszania ziemskiego i długość l₀ wahadła.

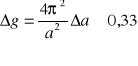
Wyniki doświadczenia:

g = 9,94 ± 0,33 m/s²

Wyznaczmy teraz wartość przyspieszenia ziemskiego uwzględniając poprawkę funkcji wynikające z funkcji f(m). Poniższa tabela przedstawia wartości funkcji f(m)

lp.	kąt	radian	F(m)
1	5	0,0873	1,000476
2	10	0,1745	1,001907
3	15	0,2618	1,004301
4	20	0,3491	1,007669
5	25	0,4363	1,012031
6	30	0,5236	1,017409
7	35	0,6109	1,023833
8	40	0,6981	1,031341
9	45	0,7854	1,039973
10	50	0,8727	1,049783
11	55	0,9599	1,060828
12	60	1,0472	1,073179
13	65	1,1345	1,086913
14	70	1,2217	1,102119
15	75	1,3090	1,118896
16	80	1,3963	1,13735
17	85	1,4835	1,157591

Postępujemy w podobny sposób jak w przypadku pierwszym.

Wykres zależności okresu wahadła od wartości funkcji kwadratu f(m).

`

f(m) dla 5^o wynosi 1,0005

a = 3,99

Błędy wyznaczenia współczynnika.

Δa = 0,01

Po podstawieniu do wzoru przyspieszenie ziemskie otrzymaliśmy następującą wartość przyspieszenia ziemskiego

g = 9,94 ± 0,34m/s²

IV. Wnioski

Otrzymana wartość przyspieszenia ziemskiego nie różni się zbytnio od tego jakie podają tablice fizyczne 9,81 m/s². Uwzględnienie poprawki kąta tylko nieznacznie przybliżyło otrzymany wynik do wartość tablicowych, Wyniki różniły się 0,13 m/s²_. Różnica ta stanowi bardzo mały procent szukanej wielkości. Po uwzględnieniu poprawki związaną z funkcją f(m) zwiększył się błąd wyznaczenia wielkość. Było to spowodowane dużą niedokładnością pomiaru kąt. Także zwiększyło się odstępstwo od wartości tablicowej gdyż wartość funkcji f(m) jest większa od jedności. Co powoduje zawyżenie wyniku.

Zawyżenie szukanej wielkości jest spowodowane oporem powietrza, drganiami statywu i nie równym puszczaniem wahadła. Wszystkie te czynniki spowodowały wzrost okresu wahadła co spowodowało sztuczne zawyżenie szukanej wielkość.

Zespół Nr 2 Politechnika Warszawska Doświadczenie Nr 6

Jarosław Bomba Wydział Fizyki

Krzysztof Drewicz

7

---