Adrian Standowicz 25.03.2009

I TM Aa

Ćwiczenie 4: Wyznaczanie logarytmicznego dekrementu tłumienia

1. WSTĘP:

1. Ruch harmoniczny prosty:

Ruch harmoniczny możemy zdefiniować jako ruch rzutu punktu materialnego, poruszającego się ruchem jednostajnym po okręgu, na średnicę tego okręgu. Mówimy, że ciało wykonuje ruch harmoniczny prosty, jeśli siła na nie działająca jest wprost proporcjonalna do jego wychylenia z położenia równowagi, ale skierowana przeciwnie do kierunku wychylenia, a wychylenia ciała opisywane są funkcją sinusoidalną zależną od czasu.

2. Siła oporu w ruchu harmonicznym:

Ruch harmoniczny tłumiony występuje wtedy, gdy na ciało działa dodatkowo siła tłumiąca (oporu) ośrodka. Niezależnie od natury ośrodka, siła tłumiąca F_t jest proporcjonalna do prędkości ciała drgającego, jeśli prędkość ta jest niewielka:

, gdzie: b - współczynnik oporu

F_t - siła tarcia ośrodka (tłumiąca)

V - prędkość

Znak „-„ we wzorze uwzględnia fakt, że siła F_t jest

zawsze skierowana przeciwnie do kierunku ruchu.

Równanie to ma dwie klasy rozwiązań:

1. Oscylator przetłumiony:
   

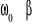
w tej sytuacji nie występuje ruch wahadłowy, a jedynie ekspotencjalny zanik wychylenia z czasem.

2. Oscylator drgający:
   

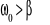
1. Drgania tłumione:

Jeżeli drgania ciała odbywaką się w ośrodku materialnym (gaz, ciecz), to wskutek występowania siły oporu ośrodka (siły tłumiącej), drgania będą zanikać.

Uwzględniając działanie tej siły, zgodnie z II zasadą dynamiki otrzymujemy:

1.
- współczynnik tłumienia

2.

3.
- pulsacja drgań tłumionych

Zależność wychylenia x przykładowego drgania tłumionego od czasu t, ukazuje

poniższy wykres:

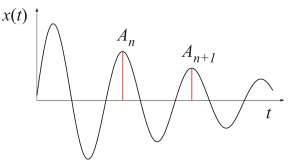
2. Logarytmiczny dekrement tłumienia:

Wielkość fizyczna charakteryzująca tłumienie drgań. Jest to logarytm naturalny stosunku amplitud dwóch kolejnych wychyleń w tę samą stronę, z których druga amplituda następuje po pierwszej po czasie równym okresowi - T.

Są to amplitudy odpowiadających chwilom t₁ = t oraz t₂ = t₁ + T. Po upływie jednego okresu (t = T) amplituda drgań maleje do A_1T=A₀·e^-βT, po upływie zaś czasu równego n okresom (t=nT) amplituda drgań maleje do A­­_nT = A₀·e^-n·βT. Otrzymujemy więc wzór:

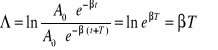
, gdzie:

- współczynnik zwany stałą tłumienia

- początkowa maksymalna amplituda

- dekrement logarytmiczny tłumienia

Łatwo się przekonać, że δ jest odwrotnością liczby drgań N, po których maksymalne wychylenie maleje e razy: δ = 1/N. Czas τ, w którym się to dzieje, nazywa się czasem relaksacji.

2. TABELE POMIAROWE:

- t = 10T - m = 361g - A₀ = 25cm

Skrzydło zamknięte:

	Czas pełnych 20 wachnięć - T20	Średnia - T20śr	Okres drgań - T
Pomiar 1	69,63 s	69,3 s	3,465 s
Pomiar 2	68,95 s
Pomiar 3	68,88 s
Pomiar 4	69,44 s
Pomiar 5	69,64 s

t (T)	t (s)	1 pomiar	2 pomiar	3 pomiar	Średnia	Ln(Aśr)
0 T	0	25	25	25	25,00	3,22
0,5 T	1,7325	24	23	22,5	23,17	3,14
1 T	3,465	22	22	22	22,00	3,09
1,5 T	5,1975	20	19,5	20	19,83	2,99
2 T	6,93	19	19	19	19,00	2,94
2,5 T	8,6625	18	17	17,5	17,50	2,86
3 T	10,395	16	17	16,5	16,50	2,80
3,5 T	12,128	16	15	15,5	15,50	2,74
4 T	13,86	15	15	14,5	14,83	2,70
4,5 T	15,593	14	14	14	14,00	2,64
5 T	17,325	13	13	13	13,00	2,56
5,5 T	19,058	12,5	12,5	12,5	12,50	2,53
6 T	20,79	12	12	12	12,00	2,48
6,5 T	22,523	11	11	11	11,00	2,40
7 T	24,255	10,5	11	10,5	10,67	2,37
7,5 T	25,988	10	10	10	10,00	2,30
8 T	27,72	9,7	9,9	9,5	9,70	2,27
8,5 T	29,453	9,5	9,5	9	9,33	2,23
9 T	31,185	9	9	8,75	8,92	2,19
9,5 T	32,918	8	8	8,5	8,17	2,10
10	34,65	8	8	8	8,00	2,08

Skrzydło otwarte:

	Czas pełnych 20 wachnięć - T20	Średnia - T20śr	Okres drgań - T
Pomiar 1:	69,24	68,9 s	3,445 s
Pomiar 2:	68,76
Pomiar 3:	69,26
Pomiar 4:	69,23
Pomiar 5:	68,88

t (T)	t (s)	1 pomiar	2 pomiar	3 pomiar	Średnia	Ln(Aśr)
0 T	0	25	25	25	25,00	3,22
0,5 T	1,7225	23	23,5	23,5	23,33	3,15
1 T	3,445	22	22,5	22	22,17	3,10
1,5 T	5,1675	21	21	21,5	21,17	3,05
2 T	6,89	20	20	20,5	20,17	3,00
2,5 T	8,6125	19	19,5	19,5	19,33	2,96
3 T	10,335	18	18,5	18,5	18,33	2,91
3,5 T	12,058	17,5	17,5	18	17,67	2,87
4 T	13,78	17	17	17	17,00	2,83
4,5 T	15,503	16	16,5	16,5	16,33	2,79
5 T	17,225	16	15,5	15,5	15,67	2,75
5,5 T	18,948	15	15	15	15,00	2,71
6 T	20,67	14,5	14	14,5	14,33	2,66
6,5 T	22,393	13,5	14	14	13,83	2,63
7 T	24,115	13,5	13	13,5	13,33	2,59
7,5 T	25,838	12,5	13	13,25	12,92	2,56
8 T	27,56	12	12,5	12,5	12,33	2,51
8,5 T	29,283	11,5	12	12	11,83	2,47
9 T	31,005	11,5	12	11,5	11,67	2,46
9,5 T	32,728	11	11,5	11,5	11,33	2,43
10	34,45	11	11	11	11,00	2,40

3. OBLICZENIA (współczynnik tłumienia β wyznaczany za pomocą regresji liniowej):

Dla skrzydła zamkniętego: Dla skrzydła otwartego:

l.p.		xi		yi		xi²		yi^2		xiyi
1		0,00		3,22		0,00		10,37		0,00
2		1,7225		3,15		2,97		9,92		5,43
3		3,445		3,10		11,87		9,61		10,68
4		5,1675		3,05		26,70		9,30		15,76
5		6,89		3,00		47,47		9,00		20,67
6		8,61256		2,96		74,18		8,76		25,49
7		10,335		2,91		106,81		8,47		30,07
8		12,058		2,87		145,40		8,24		34,61
9		13,78		2,83		189,89		8,01		39,00
10		15,503		2,79		240,34		7,78		43,25
11		17,225		2,75		296,70		7,56		47,37
12		18,948		2,71		359,03		7,34		51,35
13		20,67		2,66		427,25		7,08		54,98
14		22,393		2,63		501,45		6,92		58,89
15		24,115		2,59		581,53		6,71		62,46
16		25,838		2,56		667,60		6,55		66,15
17		27,56		2,51		759,55		6,30		69,18
18		29,283		2,47		857,49		6,10		72,33
19		31,005		2,46		961,31		6,05		76,27
20		32,728		2,43		1071,12		5,90		79,53
21		34,45		2,40		1186,80		5,76		82,68
		361,73		58,05		8515,47		161,74		946,14
l.p.	xi		yi		xi^2		yi^2		xiyi
1	0,00		3,22		0,00		10,37		0,00
2	1,7325		3,14		3,00		9,86		5,44
3	3,465		3,09		12,01		9,55		10,71
4	5,1975		2,99		27,01		8,94		15,54
5	6,93		2,94		48,02		8,64		20,37
6	8,6625		2,86		75,04		8,18		24,77
7	10,395		2,80		108,06		7,84		29,11
8	12,128		2,74		147,09		7,51		33,23
9	13,86		2,70		192,10		7,29		37,42
10	15,593		2,64		243,14		6,97		41,17
11	17,325		2,56		300,16		6,55		44,35
12	19,058		2,53		363,21		6,40		48,22
13	20,79		2,48		432,22		6,15		51,56
14	22,523		2,40		507,29		5,76		54,06
15	24,255		2,37		588,31		5,62		57,48
16	25,988		2,30		675,38		5,29		59,77
17	27,72		2,27		768,40		5,15		62,92
18	29,453		2,23		867,48		4,97		65,68
19	31,185		2,19		972,50		4,80		68,30
20	32,918		2,10		1083,59		4,41		69,13
21	34,65		2,08		1200,62		4,33		72,07
	363,83		54,63		8614,62		144,58		871,30

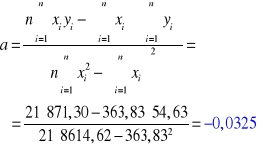
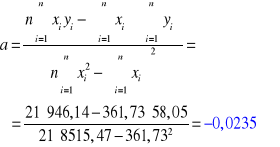
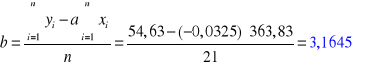
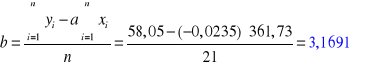
3. RACHUNEK BŁĘDU:

Błąd wyznaczonych wartości liczb a i b:

Skrzydło zamknięte: Skrzydło otwarte:

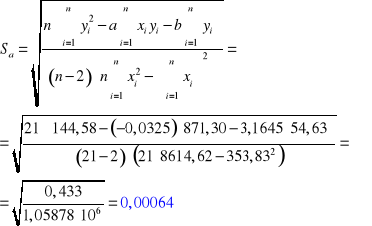
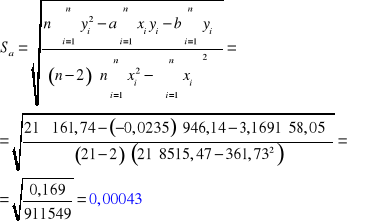
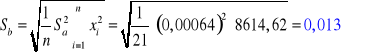
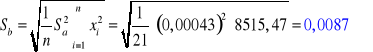
5. WNIOSKI:

Ćwiczenie to pozwoliło nam na poznanie zjawiska oporu powietrza i jego wpływu na ruch harmoniczny prosty. Zarówno przy skrzydle zamkniętym, jak i otwartym, wahadło wykonuje drgania tłumione. Oczywiście tłumienie zależne jest od wielkości powierzchni stawiającej opór (im większa powierzchnia tym większy opór) oraz prędkości z jaką porusza się ciało (im większa tym większy opór), co widać wyraźnie w tabelach pomiarowych.

Logarytmiczny dekrement tłumienia określa nam jak gwałtownie spada amplituda drgań w przeciągu jednego okresu T. W naszym przypadku, gdybyśmy określali logarytmiczny dekrement tłumienia dla każdej wartości średniej odchyleń, w miarę oscylowania wahadła wokół punktu 0, spadałby on, co oznaczałoby że stosunek dwóch kolejnych amplitud tego drgania nie jest stały w czasie. Założenie dla ruchu harmonicznego tłumionego przyjmuje jednak coś innego… Dekrement powinien być stały w czasie. Błąd ten, jak i innego typu błędy mogą wynikać z przyczyn takich, jak:

- niedokładny pomiar odchyleń

- niedokładny pomiar długości okresu T

- wykonywanie przez wahadło dodatkowych drgań poprzecznych mogących

przekłamać niektóre odczyty

itp.

SPRAWOZDANIE

---