Miłosz Piwowarczyk 2002/2003

Wydział Metali Nieżelaznych

Gr. Metalurgia

Ćwiczenie nr 10.

Temat: Współczynnik podziału - prawo Nernsta

Zespół 10

1. Wstęp teoretyczny:

Substancja rozpuszczana w dwóch pozostających w równowadze za sobą fazach (np. dwie nie mieszające się ze sobą ciecze) ulega rozdziałowi pomiędzy te fazy. W określonej temperaturze stosunek stężeń tej substancji w obydwu fazach jest wielkością stałą. Jest to prawo podziału i prawo Nernsta. Można je zapisać:

(1)

gdzie: r jest współczynnikiem podziału

Prawo podziału Nernsta stosuje się w tej formie w roztworach rozcieńczonych, w przypadku gdy stan cząstkowy substancji jest jednakowy w obydwu fazach. Jednak może wystąpić przypadek substancji, która w jednej z faz ulega silnej asocjacji, a w drugiej zaś pozostaje w stanie zdysocjowanym. W takim przypadku w każdej z faz ustala się równowaga asocjacyjno-dysacjacyjna. Zakładając w fazie I silne przesunięcia równowagi w kierunku dysocjacji w fazie II można napisać w przybliżeniu:

C_{A n I} ≈ C_II oraz C_{A II} ≈ C _II

nA An Faza I

nA An Faza II

Gdzie C_I oraz C_II oznaczają analityczne określenia stężenia substancji bez uwzględnienia asocjacji i dysocjacji. Stany równowagi w poszczególnych fazach charakteryzują odpowiednie stałe

(2)

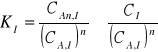
(3)

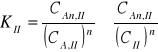
Gdy Substancja rozpuszczona ulega częściowej dysocjacji lub asocjacji prawo podziału zachowuje ważność dla ułamka substancji występującej w tym samym stanie cząsteczkowym w obydwu fazach

(4)

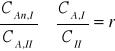
Dążymy do zastąpienia w równaniu (4) trudnej do wyznaczenia doświadczalnego wartości C_A,I, przez łatwą do analitycznego wyznaczenia wartości C_I. W tym celu przekształca się równanie (2)

(5)

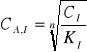
Wstawiając równanie (5) do (4) otrzymujemy:

(6)

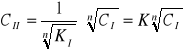
Lub w dogodnej dla doświadczalnego wyznaczenia postaci:

(7)

2. Cel ćwiczenia:

Celem ćwiczenia jest doświadczalne wyznaczenie współczynnika podziału kwasu octowego pomiędzy wodę i butanol oraz sprawdzenie, czy w obydwu fazach kwas benzoesowy występuje w tym samym stanie cząsteczkowym, a jeżeli nie to w jakiej postaci cząsteczkowej rozpuszcza się w poszczególnych fazach.

3. Oblicznia:

Wyniki oznaczeń współczynnika podziału kwasu octowego między wodę i alkohol butylowy NaOH 0,1n V = 5ml						c but [mol/l]	współczynnik podziału r
Nr próbki	c kwasu [mol/l]	obj. NaOH [ml]			c roztworu wodnego [mol/l]
				1				2	średnia
1	0,05	1,1	1,2	1,15	0,023	0,027	0,852
2	0,1	2,1	2,1	2,1	0,042	0,058	0,724
3	0,25	5,5	5,6	5,55	0,111	0,139	0,799
4	0,5	11,4	11,5	11,45	0,229	0,271	0,845
5	0,75	17,2	17,1	17,15	0,343	0,407	0,843
6	1	23,9	23,5	23,7	0,474	0,526	0,901
						średni:	0,827

Wykres zależności C_w = f(C_b)

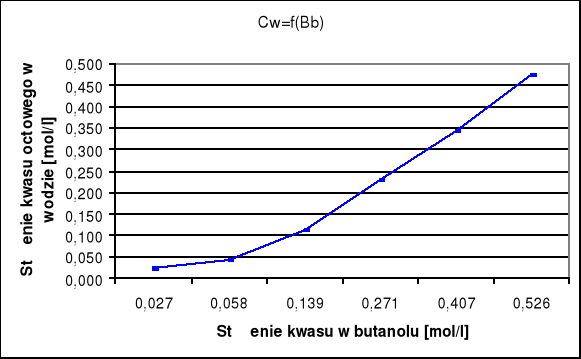
Z analizy wynika że zależność stężenia kwasu octowego w wodzie, od stężenia w butanolu jest zależnością liniową. Dla dużych rozcieńczeń jednak możemy zaobserwować odstępstwo od tego - wynikać to może z niedokładnego zmiareczkowania jak i błędu rozcieńczenia. Średnia wartość C_w/C_b dla naszego doświadczenia wynosi 0,827.

Obliczenia dla serii Nernsta i Smitha:

Stężenia kwasu benzoesowego w będących ze sobą w równowadze roztworach wodnych i benzenowych
Stężenia w wodzie Cw		log Cw	Stężenie w benzenie Cb		log Cb
[mol/l]* 10^3	[g/l]			[mol/l]* 10^3		[g/l]
Wyniki Nernsta otrzymane w t^0 = 20^0C
1,34	0,163	0,126	4,385	0,535	0,642
2,00	0,244	0,301	8,115	0,99	0,909
3,70	0,452	0,569	22,377	2,73	1,350
6,46	0,788	0,810	60,410	7,37	1,781
12,30	1,5	1,090	198,361	24,2	2,297
23,69	2,89	1,375	795,082	97	2,900
Wyniki Smitha otrzymane w t^0 = 25^0C
0,8725	0,106	-0,059	1,525	0,186	0,183
0,925	0,113	-0,034	1,95	0,238	0,290
1,3	0,159	0,114	3,45	0,421	0,538
1,725	0,210	0,237	5,5	0,671	0,740
2,8	0,342	0,447	11,9	1,452	1,076
4	0,488	0,602	19,75	2,410	1,296

Wykresy zależności C_w = f (C_b):

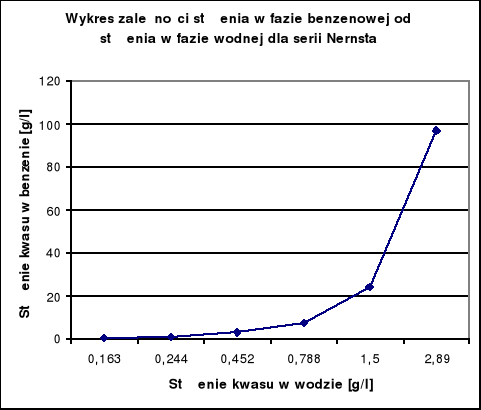
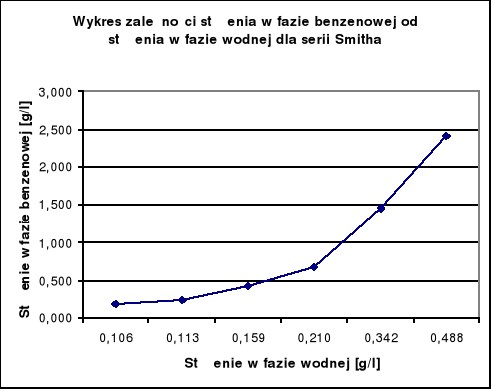
Wykresy te nie są liniowe czyli istnieje różnica stanu cząsteczkowego w obydwu fazach. W związku z tym sporządzam wykresy log c_w = f (log c_b) dla wyników Nernsta i Smitha.

Wykresy zależności log C_w = f (log C­_b):

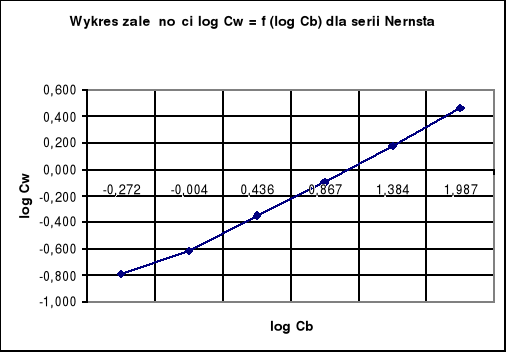
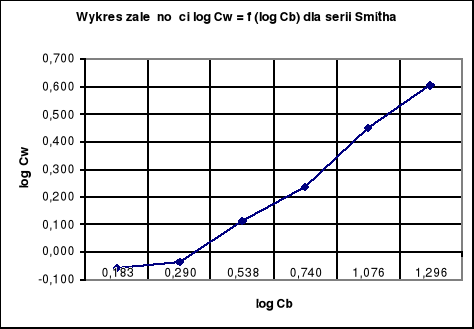
Wykresy log c_w = f (log c_b) dla wyników Nernsta i Smitha - obydwie zależności po zlogarytmizowaniu są liniowe, czyli możemy zastosować wzór
i obliczyć liczbę „n” cząstek tworzących kompleks (C₆H₅COOH)_n dla obydwu przypadków.

Obliczanie wartości „n” dla serii Nernsta.

n=1,924 ≈ 2

Obliczanie wartości „n” dla serii Smitha:

n = 1,883 ≈ 2

4. Wnioski:

Pierwsza część doświadczenia udowodniła słuszność prawa Nernsta wykresy zależności C_w = f (C_b) są liniowe, a średni współczynnik podziału C_w/C_b wynosi 0,894 .

Dla wyników pomiarów Nernsta i Smitha zależność ta ma charakter nieliniowy. Liniowość otrzymujemy dopiero po zlogarytmizowaniu danych. Na podstawie naszych obliczeń możemy stwierdzić że badane substancje nie były w tym samym stanie cząsteczkowym. Więc z przeprowadzonych obliczeń możemy przypuszczać że utworzył się związek kompleksowy (C₆H₅COOH)₂ .

---