Wydział IMiC	Wykonujący: Maciej Skrzypek Przemysław Pudlik Michał Proć	Rok II		Grupa 6	Zespół A
Laboratorium Chemii Fizycznej	TEMAT: Katalityczny rozkład wody utlenionej				Ćwiczenie: 10
Data wykonania:	Data oddania:		Data zaliczenia:		Ocena:

1. Cel ćwiczenia.

Celem ćwiczenia jest wyznaczenie stałej szybkości reakcji rozkładu wody H₂O₂ w obecności różnych ilości katalizatora (MnO₂) oraz w roztworze bez katalizatora.

2. Przyrządy i odczynniki.

Do ćwiczenia wykorzystano:

• 30% roztwór H₂O₂ (perhydrol)

• bufor boranowy

• 1M H₂SO₄

• 0,02M KMnO₄

• Szkło laboratoryjne (erlenmajerki, pipety o różnej objętości, kolba miarowa 50cm³)

3. Wykonanie ćwiczenia.

Do kolby miarowej 50 cm³ wlać 10 cm³ perhydrolu (30% wag. Roztwór H₂O₂) i dopełnić do kreski wodą destylowaną.

Do czterech kolb wlać:

• 100 cm³ wody destylowanej

• 30 cm³ buforu boranowego (0,2M H₃BO₃ i 0,05M Na₂B₄O₇ w stosunku 9:1 w sumie dający ilość 120 cm³)

• 5 cm³ roztworu H₂O₂ przygotowanego wcześniej

• roztwór KMnO₄ o stężeniu 0,02M jako katalizator w ilości (1-10 cm³, 2-8 cm³,

3-5 cm³, 4-0 cm³)

Miareczkowanie:

Do erlenmajerki dodać 10 cm³ roztworu przygotowanego wcześniej oraz 2 cm³ 1M H₂SO₄.

Miareczkowanie wykonywać w przedziale czasowym:

• co 5 min. przez 30 min.

• co 5 min. przez 30 min.

• co 5 min. przez 40 min.

• co 20 min. przez 120 min.

4. Opracowanie wyników:

Wyniki miareczkowań zebrano w tabelach poniżej.

Tabela1

Objętość roztworu katalizatora [cm^3]	czas	VKMnO4 [cm^3]	ln VKMnO4
				t [min]
	10	0	6,3	1,84
		5	2,9	1,06
		10	1,5	0,41
		15	0,7	-0,36
		20	0,4	-0,92
		25	0,2	-1,61
		30	0,1	-2,30

Tabela 2

Objętość roztworu katalizatora [cm^3]	czas	VKMnO4 [cm^3]	ln VKMnO4
				t [min]
	8	0	12,3	2,51
		5	5,2	1,65
		10	2,2	0,79
		15	0,9	-0,11
		20	0,4	-0,92
		25	0,2	-1,61
		30	0,1	-2,30

Tabela 3

Objętość roztworu katalizatora [cm^3]		VKMnO4 [cm^3]	ln VKMnO4
				czas
				t [min]
	5	0	11,4	2,43
		5	9,2	2,22
		10	7,2	1,97
		15	5,9	1,77
		20	4,4	1,48
		25	3,4	1,22
		30	2,6	0,96
		35	1,8	0,59
		40	1,3	0,26

Tabela 4

Objętość roztworu katalizatora [cm^3]		VKMnO4 [cm^3]	ln VKMnO4
				czas t [min]
	0	0	13,4	2,60
		20	13,3	2,59
		40	13,2	2,58
		60	13,2	2,58
		80	13,1	2,57
		100	13,1	2,57
		120	13	2,56

Na podstawie tych wyników sporządziliśmy wykres zależności ln(VKMnO₄) od czasu:

Rys 1.

Stałe szybkości reakcji k wyznaczone z nachylenia wykresów (a= -k):

roztwór z 10 cm³ KMnO₄: y = -0,136x + 1,778

roztwór z 8 cm³ KMnO₄: y = -0,161x + 2,429

roztwór z 5 cm³ KMnO₄: y = -0,053x + 2,512

roztwór z 0 cm³ KMnO₄: y = -0,00023x + 2,593

Jako że jest to reakcja rzędu pierwszego więc τ ½ możemy obliczyć ze wzoru:

τ ½
(1)

Czasy połowicznej przemiany τ ½ dla kolejnych roztworów:

roztwór	Vkat [cm^3]	k[1/min.]	τ½ [min.]
I	10	0,136	5,10
II	8	0,161	4,31
III	5	0,053	13,08
IV	0	0,00023	3013,68

Następnie sporządziliśmy wykres zależności objętości KMnO₄ od ilości katalizatora po 20 minutach:

Rys 2.

Następnie sporządziliśmy wykres zależności stałej szybkości reakcji od ilości katalizatora:

Rys. 3.

Wyniki obliczeń stężenia H₂O₂ zebrano w poniższych tabelach:

(2)

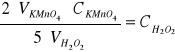
(3)

Tabela 5

Objętość rotworu katalizatora [cm^3]	czas	VKMnO4 [cm^3]	C H2O2 [mol/dm^3]
				t [min]
	10	0	6,3	0,01008
		5	2,9	0,00464
		10	1,5	0,00240
		15	0,7	0,00112
		20	0,4	0,00064
		25	0,2	0,00032
		30	0,1	0,00016

Tabela 6

Objętość rotworu katalizatora [cm^3]	czas	VKMnO4 [cm^3]	C H2O2 [mol/dm^3]
				t [min]
	8	0	12,3	0,01968
		5	5,2	0,00832
		10	2,2	0,00352
		15	0,9	0,00144
		20	0,4	0,00064
		25	0,2	0,00032
		30	0,1	0,00016

Tabela 7

Objętość rotworu katalizatora [cm^3]		VKMnO4 [cm^3]
			czas		C H2O2 [mol/dm^3]
			t [min]
	5	0	11,4	0,01824
		5	9,2	0,01472
		10	7,2	0,01152
		15	5,9	0,00944
		20	4,4	0,00704
		25	3,4	0,00544
		30	2,6	0,00416
		35	1,8	0,00288
		40	1,3	0,00208

Tabela 8

Objętość rotworu katalizatora [cm^3]		VKMnO4 [cm^3]	C H2O2 [mol/dm^3]
				czas t [min]
	0	0	13,4	0,02144
		20	13,3	0,02128
		40	13,2	0,02112
		60	13,2	0,02112
		80	13,1	0,02096
		100	13,1	0,02096
		120	13	0,02080

Następnie sporządziliśmy wykresy zależności objętości KMnO_{4 od} stężenia H₂O₂ :

Rys 4.

Rys 5

Rys 6

Rys 7

Ostatnią czynnością było sporządzenie wykresu zależności stężenia H₂O₂ od czasu:

Rys 8

Wnioski:

Rysunek 1.

Przedstawia zależność ln(V KMnO₄) od czasu. Jak widzimy dla roztworu bez dodatku katalizatora wykres przyjmuje wartość stałą oscylującą wokół 3. Natomiast dla innych roztworów mamy do czynienia z funkcją malejącą.

Rysunek 2.

Przedstawia zależność użytego podczas miareczkowania KMnO₄ od ilości katalizatora po czasie 20 minut.

Rysunek 3.

Przedstawia zależność stałej szybkości reakcji od ilości katalizatora. Jak widzimy wraz ze wzrostem ilości dodanego katalizatora stała szybkości reakcji wzrasta, co świadczy o tym że katalizator zwiększa szybkość reakcji, w przypadku 8 cm3 katalizatora obserwujemy odstępstwo od tego i stała szybkości tej reakcji jest większa niż dla 10 cm3. Należy również zauważyć że wraz ze wzrostem stałej szybkości reakcji maleje czas połowicznego rozpadu.

Rysunki 4,5,6,7.

Przedstawiają zależność objętości KMnO₄ stężenia H₂O₂. Jak widzimy wszystkie wykresy są zależnościami liniowymi w których wraz ze wzrostem stężenia H₂O₂ wzrasta objętość KMnO_4.

Rysunek 8.

Ostatni wykres przedstawia zależność stężenia H₂O₂ od czasu. Jak widzimy dla roztworów z dodatkiem katalizatora stężenie spada wraz z czasem, natomiast dla roztworu bez dodatku katalizatora pozostaje praktycznie bez zmian.

---